Презентация на тему: Решение неравенств с одной переменной 11 класс

Решение неравенств с одной переменной Муниципальное бюджетное общеобразовательное учреждение средняя общеобразовательная школа №30 имени А.И.Колдунова

Цели: развитие логического мышления формируя умения и навыки решения систем и совокупностей неравенств, выполняя равносильные переходы; развитие умения кратко отвечать на вопрос и ставить его; развитие учебно-коммуникативных умений при работе в группе (слушать, аргументировать, доходчиво объяснять); развитие умений работать во времени; развитие навыков самостоятельной деятельности и самоконтроля.

Определение Таким образом, два неравенства являются равносильными на множестве Х, если множества решений этих неравенств совпадают.

Поэтому вместо того чтобы решать данное неравенство, можно решать любое другое, равносильное данному.

Важно понимать, что для доказательства неравносильности двух неравенств нет необходимости решать каждое из неравенств, а затем убеждаться в том, что множества их решений не совпадают – достаточно указать одно решение одного из неравенств, которое не является решением другого неравенства.

Пусть функции f(x), g(x), h(x) определены на множестве Х. Тогда справедливы следующие равносильные переходы:

Системы и совокупности неравенств

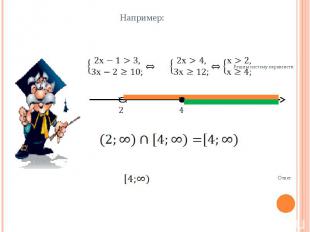
Например:

Определение. Несколько неравенств с одной переменной образуют совокупность неравенств, если ставится задача найти все такие значения переменной, каждое из которых является хотя бы одного из заданных неравенств. Каждое такое значение переменной называют частным решением совокупности неравенств. Множество всех частных решений совокупности неравенств представляет собой решение совокупности неравенств.

Например

Задание группам

Домашнее задание №№ 57.4б, 57.5б, 57.8б.

Самостоятельная работа 1 вариант №№ 57.6а, 57.7а, 57.9а.