Презентация на тему: Решение неравенств первой степени с одной переменной

Урок алгебры в 8 классе Автор: учитель муниципальной Бородинской средней общеобразовательной школы Малкова Ирина Александровна

Тема: решение неравенств первой степени с одной переменной (графический способ решения) ах + в > o cх + d < в ах + в ≤ cх + d

Цели урока:Повторить свойства числовых неравенств, научиться решать эти неравенства графическим способом, закрепить полученные знания на практической работе;развитие математи-ческого кругозора, логического мышления, культуры речи;воспитание интереса к математике. Оборудование:Планшетки с координатной плоскостью;фломастеры, мелки разных цветов, линейки;компьютеры.

Устный счет – зарядка для ума. На основании каких свойств числовых неравенств можно утверждать: если х > у, то 15х > 15у -9х < -9у х + 20 > у + 20 х > у 3 3Известно, что а > в. Верно ли, что а + 5 > в + 4, а + 3 > в + 6а > в, что можно сказать о разности а – в, Сравнить а и в, если разность в - а < 0

Актуализация знаний Решить данные неравенства (с объяснением свойств, используемых при решении), на числовой прямой указать решение и записать ответ числовым промежутком: а) 2х + 6 > 0, в) х + 4 < 6, с) 4х – 7 > х - 4.Этапы графического решения уравнений.Построение графиков линейных функций вида: а) у = 0; в) у = с; с) у = kх + b; d) y =kx + d у у = kx+b у = с b х у = 0 d y = kx+d

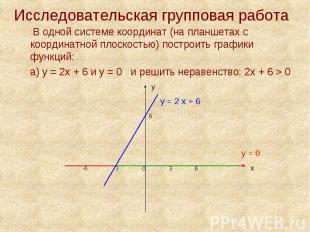
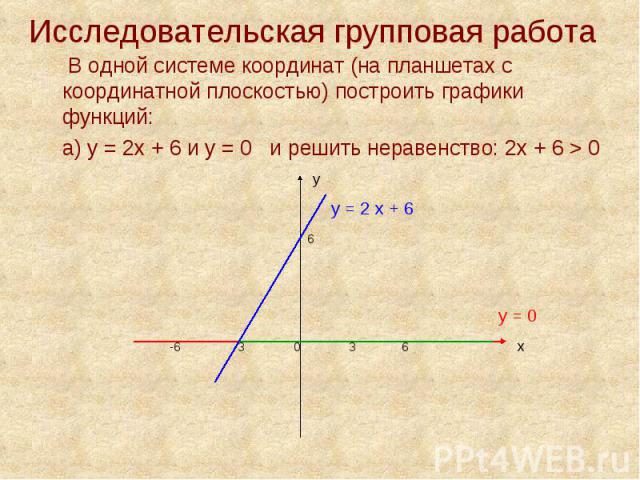
Исследовательская групповая работа В одной системе координат (на планшетах с координатной плоскостью) построить графики функций: а) у = 2х + 6 и у = 0 и решить неравенство: 2х + 6 > 0 у у = 2 х + 6 6 у = 0 -6 -3 0 3 6 х

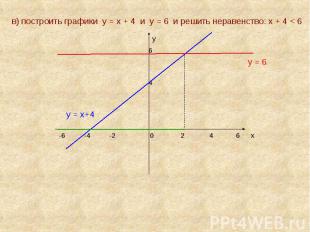
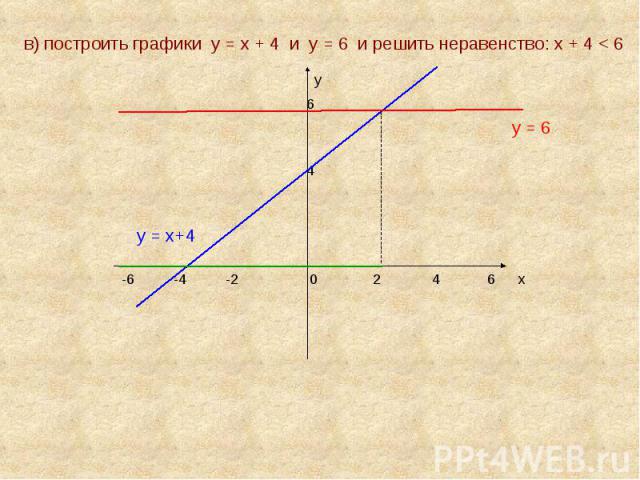
в) построить графики у = х + 4 и у = 6 и решить неравенство: х + 4 < 6

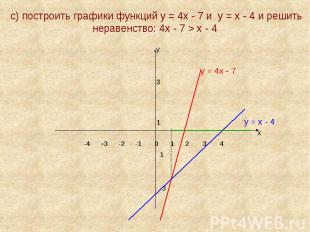
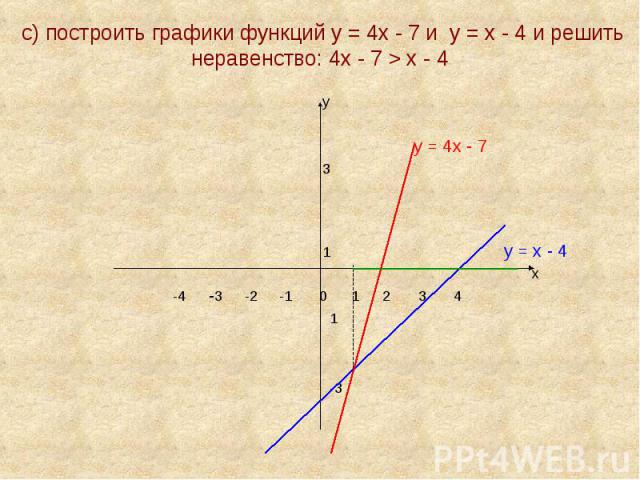
с) построить графики функций у = 4х - 7 и у = х - 4 и решить неравенство: 4х - 7 > х - 4

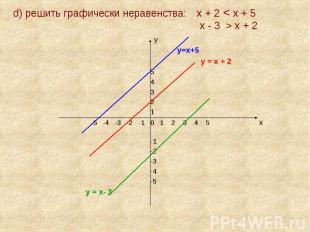
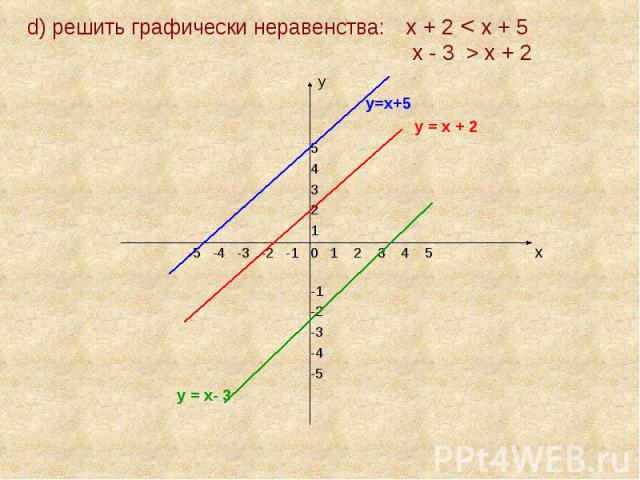
d) решить графически неравенства: х + 2 < х + 5 х - 3 > х + 2

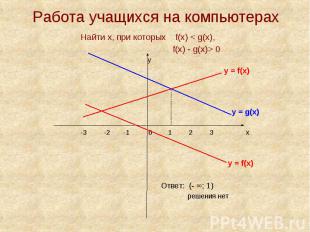
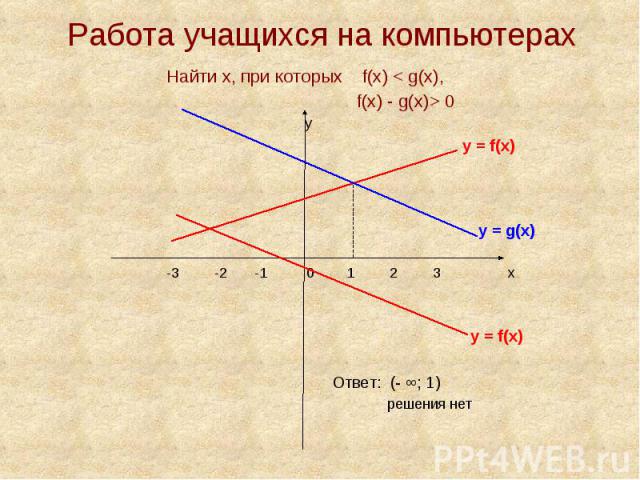
Работа учащихся на компьютерах Найти х, при которых f(х) < g(х), f(х) - g(х)> 0 у у = f(х) у = g(х)-3 -2 -1 0 1 2 3 х у = f(х) Ответ: (- ∞; 1) решения нет

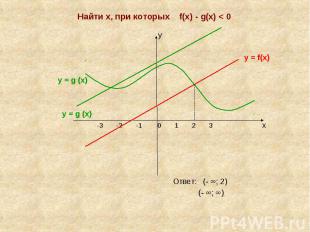
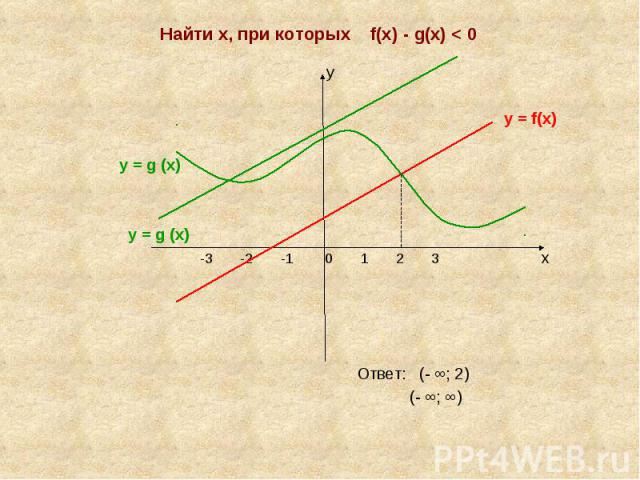
Найти х, при которых f(х) - g(х) < 0

Итог урока Повторили: свойства числовых неравенств, этапы решения неравенств первой степени, способы записи решений этих неравенств, построение графиков линейных функций;Научились решать неравенства первой степени графическим способом;Пробовали применять на практике полученные на уроке знания.

Домашнее задание Проверить степень усвоения темы: «Графический способ решения неравенств первой степени» вы сможете , выполнив дома предложенный вам тест (каждый ребенок получает задание на карточках). Спасибо за урок!