Презентация на тему: Первообразная и интеграл

`Первообразная и интеграл

Исторические сведения Интегральное исчисление возникло из потребности создать общий метод Разыскания площадей , объемов и центров тяжести. В зародышевой форме такой метод применялся ещё Архимедом . Систе-Матическое развитие он получил в 17-м веке в работах Кавальери ,Торриче-лли, Фермам,Паскаля. В 1659 г. И.Барроу установил связь мемжду задачей о разыскании площади и задачей о разыскании касательной. Ньютон и Лейб-Ниц в 70-х годах 17-го века отвлекли эту связь от упомянутых частных геомет-Рических задач. Тем мсамым была установлена связь между интегральным иДифференциальным исчислением. Эта связь была использована Ньютоном , Лейбницем и их учениками дляРазвития техники интегрирования. Своего нынешнего состояния методы интег-Рирования в основном достигли в работах Л.Эйлера. Труды М.В.Остроградско-Го и П.Л.Чебышева завершили развитие этих методов.

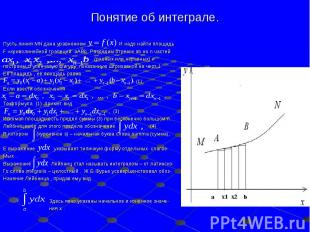
Понятие об интеграле. Пусть линия MN дана уравнением И надо найти площадьF «криволинейной трапеции aABb. Разделим отрезок ab на n частей (равных или неравных) и построим ступенчатую фигуру, показанную штриховкой на черт.1 Её площадь , её площадь равна (1)Если ввести обозначенияТо формула (1) примет вид (3)Искомая площадь есть предел суммы (3) при бесконечно большом n.Лейбниц ввёл для этого предела обозначение (4)В котором (курсивное s) – начальная буква слова summa (сумма),Е выражение указывает типичную форму отдельных слагае-Мых .Выражение Лейбниц стал называть интегралом – от латинско-Го слова integralis – целостный . Ж.Б.Фурье усовершенствовал обоз-Начение Лейбница , придав ему вид Здесь явно указаны начальное и конечное значе- ния x .

Связь между интегрированиеми дифференцированием. Будем считать а постоянной , а b – переменной величиной.Тогда интеграл будет функцией от b .Дифференциал этой функции равен

Первообразная функция. Пусть функция есть производная от функции ,Т.С. Есть дифференциал функции :Тогда функция называется первообразной для функции

Пример нахождения первообразной. Функция есть первообразная от Т.С. Есть дифференциал функции Функция является первообразной для функции

Неопределённый интеграл. Неопределённым интегралом данного выражения Называется наиболее общий вид его первообразной функции.Неопределённый интеграл выраженияобозначается Выражение называется подинтегральным выражением,Функция -подинтегральной функцией , переменная x –перемен-Ной интегрирования. Разыскание неопределённого интеграла даннойФункции называется интегрированием.

Пример нахождения неопределённого интеграла. Наиболее общий вид первообразной функции для выражения есть . Эта функция является Неопределённым интегралом выражения :Где .

Неопределённые интегралов оттригонометрических функций.

Неопределённые интегралы от некоторых функций.