Презентация на тему: Тригонометрические формулы

Урок по теме: “Тригонометрические формулы.” Ельцова Н.Г.,учитель МОУ «Гимназия №11», Г Норильск.

Рассмотрим следующие вопросы: радианная мера угла; поворот точки вокруг начала координат; определение синуса, косинуса и тангенса произвольного угла; знаки синуса, косинуса и тангенса; зависимость между синусом, косинусом и тангенсом одного и того же угла; cинус, косинус и тангенс углов и - ;

Повторим основные понятия: координатная прямая; координатная плоскость; центральный угол; sin α, cos α, где 0

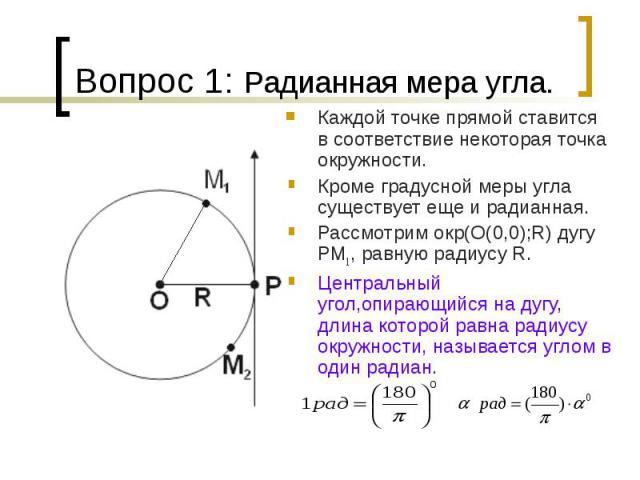
Вопрос 1: Радианная мера угла.Каждой точке прямой ставится в соответствие некоторая точка окружности. Кроме градусной меры угла существует еще и радианная. Рассмотрим окр(О(0,0);R) дугу PM1, равную радиусу R. Центральный угол,опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.

Задачи.Найти градусную меру угла,равного Найти радианную меру угла, равного

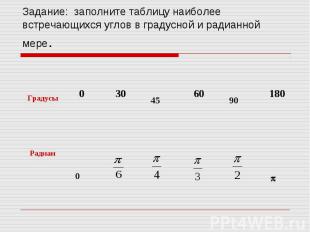
Задание: заполните таблицу наиболее встречающихся углов в градусной и радианной мере.

Вопрос 2: Поворот точки вокруг начала координат.Установим соответствие между действительными числами и точками окружности с помощью поворота точки окружности. Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота окружности вокруг начала координат на угол в a радиан, - любое действительное число. 3. Поворот на 0 радиан, означает, что точка остается на месте.

Вопрос 3: определение синуса, косинуса, тангенса угла.Синусом угла называется ордината точки, полученной поворотом точки (1,0) вокруг начала координат на угол α. Обозначается sin α Косинусом угла называется абсцисса точки, полученной поворотом точки (1,0) вокруг начала координат на угол α. При повороте т.P(1,0) на угол α, т.е на угол 90 , получается точка (0,1). Ордината точки равна 1, поэтому sin 90=sin =1. Абсцисса точки равна 0, cos90 =cos =0

Задание: Найти cos 270 = sin 270 = sin +sin1,5 = sin3 - cos1,5 =

Определение тангенса и котангенса углаТангенсом угла называется отношение синуса угла к его косинусу. tg = Котангенсом угла называется отношение косинуса угла к его синусу. ctg = Найдите tg 0°= ctg 270° = tg 0°-tq180°=

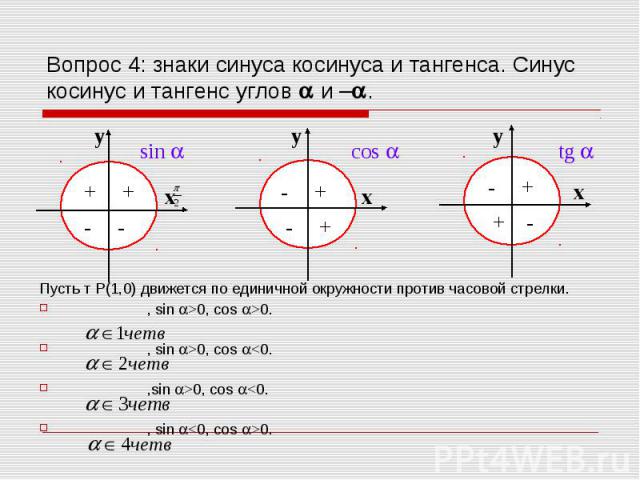
Вопрос 4: знаки синуса косинуса и тангенса. Синус косинус и тангенс углов и – .Пусть т Р(1,0) движется по единичной окружности против часовой стрелки. , sin >0, cos >0. , sin >0, cos 0, cos

Вопрос 5: Синус косинус и тангенс углов и – .Пусть т M1 и тM2 единичной окружности получены поворотом т P (1,0) на углы и – . Тогда ось Ох делит угол М1OM2пополам, поэтому тM1 и M2 симметричны относительно оси Ох М1 (cos , sin ), M2 (cos (- ), sin( )). Значит (1) sin(- )=-sin (2) cos(- )=cos Используя определения тангенса и котангенса (3) tg (- )=tg (4) ctg (- )= -ctg Формулы 1-2 справедливы при любых . Формула 3, при

Задание: 1) докажите формулу (3) самостоятельно. 2) выясните знаки синуса, косинуса и тангенса углов:а) , б) 745°, в)-

Вопрос 5 зависимость между синусом, косинусом и тангенсом одного и того же угла.Пусть т М (x;y) единичной окружности получена поворотом точки(1;0) на угол . Тогда по определению синуса и косинуса x=cos , y= sin . Точка М принадлежит единичной окружности, поэтому ее координаты удовлетворяют уравнению:х2+у2=1, следовательно sin2 +cos2 =1. (1) Равенство (1) выполняется при любых значениях и называется основным тригонометрическим тождеством. Зависимость между тангенсом и котангенсом определяется равенством: (2) tg · ctg =1,

ЗАДАЧА Дано: Найти: sin Дано: tg = 13 Найти: ctg Решение: tg ·ctg =1, следовательно ctg =

Итог урока: Чему равна радианная мера угла, градусная мера угла? Какой угол называется углом в один радиан? Что называют синусом, косинусом, тангенсом произвольного угла ? Каким равенством определяется зависимость между синусом и косинусом одного и того же угла? Как называется это равенство? Каким равенством определяется зависимость между тангенсом и котангенсом одного и того же угла?

Математический диктант. 1вариант 1. Найдите радианную меру угла. 2 вариант 40º 1500 ответ: ответ: 2. Найдите градусную меру угла ответ: ответ: 3.найдите координаты точки, полученной поворотом т(1,0) единичной окружности на угол ответ: ответ:

1вариант. 4.вычислите: 2 вариант. 1) cos00+3sin 900= 1) cos1800+5sin900= =1+3·1=1 =-1+5·1=5 2) sin 2700-2cos 1800= 2) sin1800-3cos00= =-1+2=1 =0-3=-3 3) 1+ctg2700-5tg3600= 3) sin600+cos300= =1+0+0=1 4) sin300+cos600= 4)tg3600-2ctg2700+3= =0- 0+3=3