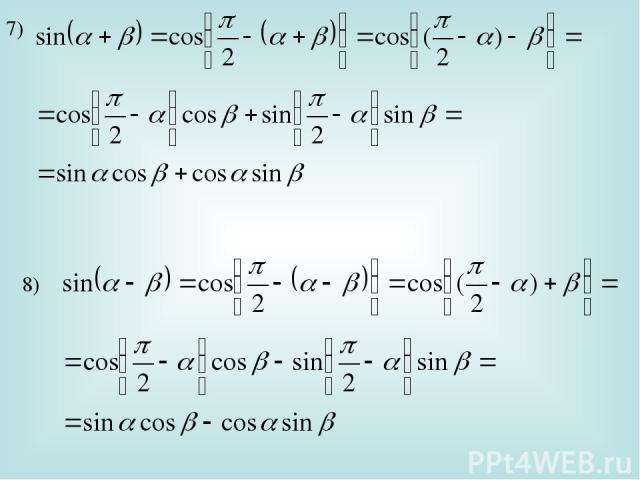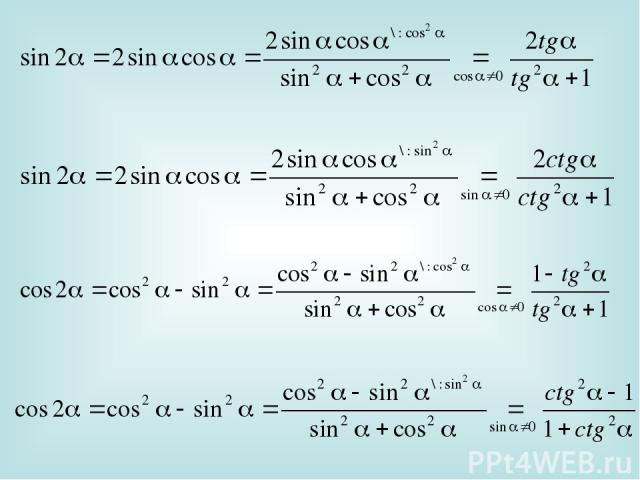Презентация на тему: Тригонометрические формулы

Государственное Образовательное Учреждение Лицей №1523 ЮАО г.Москва Лекции по алгебре и началам анализа 10 класс © Хомутова Лариса Юрьевна 900igr.net

Преобразование тригонометрических выражений (вывод тригонометрических формул)

I-a. Формулы приведения Выведем вспомогательные формулы, позволяющие находить и по тригонометрическим функциям угла .
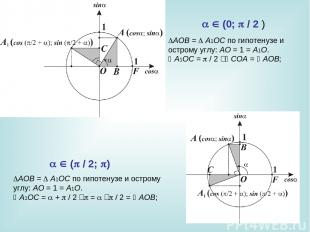
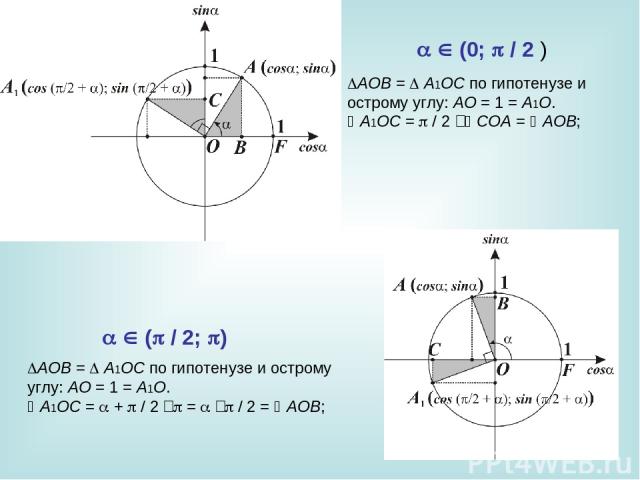
AOB = A1OC по гипотенузе и острому углу: AO = 1 = A1O. A1OC = / 2 ‑ COA = AOB; AOB = A1OC по гипотенузе и острому углу: AO = 1 = A1O. A1OC = + / 2 ‑ = ‑ / 2 = AOB; (0; / 2 ) ( / 2; )
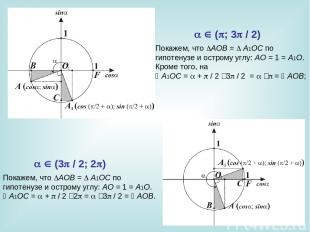
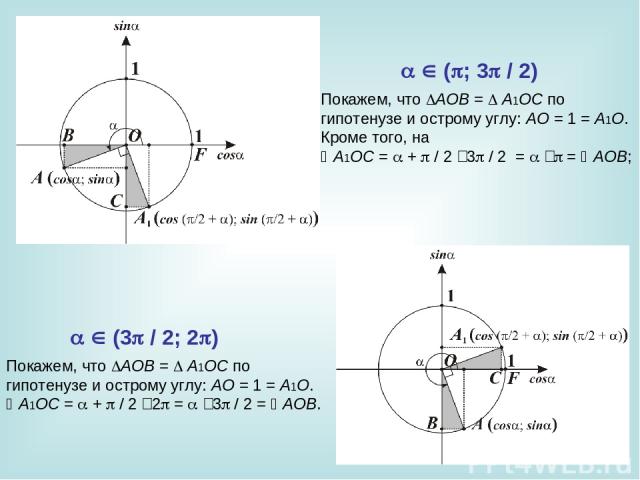
Покажем, что AOB = A1OC по гипотенузе и острому углу: AO = 1 = A1O. Кроме того, на A1OC = + / 2 ‑ 3 / 2 = ‑ = AOB; Покажем, что AOB = A1OC по гипотенузе и острому углу: AO = 1 = A1O. A1OC = + / 2 ‑ 2 = ‑ 3 / 2 = AOB. ( ; 3 / 2) (3 / 2; 2 )

, . I-a. Формулы приведения

II. Формулы сложения 0

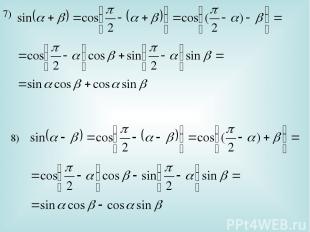

II. Формулы сложения


II. Формулы сложения
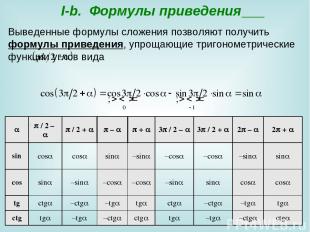
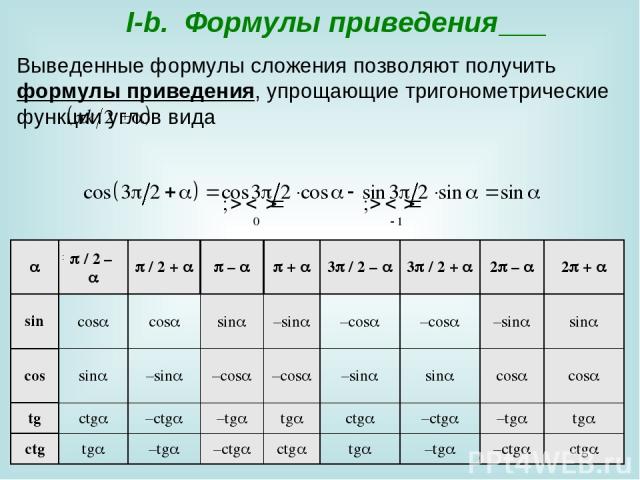
I-b. Формулы приведения Выведенные формулы сложения позволяют получить формулы приведения, упрощающие тригонометрические функции углов вида : / 2 – / 2 + – + 3 / 2 – 3 / 2 + 2 – 2 + sin cos cos sin –sin –cos –cos –sin sin cos sin –sin –cos –cos –sin sin cos cos tg ctg –ctg –tg tg ctg –ctg –tg tg ctg tg –tg –ctg ctg tg –tg –ctg ctg

III. Формулы двойных углов Чтобы вывести формулы для вычисления тригонометрических функций двойного аргумента, подставим = в формулы сложения:

III. Формулы двойных углов

III. Формулы двойных углов
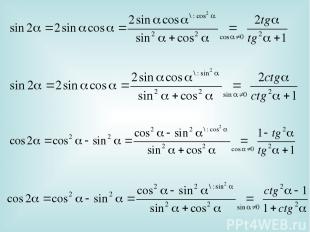

III. Формулы двойных углов

. IV. Формулы тройных углов
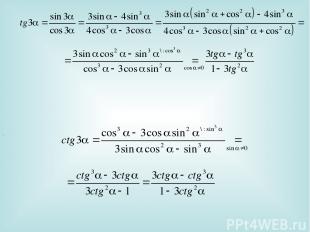
.

IV. Формулы тройных углов

V. Формулы половинных углов . .

;

V. Формулы половинных углов , . , .

VI. Формулы преобразования произведения тригонометрических функций в сумму . Сложив почленно равенства (3) и (4), получим: . Вычтя из равенства (4) равенство (3), получим: .

VI. Формулы преобразования произведения тригонометрических функций в сумму

VII. Формулы преобразования суммы тригонометрических функций в произведение .

. .

VII. Формулы преобразования суммы тригонометрических функций в произведение