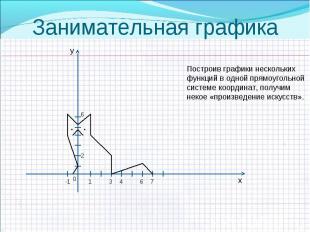
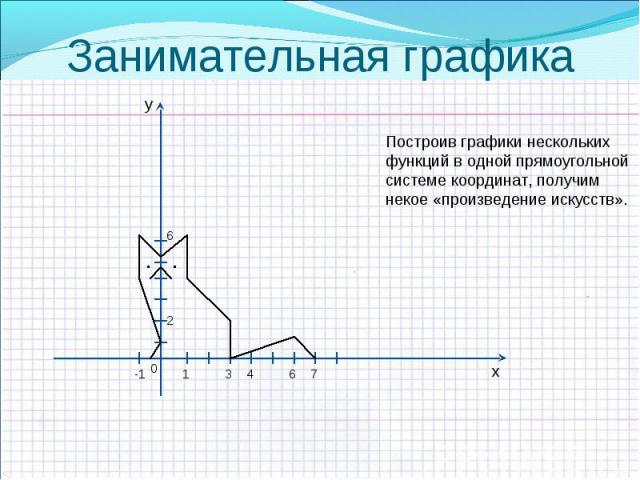
Презентация на тему: Построение графиков функций, содержащих выражения под знаком модуля

построение графиков графики функций, содержащие выражения под знаком модуля построение графиков графики функций, содержащие выражения под знаком модуля

1) построить график функции, опустив знак модуля 1) построить график функции, опустив знак модуля 2) отобразить симметрично оси Ох часть графика, расположенного в области отрицательных значений у.

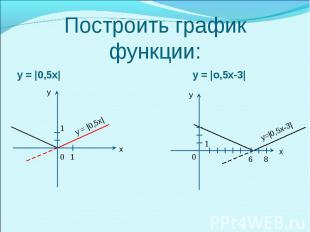
у = |0,5х| у = |0,5х|

1) найти корни выражений, стоящих под знаком модуля; 1) найти корни выражений, стоящих под знаком модуля; 2) на числовой прямой проставить эти корни; 3) в каждом промежутке определить вид функции; 4) построить график в каждом промежутке.

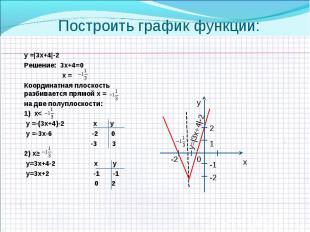
у =|3х+4|-2 у =|3х+4|-2 Решение: 3х+4=0 х = Координатная плоскость разбивается прямой х = на две полуплоскости: 1) х< у =-(3х+4)-2 х у у =-3х-6 -2 0 -3 3 2) х≥ у=3х+4-2 х у у=3х+2 -1 -1 0 2

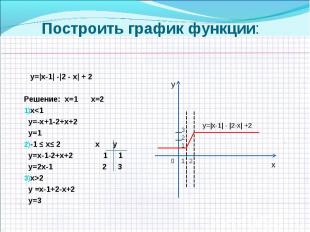
у=|х-1| -|2 - х| + 2 у=|х-1| -|2 - х| + 2 Решение: х=1 х=2 х<1 у=-х+1-2+х+2 у=1 -1 ≤ х≤ 2 х у у=х-1-2+х+2 1 1 у=2х-1 2 3 х>2 у =х-1+2-х+2 у=3

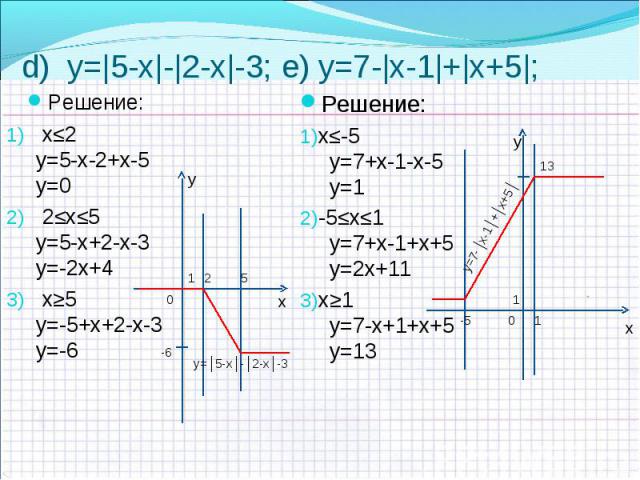
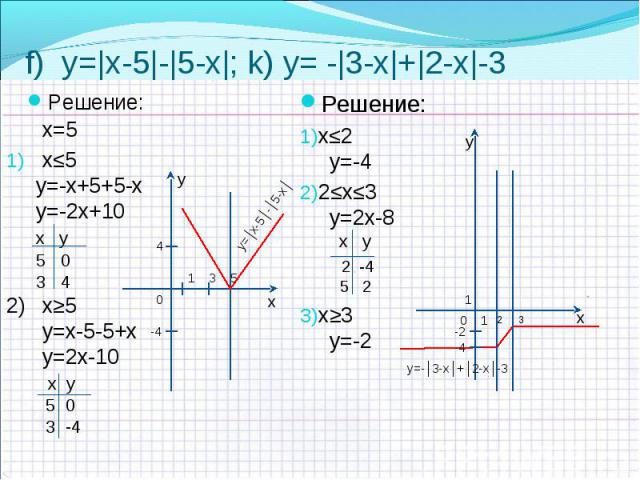
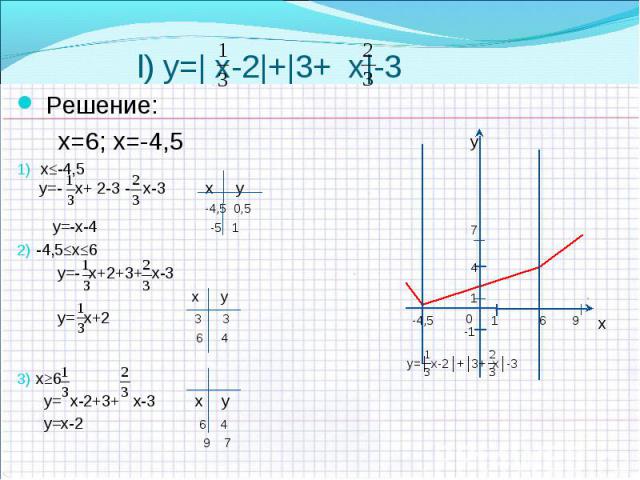
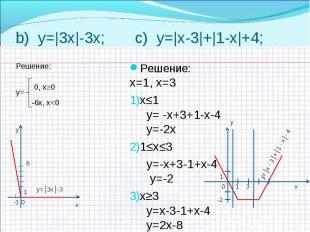
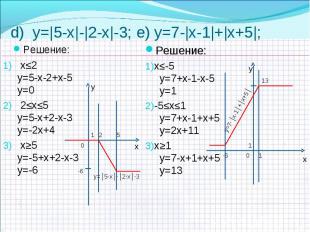
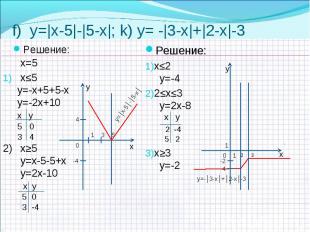
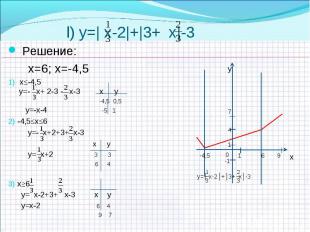
a) y=|х-1|+|х-2|+х слайд №9 a) y=|х-1|+|х-2|+х слайд №9 b) y=|3х|-3х слайд №10 c) y=|х-3|+|1-х|+4 слайд №10 d) y=|5-х|-|2-х|-3 слайд №11 e) y=7 -|х-1|+|х+5| слайд №11 f) y=|х-5|+|5-х| слайд №12 k) y=-|3-х|+|2-х|-3 слайд №12 l) y=| х-2|+|3+ х|-3 слайд №13

Решение: Решение: х=1; х=2 х< 1 у=-х+1-2+х+2 у=1 1≤х≤ 2 у=х-1-2+х+2 у=2х -1 х>2 у=х-1+2-х+2 у=3

Решите уравнение: │х-3│+│1-х│=4 (х=3; х=1) Решите уравнение: │х-3│+│1-х│=4 (х=3; х=1) Постройте график функции: y= │х-3│+│1-х│- 4 Имея корни решенного уравнения и рассматривая график построенной функции, делаем вывод: корни данного уравнения – это координаты точки пересечения графика с осями координат. Таким образом строим графики функций, содержащие выражения под знаком модуля опираясь на решение уравнения, содержащего выражения под знаком модуля.