Презентация на тему: Правильные многогранники

Компьютерная поддержка темы"Правильные многогранники"Автор:Сердюкова Настя Руководитель:Лебедева

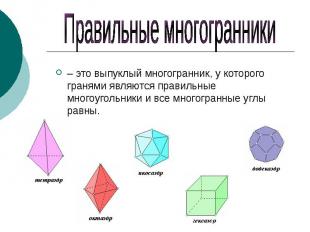
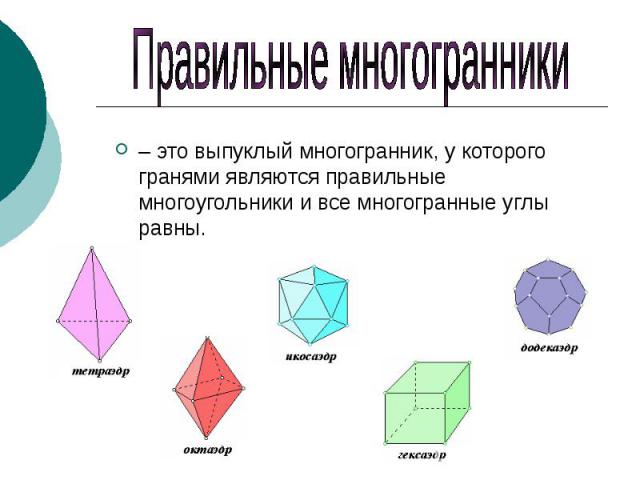
Правильные многогранники – это выпуклый многогранник, у которого гранями являются правильные многоугольники и все многогранные углы равны.

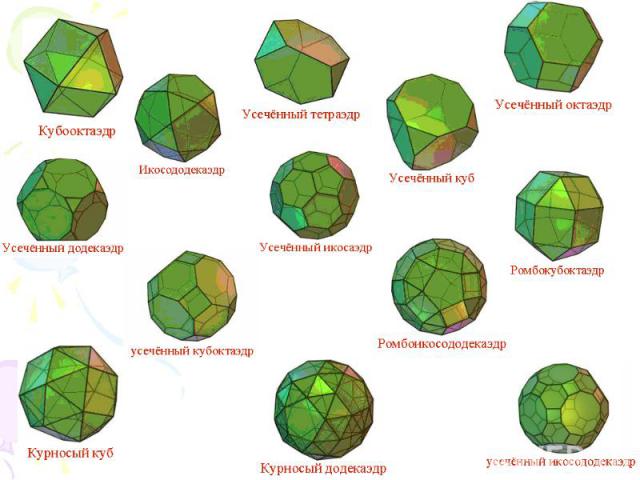
Полуправильные многогранники – это выпуклый многогранник, гранями которого является правильные многоугольники (возможно, с разным числом сторон) и все многогранные углы раны. К полуправильным многогранникам относятся правильные n-угольные призмы, все ребра которых равны, а также так называемые антипризмы. Кроме этих двух бесконечных серий полуправильных многогранников имеется еще 13 полуправильных многогранников, которые впервые открыл и описал Архимед, - это тела Архимеда

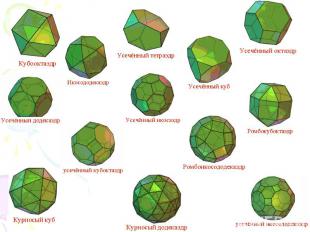
Теорема Эйлера Попытка классификации многогранников привела в 1750 году известнейшего математика Леонарда Эйлера к следующему результату. В - Р + Г = 2 Где В – число вершин, Р – число ребер, Г – число граней многогранника.Проверим теорему Эйлера на полуправильных многогранниках. В – Р + Г = 2 Кубооктаэдр: 12 – 24 + 14 = 2 ПОДХОДИТИкосододекаэдр: 30 – 60 + 32 = 2 ПОДХОДИТКурносый додекаэдр: 60-150+92=2 ПОДХОДИТВывод: Теорема Эйлера выполняется и для полуправильных многогранников.

Звездчатые многогранники — это правильный невыпуклый многогранник. Они получаются из правильных многогранников продолжением их граней или рёбер.

Применение компьютерной программы"Математика" При помощи компьютерной программы мы можем изображать правильные многогранники и получать из них полуправильные. Для этого нужно набрать<<Graphics `Polyhedra` p = Polyhedron [Dodecahedron]Show [p, Boxed->False] и мы получим додекаэдр. Если вместо Dodecahedron написать соответственно Tetrahedron, Octahedron, Hexahedron, Icosahedron, то получим изображения тетраэдра, октаэдра, куба и икосаэдра.В программе «Математика» имеется операция «Truncate», при которой от правильных многогранников отсекаются углы и в результате получаются полуправильные многогранники. Так, например, использование команды <<Graphics `Polyhedra`p = Polyhedron [Dodecahedron]Show [Truncate[p], Boxed->False] Приводит к усеченному додекаэдру.

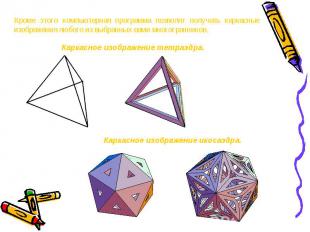
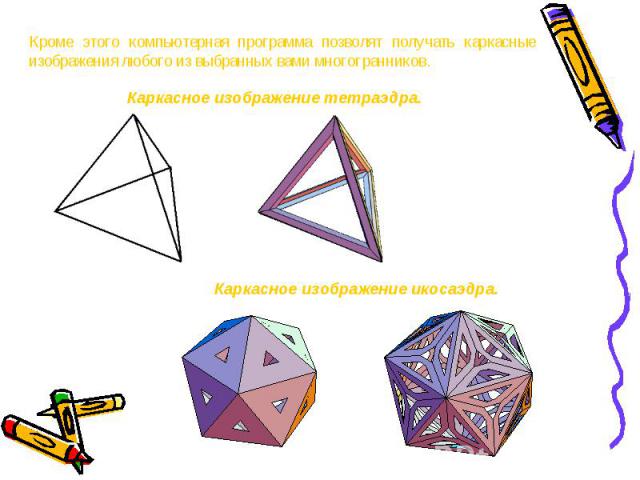
Кроме этого компьютерная программа позволят получать каркасные изображения любого из выбранных вами многогранников. Каркасное изображение тетраэдра.Каркасное изображение икосаэдра.

Решим задачу по получению звезды Кеплера. Этот звездчатый многогранник не является правильным. Он был открыт Кеплером и назван «Stella octangula» (Звезда восьмиугольная).1.Наберем команду:<<Graphics `Polyhedra`p = Polyhedron [Tetrahedron,]Show [p, Boxed->False] Получим изображение тетраэдра.2.Произведем операцию усечения тетраэдра с коэффициентом 0,5 и получим октаэдр:<<Graphics `Polyhedra`p = Polyhedron [Tetrahedron,]Show [Stellate[p,0,5],Boxed->False] 3.Операция двойного усечения:<<Graphics `Polyhedra`p = Polyhedron [Tetrahedron,]Show[Stellate[Stellate[p,0,5]0,5],Boxed->False] Приводит к получению звезды Кеплера.

Заключение Познакомившись с компьютерной программой «Математика» я увидела большие возможности этой программы. Поставленную перед собой цель я выполнила. Моя работа является электронным, наглядным пособием для изучения темы «Правильные и полуправильные многогранники». Кроме того я считаю, что использование программы «Математика» возможно и необходимо на уроках математики при изучении различных тем.