Презентация на тему: Правильные многогранники 10 класс

Международная научно-практическая конференция «От школьного проекта – к профессиональной карьере» Тема учебного проекта: «Правильные многогранники»Творческое название: «Ключи мироздания»Мы мирозданье многогранником зовём, И тщимся сосчитать бесчисленные грани, Мы острые углы отыскиваем в нём -  И удивляемся бесплодности исканий… Руководитель проекта: Долгова Зинаида Александровна, преподаватель математики.

Содержание: Введение; Геометрическая справка (правильные многогранники) – 10, 11, 12, 13, 19, 20, 21, 22, 24 слайды;Золотое сечение (пропорция) и его роль в конструкции Платоновых тел – 18, 26 слайды;Тайны планет и Вселенной (гипотезы и взгляды) – 27, 28, 29, 30, 31 слайды;Многогранники вокруг нас – 23, 25, 32 слайды;Египетские пирамиды – 14, 15, 16, 17 слайды;Заключение (вывод).

Введение«Живые источники математического творчества неотделимы от интереса познания природы». Таковыми источниками мы можем назвать многогранники. В данном проекте подробно исследуем три вида этих замечательных геометрических тел – тетраэдр, икосаэдр и додекаэдр.

Актуальность исследования Актуальность данного исследования состоит в том, что правильные многогранники – «вечные» тела. Интерес к ним тонкой нитью проходит через спираль всех времен. Чем же обусловлен столь бессмертный интерес? Считается, что в основе строения Платоновых тел заложены пропорции всего, из чего состоит мир. Поэтому эти уникальные фигуры и получили название «ключей мироздания».

Основополагающий вопрос: в чём состоит уникальность правильных многогранников как пространственных тел?Гипотеза: правильные многогранники не только занимательные геометрические фигуры, но и часть жизни человека.

Объект исследования: правильные многогранники – тетраэдр, гексаэдр, октаэдр, икосаэдр, додекаэдр.Предмет исследования: аналоги правильных многогранников в нашей жизни.Цель работы: показать связь математики и жизни, используя электронные средства; сделать сухие факты, изложенные математическим языком более яркими и интересными; понять, что законы математики взяты из природы и объясняют природу.

Задачи проекта: 1. Изучение особенностей строения правильных многогранников;2. Исследование аналогов многогранников в природе;3. Анализ полученных исследований;4. Понятие о роли Золотой пропорции в правильных многогранниках;5. Выявление связи геометрии и природы.

Методы исследования:Эмпирические: сравнение, математические расчёты;Теоретические: анализ полученных данных, восхождение от абстрактного к конкретному;Общие методы: применение аналога трёхмерного изображения.

Великие люди, изучавшие правильные многогранникиТеория многогранников, в частности выпуклых многогранников,— одна из самых увлекательных глав геометрии. Л. А. Люстерник Древнегреческий учёный, философ - идеалист ПлатонВеликий математик, философ ЕвклидВеликий математик, инженер древности Архимед

Геометрическая справкаЕвклид вовсе не собирался выпускать систематический учебник геометрии.Он задался целью написать сочинение о правильных многогранниках, рассчитанное на начинающих, в силу этого ему пришлось изложить все необходимые сведенияд’ Арси ТомпсонМногогранник - геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней называются ребрами многогранника, а концы ребер — вершинами многогранника. Многогранник называется правильным, если все его грани — правильные одинаковые многоугольники и все многогранные углы при вершинах равны. Существует 5 видов правильных многогранников: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

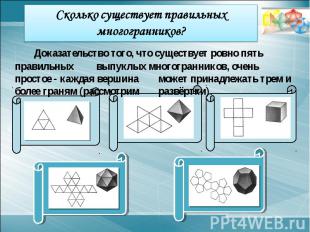
Сколько существует правильных многогранников?Доказательство того, что существует ровно пять правильных выпуклых многогранников, очень простое - каждая вершина может принадлежать трем и более граням (рассмотрим развёртки).

Замечательные свойства многогранниковЕсли центры граней правильного многогранника принять за вершины нового многогранника, то получится правильный многогранник, дуальный (двойственный) исходному. Октаэдру двойственен куб. Несложно догадаться, что тетраэдр дуален сам себе. Так что, в одном из смыслов, получаем три типа правильных многогранников. Понятно, правда, что никакого философского смысла в этом нет, а только геометрический.На гравюре "Четыре тела" Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.

ТетраэдрТетраэдр (от греческого tetra – четыре и hedra – грань) - правильный выпуклый многогранник, составленный из 4-ёх равносторонних треугольников. Тетраэдр имеет 4 вершины и 6 ребёр. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.Тетраэдр символизирует огонь устремлённой вверх вершиной

Египетские пирамиды – аналоги тетраэдра«Всё боится времени, только время боится пирамид»

Теория МореАббат Море, директор Буржской обсерватории во Франции, утверждал, что, если сложить четыре основания пирамиды Хуфу, то мы получим периметр, который нужно разделить на 2 высоты пирамиды. Тем самым (по утверждению Море) мы получим число π.Давайте попробуем сами доказать эту теорию!

Собственное доказательство теории Море1) Сложим четыре основания пирамиды:230,38 • 4 = 921,52 м – периметр.2) Разделим полученный периметр на удвоенное произведение высоты пирамиды:921,52 : (2 • 146,6) = 3,1429 – приближённое значение числа π.

Но на этом секреты Великой пирамиды не заканчиваются…Обмеры пирамид показывают, что все величины пирамиды соответствуют «золотому сечению». Стены пирамиды поднимаются под углом 52 градуса. Этот угол воплощает в пирамиде математическое значение числа "пи", но что еще более важно, только при угле в 52 градуса отношение высоты пирамиды к периметру ее основания в точности равно отношению диаметра окружности к ее длине. Геометрические параметры пирамиды с углом 52 градуса отвечают условиям "золотого сечения".

Золотая пропорция"Невозможно, чтобы две вещи совершенным образом соединились без третьей, так как между ними должна появиться вещь, которая скрепляла бы их. Это наилучшим образом может выполнить пропорция, ибо если три числа обладают тем свойством, что среднее так относится к меньшему, как большее к среднему, и, наоборот, меньшее так относится к среднему, как среднее к большему, то последнее и первое будет средним, а среднее - первым и последним. Таким образом, все необходимое будет тем же самым, а так как оно будет тем же самым, то оно составит целое".Пифагореец Тимей«Золотая» пропорция — это такое деление целого на две неравные части, при котором большая часть так относится к меньшей, как целое относится к большей:b / a = (a + b) / b     

ОктаэдрОктаэдр (от греческого okto – восемь и hedra – грань) -правильный выпуклый многогранник, составленный из 8 равносторонних треугольников. Каждая из 6 вершин октаэдра является вершиной 4 равносторонних треугольников, поэтому сумма углов при вершине равна 240 °.У октаэдра 12 ребер.

Гексаэдр (куб)Гексаэдр (куб) (от греческого hex — шесть и hedra — грань) - правильный многогранник, составленный из 6 квадратов. Каждая из 8 вершин куба является вершиной 3 квадратов, поэтому сумма углов при вершине равна 180 °.У гексаэдра 12 ребер.

ИкосаэдрИкосаэдр (от греческого ico – двадцать и hedra – грань). Правильный выпуклый многогранник, составленный из 20 правильных треугольников. Каждая из 12 вершин икосаэдра является вершиной 5 равносторонних треугольников, поэтому сумма углов при вершине равна 300°.У икосаэдра 30 ребер. Как и у всех правильных многогранников ребра икосаэдра имеют равную длину, а грани - равную площадь.

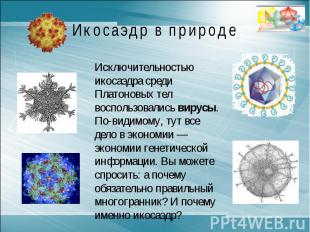
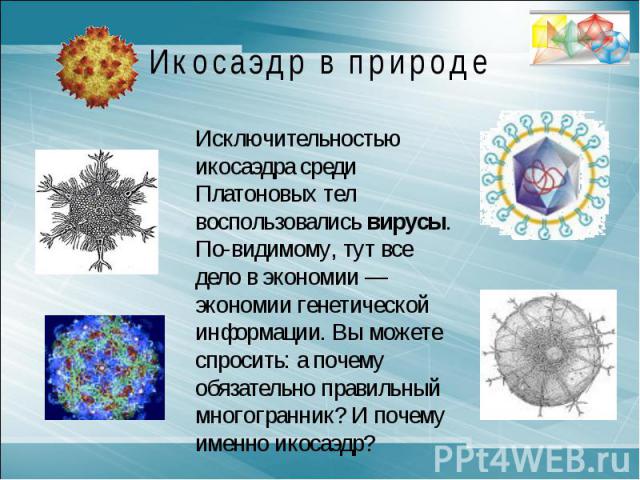
Икосаэдр в природеИсключительностью икосаэдра среди Платоновых тел воспользовались вирусы. По-видимому, тут все дело в экономии — экономии генетической информации. Вы можете спросить: а почему обязательно правильный многогранник? И почему именно икосаэдр?

ДодекаэдрДодекаэдр (от греческого dodeka – двенадцать и hedra – грань) - правильный многогранник, составленный из 12 равносторонних пятиугольников. Додекаэдр имеет 20 вершин и 30 ребер. Вершина додекаэдра является вершиной 3 пятиугольников, таким образом, сумма плоских углов при каждой вершине равна 324°.

Додекаэдр в природе (фуллерен)Удивительные свойства медицинских препаратов, основанных на фуллеренах, определяются свойствами «золотого сечения». Ведь Архимедов усеченный икосаэдр является геометрической структурой, буквально «нашпигованной» золотыми пропорциями!

КристаллыКристаллы — тела, имеющие многогранную форму. Вот один из примеров таких тел: кристалл пирита (сернистый колчедан FeS) — природная модель додекаэдра. Пирит (от греч. “пир” — огонь) — сернистое железо или серный колчедан, наиболее распространенный минерал из группы сульфидов. Размеры кристаллов пирита часто достигают нескольких сантиметров и являются хорошим коллекционным материалом. От других подобных ему минералов отличается твердостью: царапает стекло.

Золотая пропорция в додекаэдре и икосаэдреДодекаэдр и двойственный ему икосаэдр занимают особое место среди Платоновых тел. Прежде всего, необходимо подчеркнуть, что геометрия додекаэдра и икосаэдра непосредственно связана с золотой пропорцией.

Устройство мироздания по ПлатонуЧетыре многогранника олицетворяли четыре сущности или «стихии». Тетраэдр символизировал огонь, так как его вершина устремлена вверх. Куб – землю, как самый «устойчивый». Икосаэдр – воду, так как он самый «обтекаемый». Октаэдр – воздух, как самый «воздушный». Пятый многогранник «додекаэдр» воплощал в себе «всё сущее»; символизировал всё мироздание, считался главным.

Космологическая гипотеза КеплераКеплер Иоганн (1571-1630г) – немецкий астроном. Открыл законы движения планет. В 1596 году Кеплер предложил правило, по которому вокруг сферы Земли описывается додекаэдр, а в нее вписывается икосаэдр («Гармония мира», 1619г.) И.Кеплер предположил, что расстояния между орбитами планет можно получить на основании Платоновых тел, вложенных друг в друга. Результаты его расчётов хорошо согласовались с действительными расстояниями между планетными орбитами.

Тайны планет и Вселенной Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.

Додекаэдро-икосаэдрическая доктрина «Земля, если взглянуть на нее сверху, похожа на мяч, сшитый из 12 кусков кожи».Сократ

Додекаэдро-икосаэдрическая доктринаДодекаэдрическая структура, по мнению Д. Винтера (американского математика), присуща не только энергетическому каркасу Земли, но и строению живого вещества. Структура ДНК генетического кода жизни – представляет собой четырехмерную развертку (по оси времени) вращающегося додекаэдра!

Многогранники в искусствеМатематик, так же как и художник или поэт, создает узоры, и еслиего узоры более устойчивы, то лишь потому, что они составлены из идей.Гравюра «Звёзды» М. ЭшераРаботы Ф. Джовани да Верона

ЗаключениеВысшее назначение математики- находить порядок в хаосе, который нас окружаетНорберт Винер

Список использованной литературыА. Деко «Великие загадки истории», Москва «Вече», 2006 г.«Я познаю мир. Загадки истории», Москва «АСТ» 2002 г.Интернет-ресурсыhttp://dxdt.ru занимательный интернет-журнал.htm;Египетские Пирамиды_ Пирамида Хеопса.htm;Академия Тринитаризма -- Институт Золотого Сечения - Математика Гармонии.htm;Правильные многогранники.html;http://polyhedron.boom.ru/pages/tetra.htm ;http://www.inauka.ru/analysis/article85470.html.

Спасибо за внимание!