Презентация на тему: Использование графовых моделей при решении задач

Использование графовых моделей при решении задач УЧИТЕЛЬ МОУ СОШ № 2 НАУМЕНКО Н. Г.

ГРАФИЧЕСКАЯ МОДЕЛЬ – ОДНА ИЗ НАИБОЛЕЕ УДАЧНЫХОПОР ДЛЯ ПОСТРОЕНИЯ МЫСЛИТЕЛЬНОЙ МОДЕЛИ ЗАДАЧИ :ПРИ ПРАВИЛЬНОМ ПОСТРОЕНИИ ОНА ДОСТАТОЧНО КОНКРЕ-ТНА, ЛЕГКО ВОСПРИНИМАЕТСЯ ЗРИТЕЛЬНО, ПОЛНОСТЬЮ ОТРАЖАЕТ ВНУТРЕННИЕ СВЯЗИ И КОЛИЧЕСТВЕННЫЕ ОТНОШЕНИЯ. ГРАФЫ СПОСОБСТВУЮТ РАЗВИТИЮ ЛОГИЧЕСКОГО И АБСТРАКТНОГО МЫШЛЕНИЯ.

ТРИ ЭТАПА В ОБУЧЕНИИ МЛАДШИХ ШКОЛЬНИКОВ В РЕШЕНИИ ЗАДАЧ С ПОМОЩЬЮ ГРАФОВ. ПОДГОТОВИТЕЛЬНЫЙ ЭТАП:-ВВЕДЕНИЕ УСЛОВНОГО ОБОЗНАЧЕНИЯ ОБЪЕКТОВ И СВЯЗЕЙ МЕЖДУ НИМИ;ПОСТРОЕНИЕ ГРАФИЧЕСКОЙ МОДЕЛИ, ОТРАЖАЮЩЕЙ ВСЕ ДАННЫЕ ЗАДАЧИ. ПЕРВЫЙ ЭТАП:РЕШЕНИЕ ЗАДАЧ С НЕБОЛЬШИМ КОЛИЧЕСТВОМ ОБЪЕКТОВ И СВЯЗЕЙ МЕЖДУ НИМИ. ВТОРОЙ ЭТАП:РЕШЕНИЕ ЗАДАЧ С УВЕЛИЧЕНИЕМ КОЛИЧЕСТВА ОБЪЕКТОВ И УВЕЛИЧЕНИЕ КО-ЛИЧЕСТВА СВЯЗЕЙ МЕЖДУ ОБЪЕКТАМИ; ИСПОЛЬЗОВАНИЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ БОЛЕЕ ОДНОГО ВИДА ГРАФОВ.

ТРИ ГРУППЫ ЗАДАЧ ПЕРВОГО ЭТАПА:ЗАДАЧИ, ДЛЯ РЕШЕНИЯ КОТОРЫХ УДОБНЕЕ ИСПОЛЬЗОВАТЬ ОРИЕНТИРОВАННЫЕ ГРАФЫ ( В ТОМ ЧИСЛЕ ГРАФЫ С РЁБРАМИ ДВУХ ЦВЕТОВ);ЗАДАЧИ, ДЛЯ РЕШЕНИЯ КОТОРЫХ УДОБНЕЕ ИСПОЛЬЗОВАТЬ ОРИЕН- ТИРОВАННЫЕ ГРАФЫ;ЗАДАЧИ, ДЛЯ РЕШЕНИЯ КОТОРЫХ УДОБНЕЕ ИСПОЛЬЗОВАТЬ ДВУ- ДОЛЬНЫЕ ГРАФЫ С РЁБРАМИ ДВУХ ЦВЕТОВ.

К КОНЦУ ПЕРВОГО ЭТАПА УЧАЩИЕСЯ ДОЛЖНЫ УМЕТЬ:ПОЛНО И ПРАВИЛЬНО РЕШАТЬ ЗАДАЧИ ИЗУЧЕННЫХ ВИДОВ, САМОСТОЯТЕЛЬНО ВЫБИРАЯ, С ПОМОЩЬЮ КАКОГО ВИДА ГРАФА ЕЁ РЕШАТЬ;- СОСТАВЛЯТЬ ГРАФОВЫЕ МОДЕЛИ РАЗЛИЧНЫХ ВИДОВ, ПРАВИЛЬНО ИХ ЧИТАТЬ.

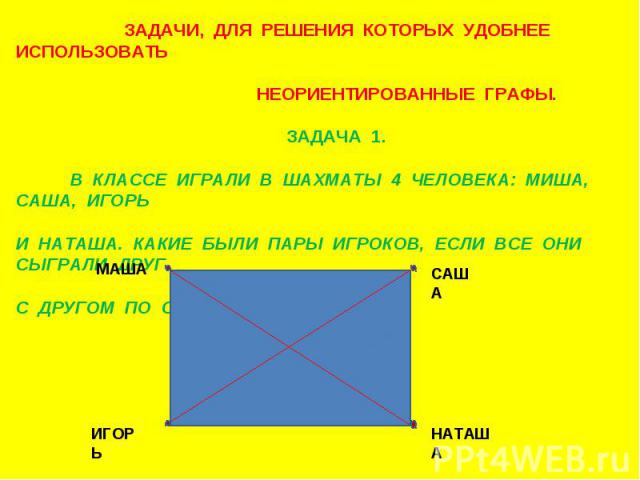
ЗАДАЧИ, ДЛЯ РЕШЕНИЯ КОТОРЫХ УДОБНЕЕ ИСПОЛЬЗОВАТЬ НЕОРИЕНТИРОВАННЫЕ ГРАФЫ. ЗАДАЧА 1. В КЛАССЕ ИГРАЛИ В ШАХМАТЫ 4 ЧЕЛОВЕКА: МИША, САША, ИГОРЬ И НАТАША. КАКИЕ БЫЛИ ПАРЫ ИГРОКОВ, ЕСЛИ ВСЕ ОНИ СЫГРАЛИ ДРУГС ДРУГОМ ПО ОДНОМУ РАЗУ?

ГРАФ ( ОТ ГРЕЧ. ПИШУ, ЧЕРЧУ, РИСУЮ)..ТОЧКИ, КОТОРЫМИ ОБОЗНАЧАЛИ ИГРОКОВ, НАЗЫВАЮТСЯ ВЕРШИНАМИ ГРАФА, А ОТРЕЗКИ( ДУГИ, СТРЕЛКИ), ИХ СОЕДИНЯЮЩИЕ, - РЁБРАМИ ГРАФА.

ЗАДАЧА 2. ПЯТЬ ЧЕЛОВЕК ОБМЕНЯЛИСЬ РУКОПОЖАТИЯМИ. СКОЛЬКО БЫЛО РУКОПОЖАТИЙ?

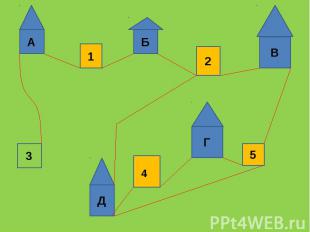
ЗАДАЧАЖИТЕЛИ 5 ДОМОВ ПОССОРИЛИСЬ ДРУГ С ДРУГОМ И, ЧТОБЫ НЕ ВСТРЕЧАТЬСЯ У КОЛОДЦЕВ, РЕШИ-ЛИ ПОДЕЛИТЬ КОЛОДЦЫ ТАК, ЧТОБЫ КАЖДЫЙХОДИЛ К «СВОЕМУ» КОЛОДЦУ ПО «СВОЕЙ» ДОРОЖКЕ. УДАСТСЯ ЛИ ИМ ЭТО СДЕЛАТЬ?

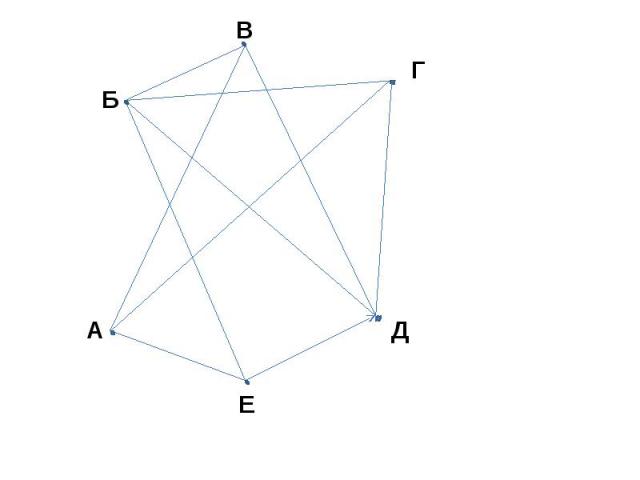
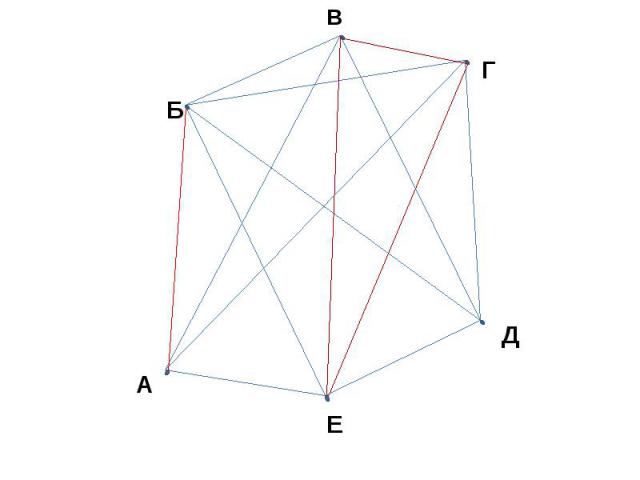
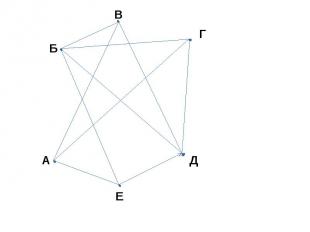
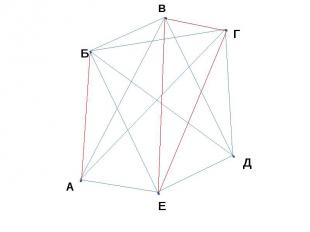
ЗАДАЧА В ШКОЛЬНОЧ ЧЕМПИОНАТЕ ПО ФУТБОЛУ УЧАСТВУЮТ 6 КОМАНД, А, Б, В, Г, Д, Е. КАЖДЫЕ ДВЕ КОМАНДЫ ДОЛЖНЫ ВСТРЕТИТЬСЯ ДРЕГ С ДРУГОМ ОДИН РАЗ. ЧЕРЕЗ СКОЛЬКО ДНЕЙ ПОСЛЕ НАЧАЛА СОРЕВНОВАНИЯ СТАЛО ИЗВЕСТНО, ЧТО КОМАНДА А УЖЕ СЫГРАЛА С КОМАНДАМИ В, Г И Е, А КОМАНДА Д – С КОМАНДАМИ Б, В, Е И Г. КАКИЕ КОМАНДЫ ЕЩЁ НЕ СЫГРАЛИ ДРУГ С ДРУГОМ?

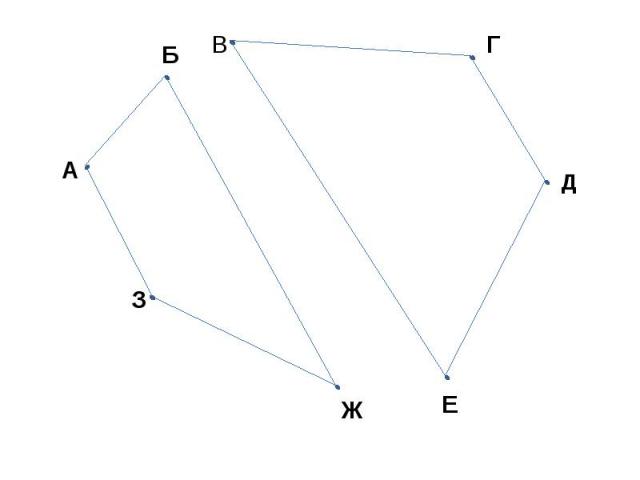
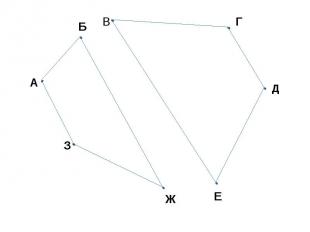
ЗАДАЧА В СТРАНЕ АЛФАВИТ 8 ГОРОДОВ: А, Б, В, Г, Д, Е, Ж, З И 8 НЕПЕРЕСЕКАЮЩИХСЯ ДОРОГ: МЕЖДУ ГОРОДАМИ А И Б, Е И Д, Б И Ж, З И А, В И Г, Г И Д, Ж И З, В И Е. МОЖНО ЛИ ПО ЭТИМ ДОРОГАМ ПРОЕХАТЬ ИЗ ГОРОДА А В ГОРОД Г?

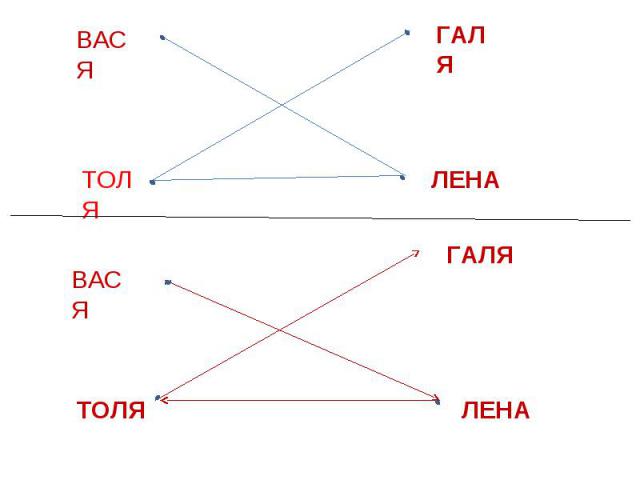
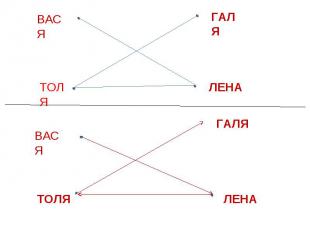
ЗАДАЧАИЗ ЛАГЕРЯ ВЫШЛИ 4 ТУРИСТА: ВАСЯ, ГАЛЯ, ТОЛЯ И ЛЕНА. ВАСЯ ИДЁТ ПОЗАДИ ЛЕНЫ, ТОЛЯ ПОЗАДИ ГАЛИ, А ЛЕНА ПОЗАДИ ТОЛИ. В КАКОМ ПОРЯДКЕ ИДУТ РЕБЯТА?

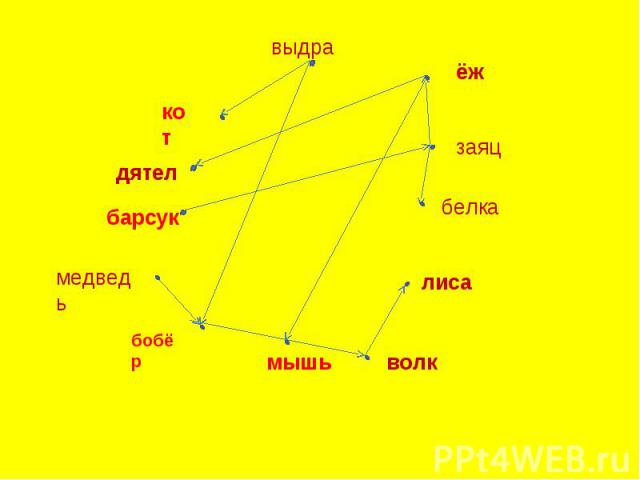
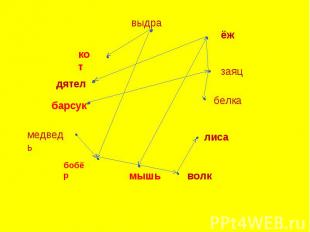
ЗАДАЧАВ ЛЕСУ КАЖДЫЙ ЗАНИМАЕТСЯ СВОИМ ДЕЛОМ: ОДНИ ПЛЕТУТ КОРЗИНЫ, ДРУГИЕ ЛОВЯТ РЫБУ. РЕМЕСЛУ МЫ НАУЧИЛИСЬ ДРУГ У ДРУГА. Кот учился у выдры, ёж – у зайца, лиса – у волка, а мышь – у ежа. Бобёр учил волка и выдру, заяц – белку, а барсук – зайца. Бобёр был учеником медведя, а ёж – учителем дятла. Лучше всех плёл корзины ёж. Чем занимались заяц, дятел, волк и лиса? Кто из зверей нашего леса раньше всех научился ловить рыбу, а кто плести корзины?

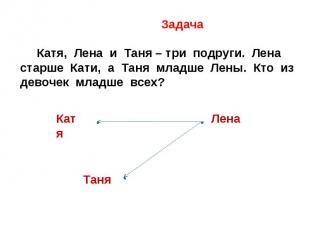
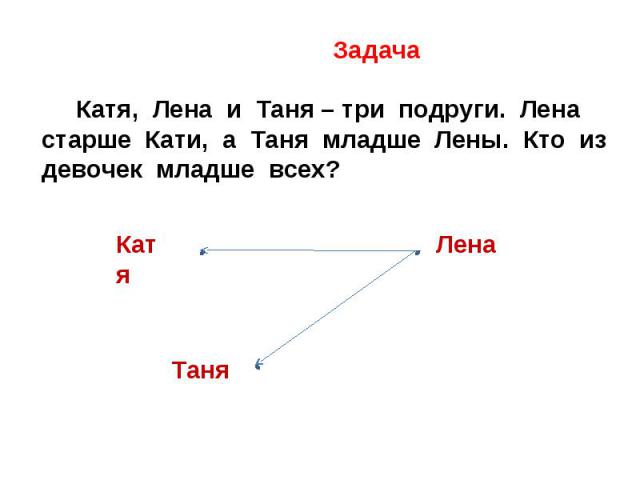
Задача Катя, Лена и Таня – три подруги. Лена старше Кати, а Таня младше Лены. Кто из девочек младше всех?

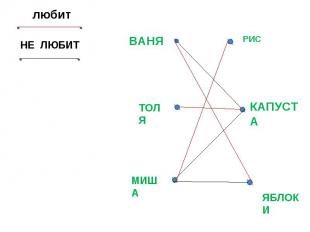
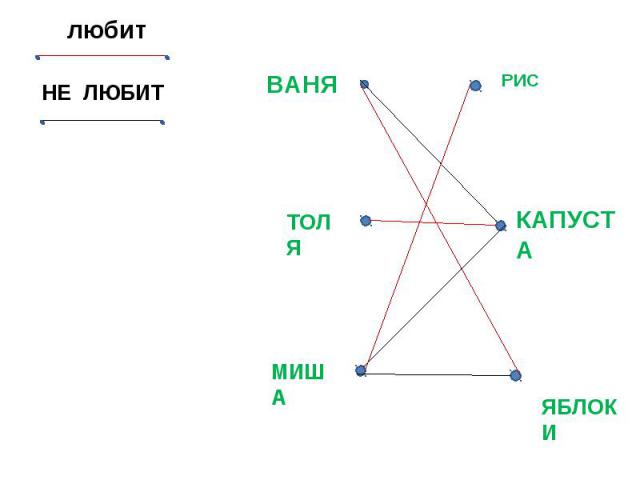
ЗАДАЧА Для Вани, Толи и Миши есть три пирога: с рисом, капустой и яблоками. Миша не любит пирог с яблоками и не ест пирог с капустой. Ваня не любит пирог с капустой. Кто что ест?