Презентация на тему: Первый признак подобия треугольников

Первый признак подобия треугольников

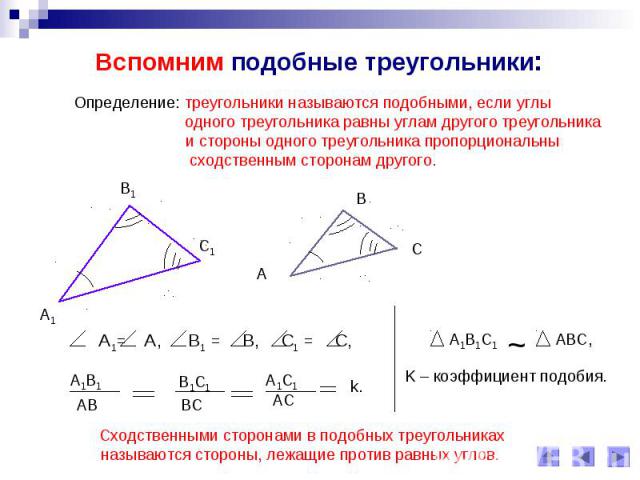
Вспомним подобные треугольники:Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональнысходственным сторонам другого. Сходственными сторонами в подобных треугольникахназываются стороны, лежащие против равных углов.

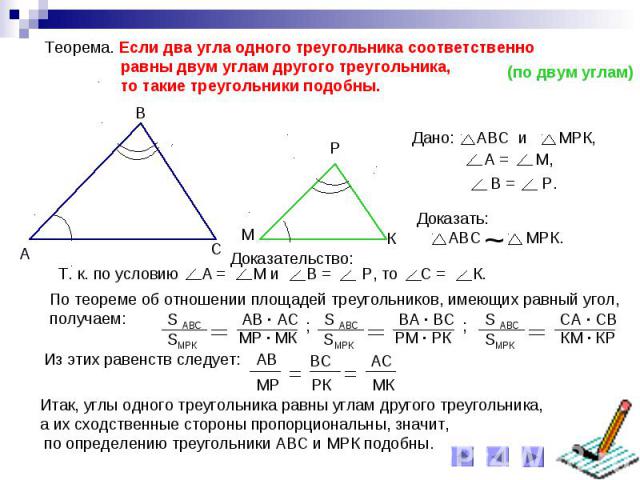
Теорема. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.По теореме об отношении площадей треугольников, имеющих равный угол,получаем:Итак, углы одного треугольника равны углам другого треугольника,а их сходственные стороны пропорциональны, значит, по определению треугольники АВС и МРК подобны.
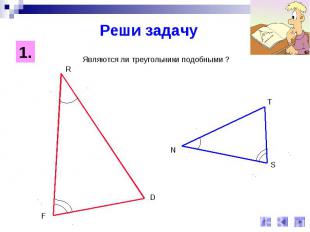
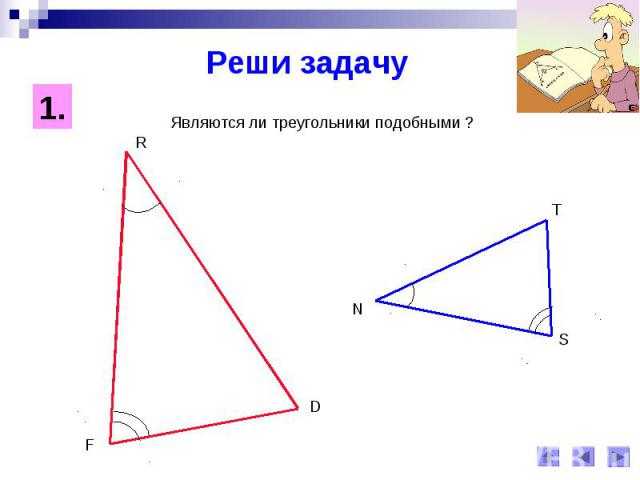
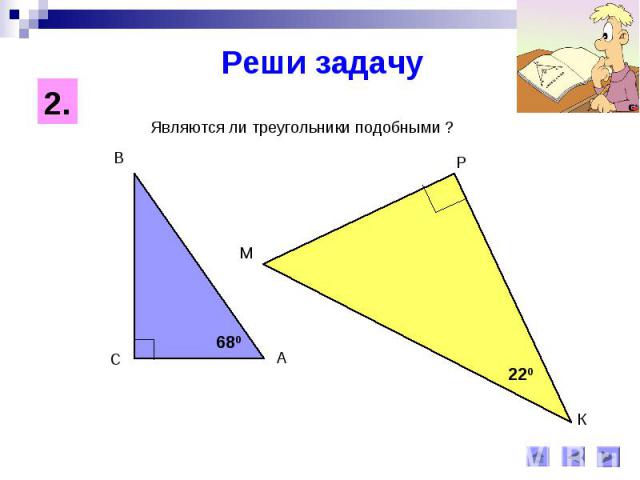
Реши задачуЯвляются ли треугольники подобными ?
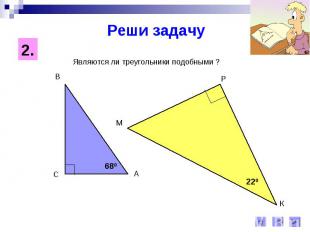
Реши задачуЯвляются ли треугольники подобными ?
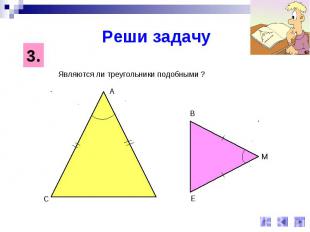
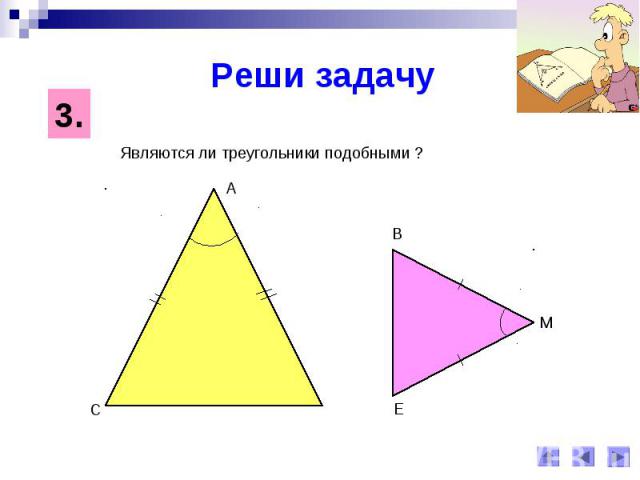
Реши задачуЯвляются ли треугольники подобными ?

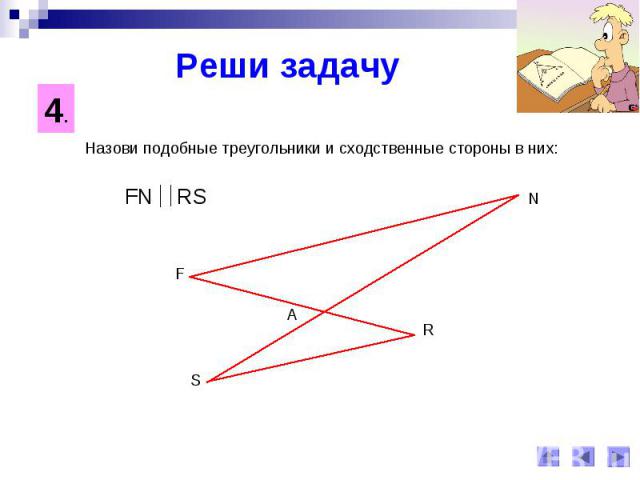
Реши задачуНазови подобные треугольники и сходственные стороны в них:

Реши задачуНазови подобные треугольники и сходственные стороны в них:
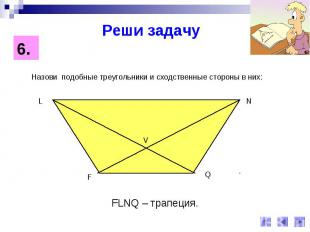
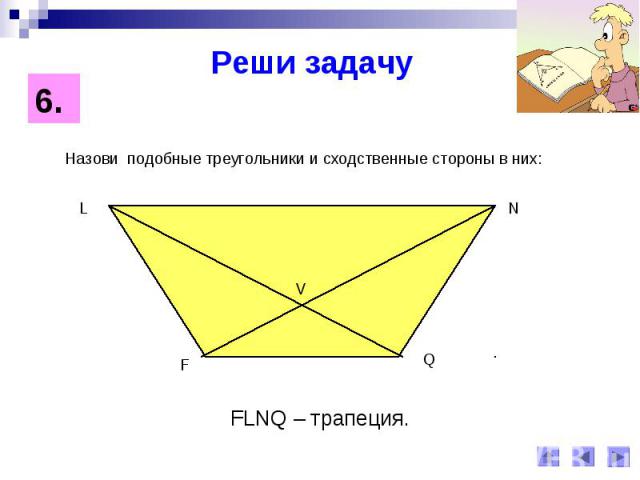
Реши задачуНазови подобные треугольники и сходственные стороны в них:
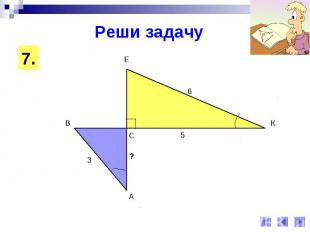
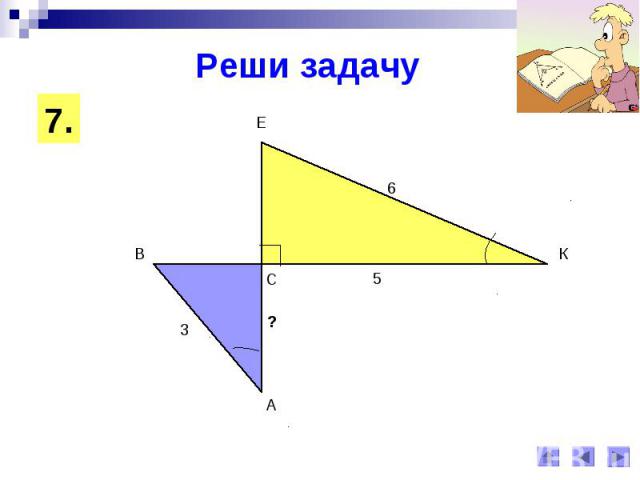
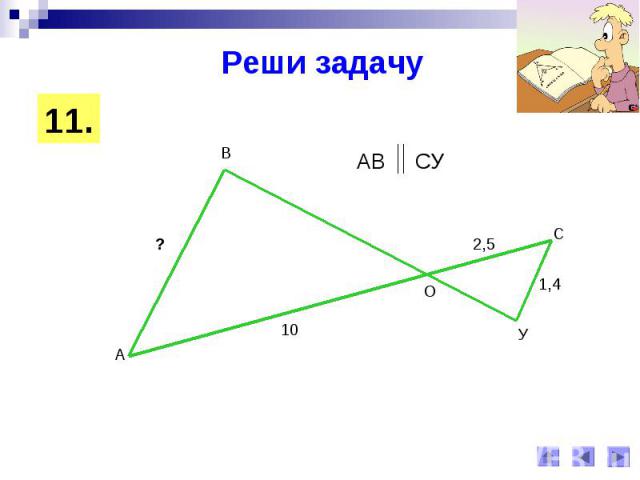
Реши задачу
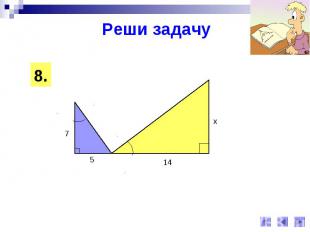
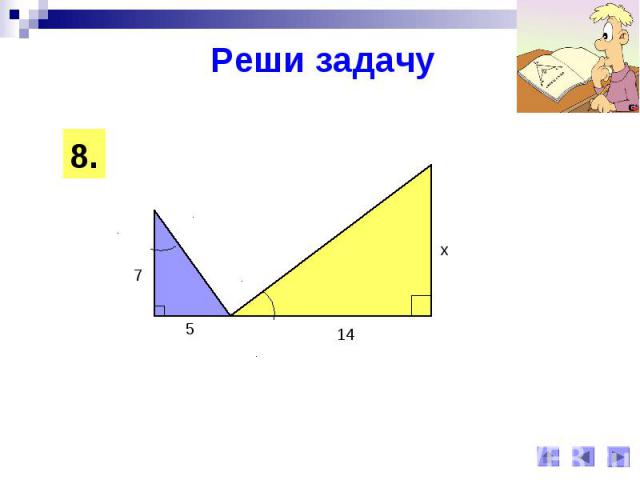
Реши задачу
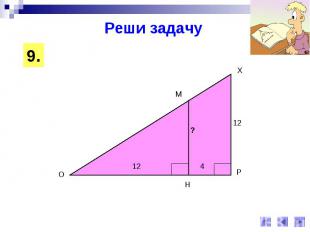
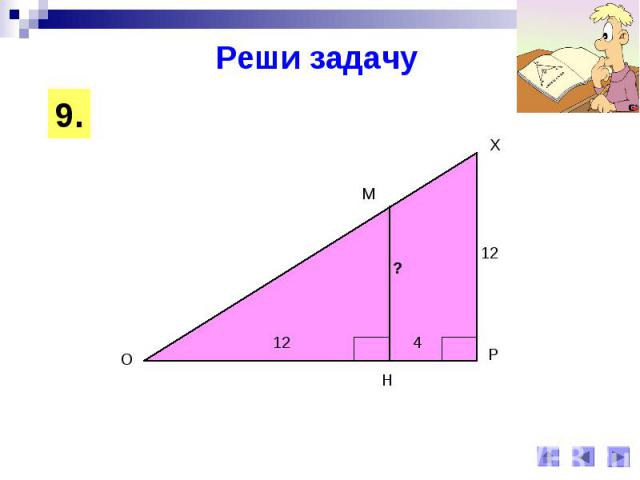
Реши задачу
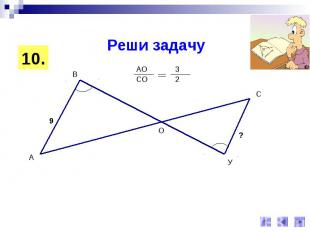
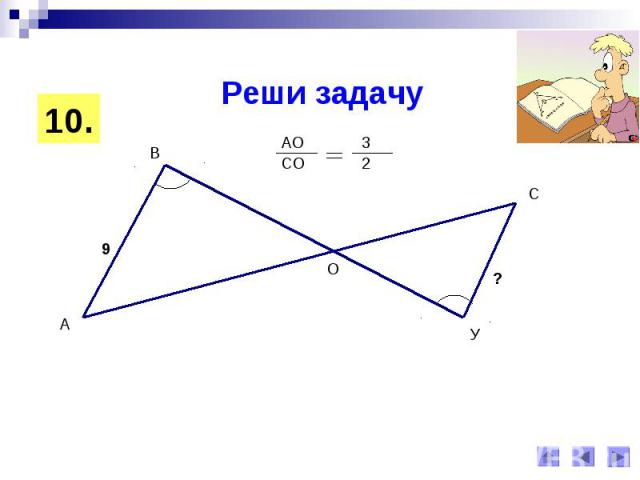
Реши задачу
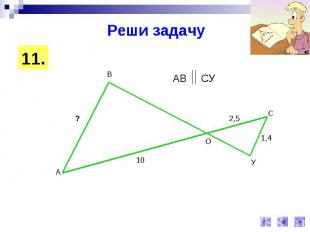
Реши задачу

Решение задачиДиагонали трапеции АВСК пересекаются в точке О. Площади треугольников ВОС и АОК относятся как 1: 9. Сумма оснований ВС и АК равна 4,8 см. Найдите основания трапеции.АВСК – трапеция, значит, ВС АК, следовательно, САК = АСВ, как накрест лежащие (секущая – АС), аналогично АКВ = СВК.Значит, по двум углам треугольники СОВ и АОК подобны, следовательно,По доказанному треугольники СОВ и АОК подобны, следовательно,ВС : АК = k, т. е. ВС : АК = 1/3, значит, ВС = 1/3 АК или АК = 3 ВС.А по условию ВС + АК = 4,8 см, значит, ВС + 3 ВС = 4,8; 4 ВС = 4,8.

Нужный выводЗначит, АОВ и САМ подобны по двум углам, следовательно,Вывод: если стороны угла пересечены параллельными прямыми, то отрезки, образованные последовательно на одной стороне угла, пропорциональны отрезкам, образованным последовательно на другой стороне угла.
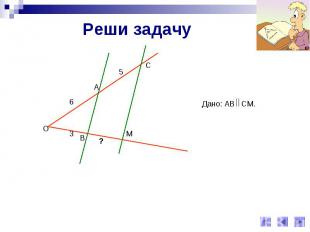
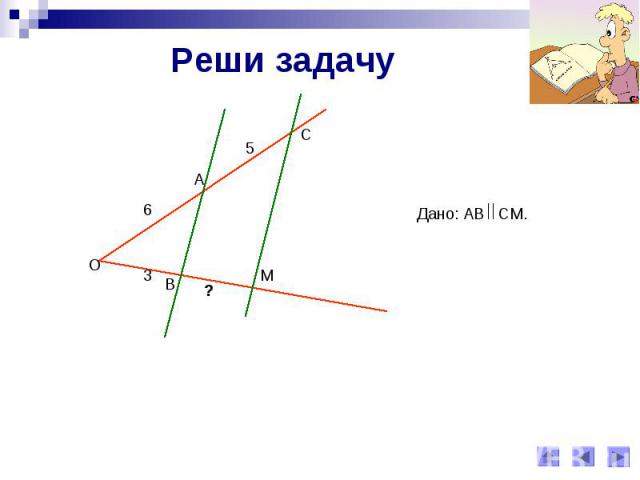
Реши задачуДано: АВ СМ.
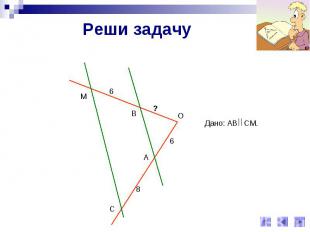
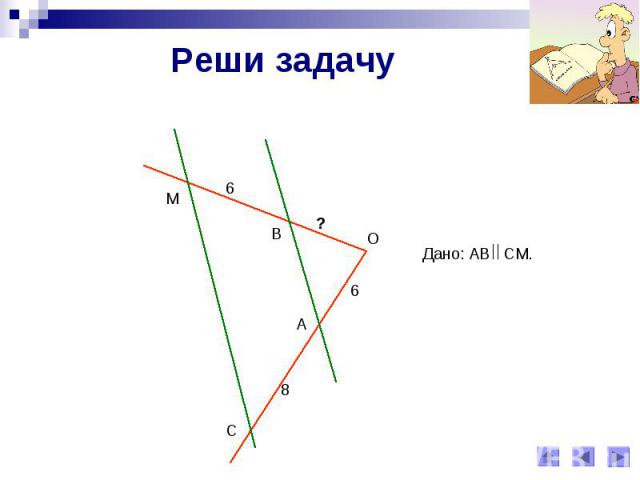
Реши задачуДано: АВ СМ.

Желаю успехов в учёбе! Михайлова Л. П.ГОУ ЦО № 173.