Презентация на тему: Второй признак подобия треугольников

Второй признак подобия треугольников

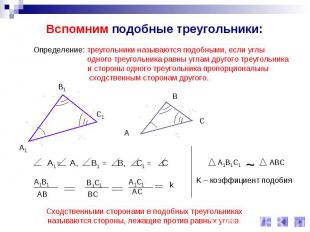
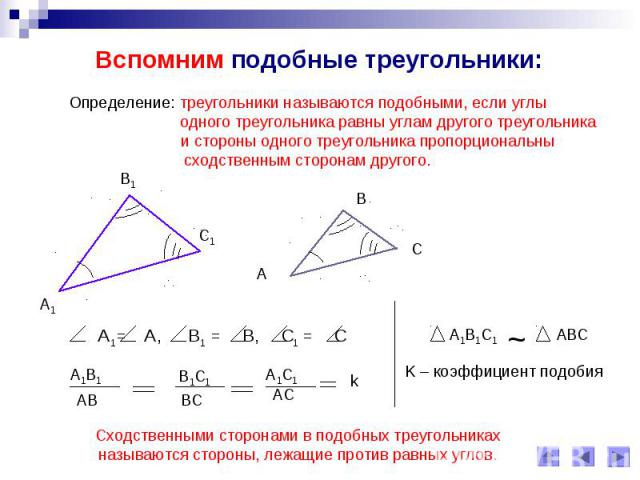
Вспомним подобные треугольники: Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональнысходственным сторонам другого.Сходственными сторонами в подобных треугольникахназываются стороны, лежащие против равных углов.

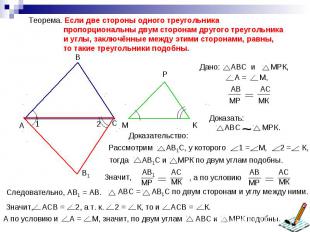
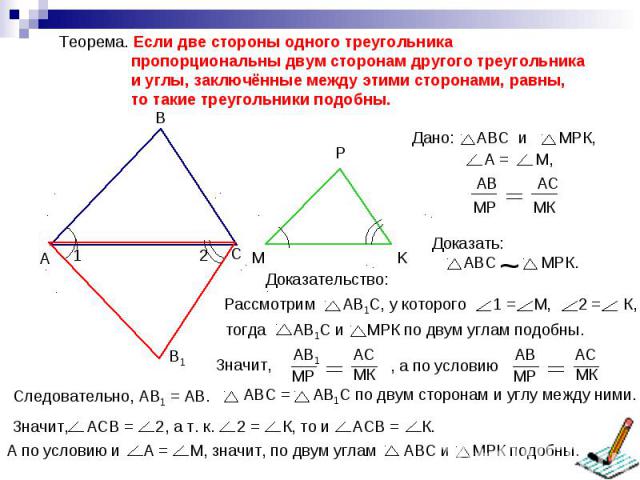
Теорема. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключённые между этими сторонами, равны, то такие треугольники подобны.

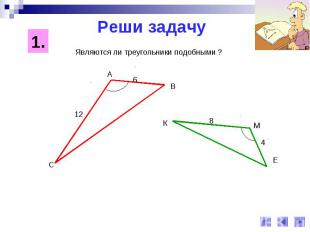
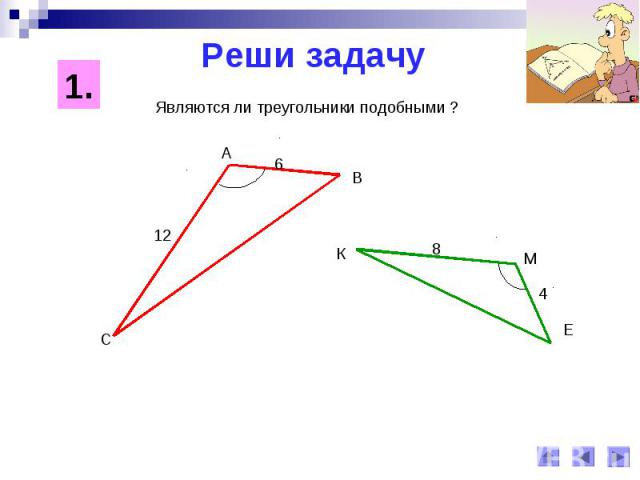
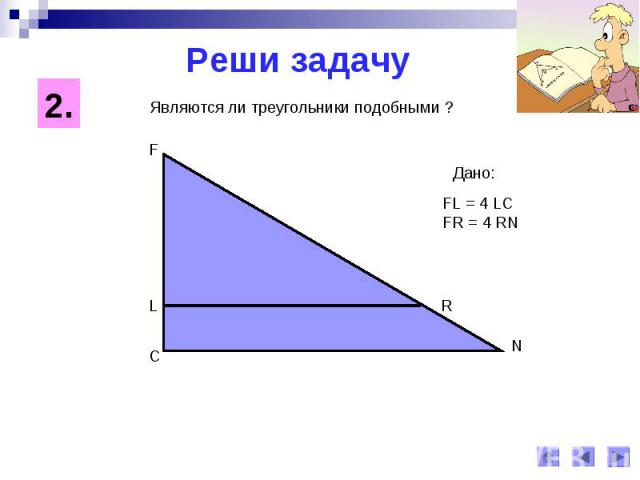
Реши задачуЯвляются ли треугольники подобными ?

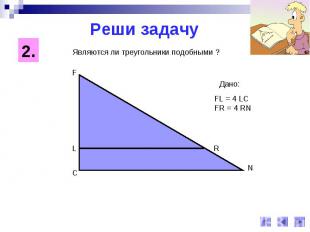
Реши задачуЯвляются ли треугольники подобными ?

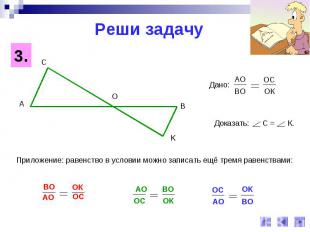
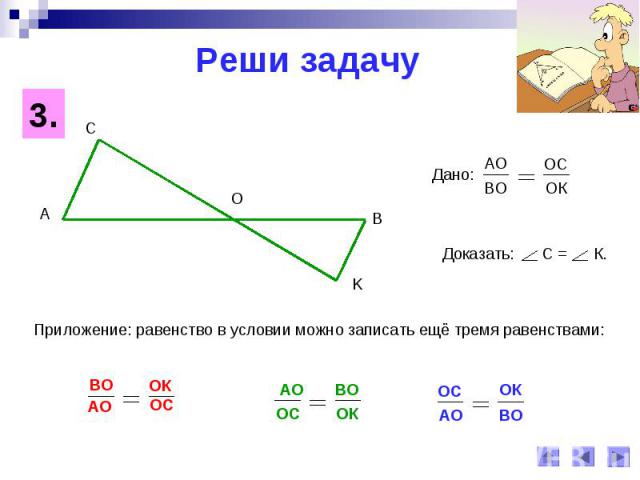
Реши задачуПриложение: равенство в условии можно записать ещё тремя равенствами:

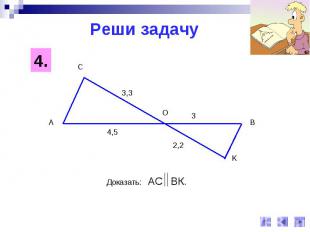
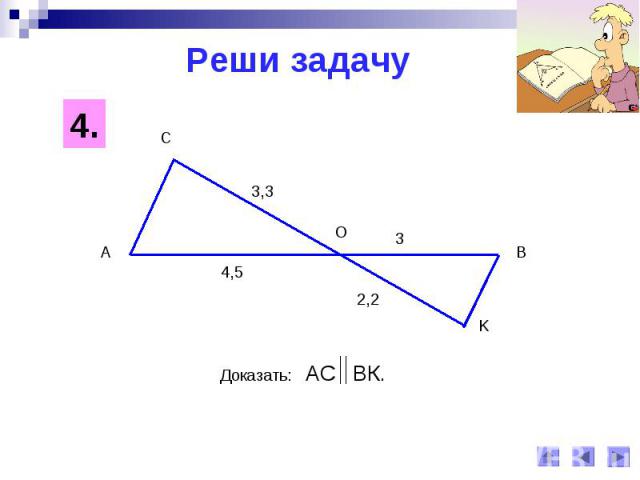
Реши задачуДоказать: АС ВК.

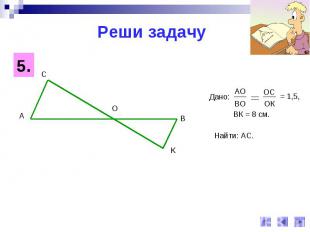
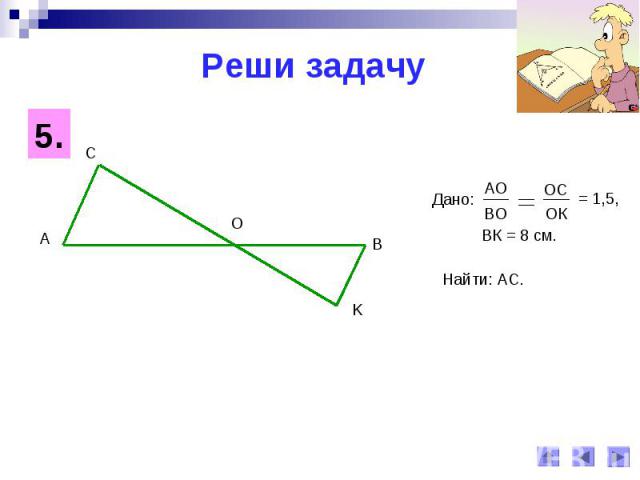
Реши задачу

Решение задачиДано: ОС = 5см, ОВ = 6 см, ОА = 15 см, ОК = 18 см.Доказать: АВСК – трапеция.Найти: SАОК : SСОВ.Рассмотрим АОК и СОВ, АОК = ВОС по свойству вертикальных углов.по второму признаку подобия, коэффициент подобия k = 3.По теореме об отношении площадей подобных треугольников SАОК : SСОВ = k2 Из подобия треугольников следует, что ОАК = ОСВ, а они – накрестлежащие при прямых АК и ВС (секущая АС), значит, АК ВС,следовательно, АВСК – трапеция.

Желаю успехов в учёбе!Михайлова Л. П.ГОУ ЦО № 173.