Презентация на тему: Две прямые, параллельные третьей прямой

Две прямые, параллельные третьей прямой
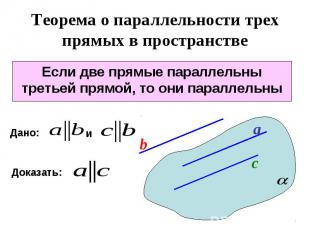
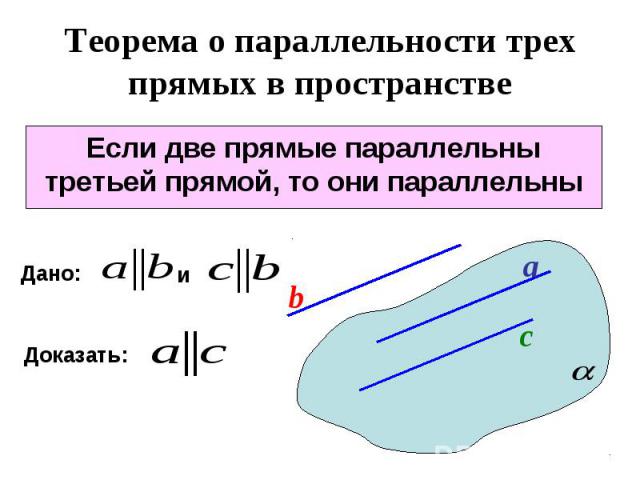
Теорема о параллельности трех прямых в пространстве Если две прямые параллельны третьей прямой, то они параллельны
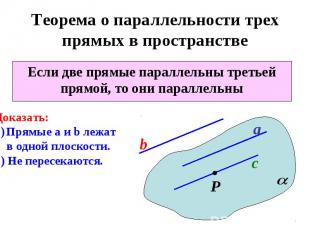
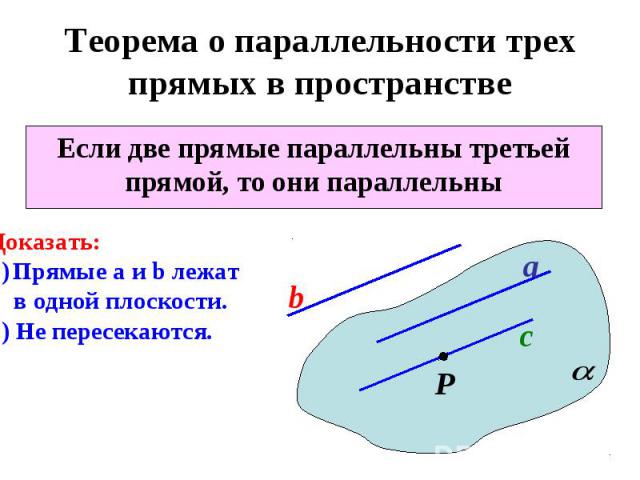
Теорема о параллельности трех прямых в пространствеЕсли две прямые параллельны третьей прямой, то они параллельныДоказать:Прямые а и b лежат в одной плоскости.2) Не пересекаются.

Теорема. Две прямые, параллельные третьей прямой, параллельны.Лемма. Если одна из параллельных прямых пересекает плоскость, то и другая пересекает эту плоскостьДано: а || b; a = A. Доказать: b = B.Доказательство. 1) ! | а и b 2) A и A = c | Ac; 3) : a c = A, а || b b c = B; 4) B, b, значит, b = B.

Две прямые, лежащие в одной плоскости, и не имеющие общих точек, называются параллельнымиДоказательство от противного.

Дано: а || c; b || c. Доказать: a || b.ДоказательствоПредположим, что а b = O, тогда Оа, а || c и Оb, b || c – противоречие с доказанной теоремой, то есть, а b = .2) Предположим, что а и b не лежат в одной плоскости. Рассмотрим Аа, тогда ! | А и b, причем, a = A. По лемме, так как с || a, то c = C | Cb, поскольку с || b.Следовательно, с b– противоречие.Таким образом, a, b и а b = , то есть, а || b.
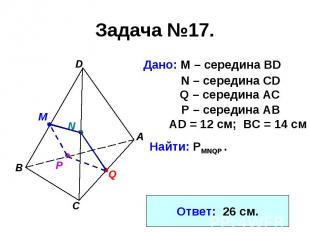
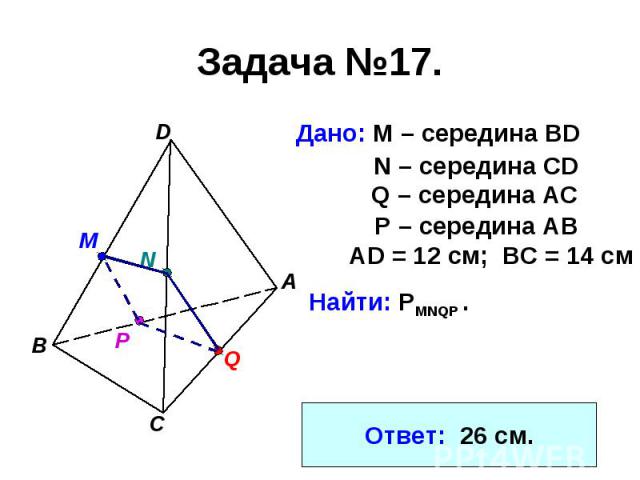
Задача №17.Дано: М – середина BD Найти: PMNQP .Ответ: 26 см.
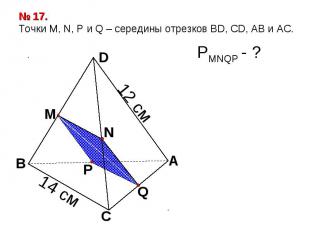
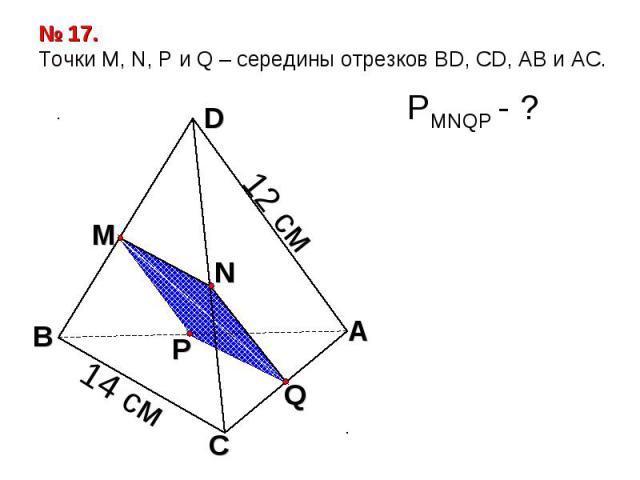
№ 17. Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
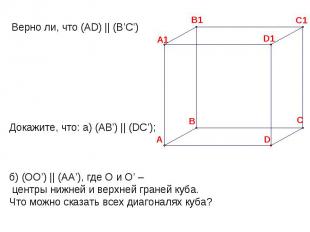
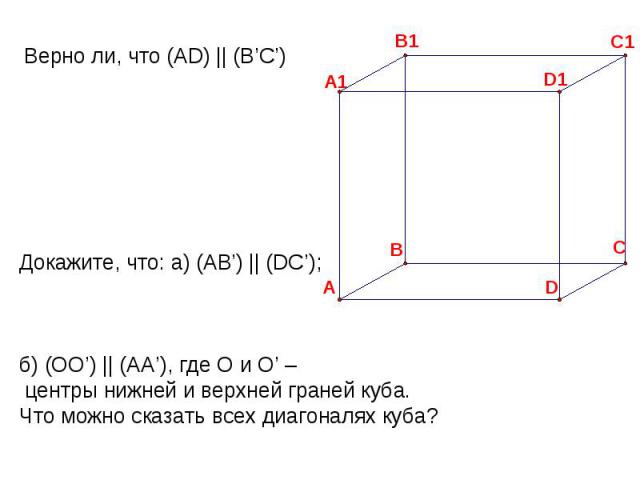
Верно ли, что (AD) || (B’C’) Докажите, что: а) (AB’) || (DC’); б) (OO’) || (AA’), где О и О’ – центры нижней и верхней граней куба.Что можно сказать всех диагоналях куба?