Презентация на тему: Паркеты на плоскости

Паркеты на плоскости

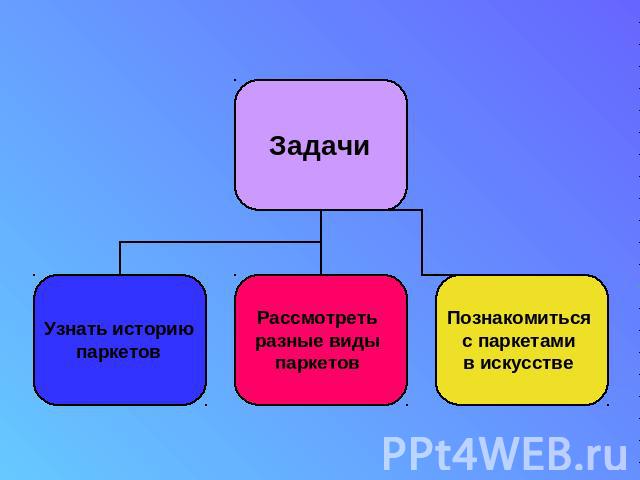
Цель работы – подробно изучить паркеты.

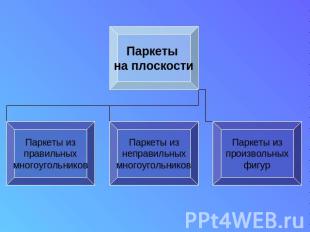
Паркеты

Паркет называется правильным, если он состоит из равных правильных многоугольников.

Паркет из квадратов

Простой паркет из правильных треугольников.

Паркет из правильных шестиугольников
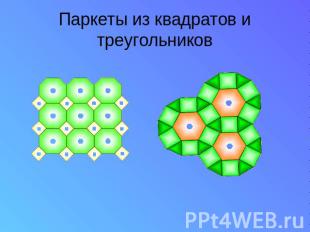
Паркеты из квадратов и треугольников

В одной вершине сходятся три правильных треугольника и два квадрата.

В одной вершине сходятся четыре треугольника и шестиугольник.

В одной вершине сходятся два треугольника и два шестиугольника.

Паркет, состоящий из квадратов и восьмиугольников

Паркет из треугольников и двенадцатиугольников.

В каждой вершине сходятся шестиугольник, треугольник и два квадрата.
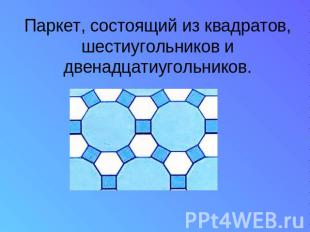
Паркет, состоящий из квадратов, шестиугольников и двенадцатиугольников.
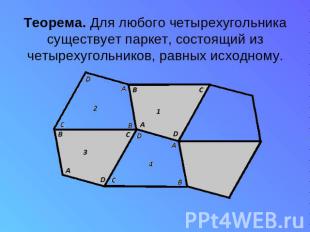
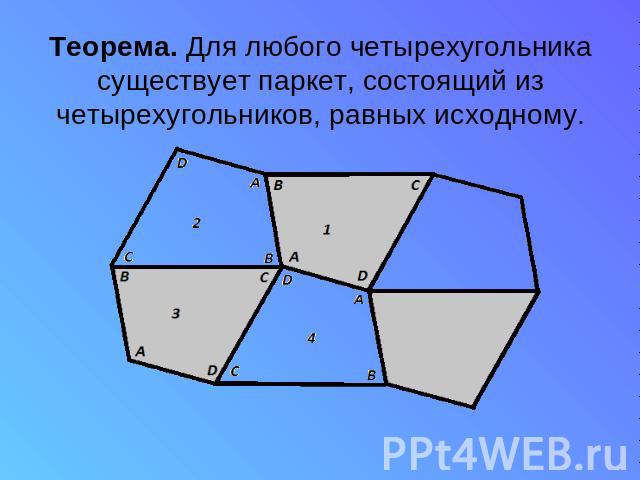
Теорема. Для любого четырехугольника существует паркет, состоящий из четырехугольников, равных исходному.

Паркет из параллелограммов.

Паркет из произвольных четырехугольников

Паркет из криволинейных плиток.

Спиральное замощение плоскости девятиугольниками

Квазипериодические паркеты

Мариус Корнелис Эшер (1898-1972) Он оставил потомкам 448 литографий и гравюр, более 2000 картин и набросков.

Работы Мариуса Эшера: «Ящерицы» «Летящие птицы» «Всадники»