Презентация на тему: Ортотреугольник и его свойства

Муниципальное общеобразовательное учреждение«Лицей № 230» Ортотреугольники его свойства Работу выполнилаученица 9 «А» класса МОУ «Лицей» № 230Волкова Екатерина Евгеньевна.Руководитель:Редкина Елена Ивановна г.Заречный, Пензенская область2008 г.

Италия, начало XVIII века Инженер и математик Фаньяно Дей Тоски (1682—1766) Задача: вписать в данный остроугольный треугольник ABC треугольник наименьшего периметра так, чтобы на каждой стороне треугольника ABC лежала одна вершина треугольника. Существует единственный вписанный треугольник наименьшего периметра - ортотреугольник.

Цель данной работы:описание дополнительных геометрических свойств треугольника. Задачи:1) выяснить, что такое ортотреугольник;2) изучить его свойства;3) рассмотреть возможное применение этих свойств к решению задач.

Определение ортотреугольника

Свойства ортотреугольника Ортотреугольник отсекает треугольники, подобные данному.Две смежные стороны ортотреугольника образуют равные углы с соответствующей стороной исходного треугольника.3. Высоты треугольника являются биссектрисами ортотреугольника. 4. Ортотреугольник – это треугольник с наименьшим периметром, который можно вписать в этот треугольник .5. Периметр ортотреугольника равен удвоенному произведению высоты треугольника на синус угла, из которого она исходит.

2.1 Теорема о подобии треугольников Ортотреугольник отсекает треугольники, подобные данному.

2.2 Теорема о свойстве биссектрис ортотреугольника

2.3 Теорема Фаньяно Среди всех треугольников, вписанных в данный остроугольный треугольник, наименьший периметр имеет ортотреугольник.

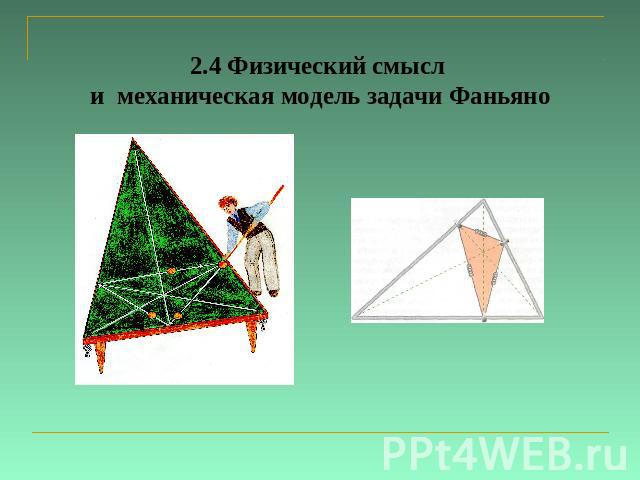
2.4 Физический смысл и механическая модель задачи Фаньяно

2.5 Периметр ортотреугольника

Задача 1. Пусть и – высоты треугольника АВС. Докажите, что треугольник подобен треугольнику АВС. Чему равен коэффициент подобия?

Задача 3. В остроугольном треугольнике АВС проведены высоты АD, ВЕ и СF.Докажите, что pR=Pr, где p-периметр треугольника EDF, Р – периметр треугольника АВС.

Задача 5. В равнобедренном треугольнике ABC с основанием AC = 4 и боковой стороной AB = 8 проведены высоты . Найти периметр треугольника и длину высоты .