Презентация на тему: Иоганн Кеплер

Иоганн Кеплер (1571-1630) Немецкий астроном и математик. Один из создателей современной астрономии - открыл законы движения планет (законы Кеплера), заложил основы теории затмений, изобрел телескоп, в котором объектив и окуляр – двояко-выпуклые линзы.

Модели И.Кеплера Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.

Многогранники

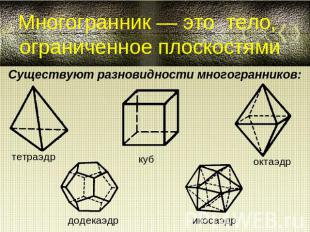
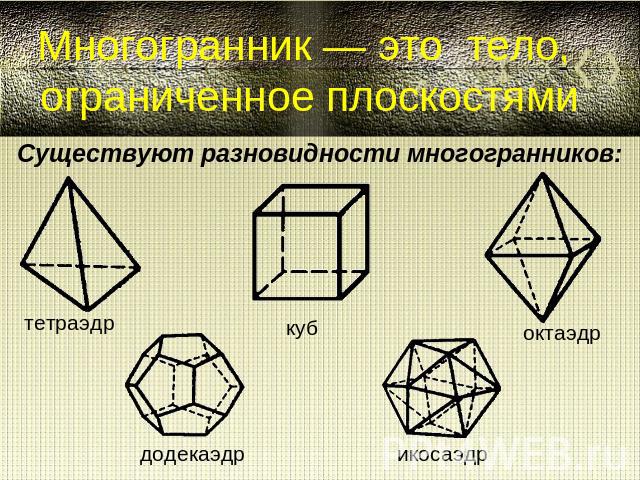
Многогранник — это тело, ограниченное плоскостями Существуют разновидности многогранников:

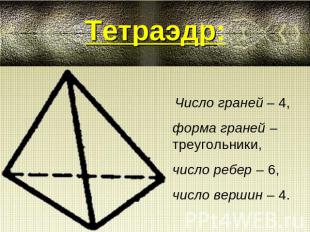
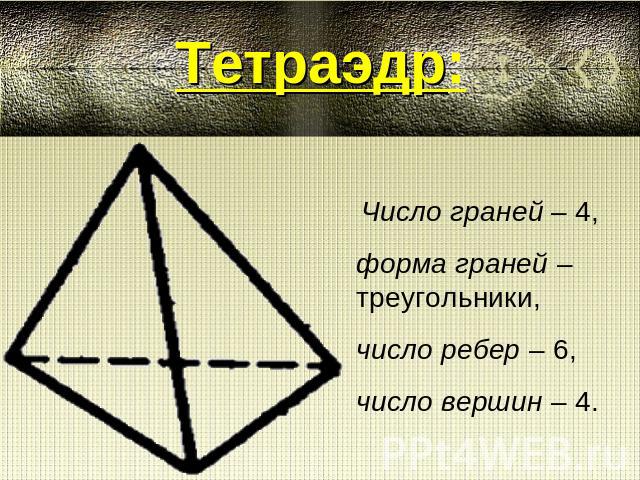
Тетраэдр: Число граней – 4, форма граней – треугольники, число ребер – 6, число вершин – 4.

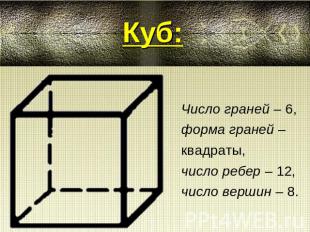
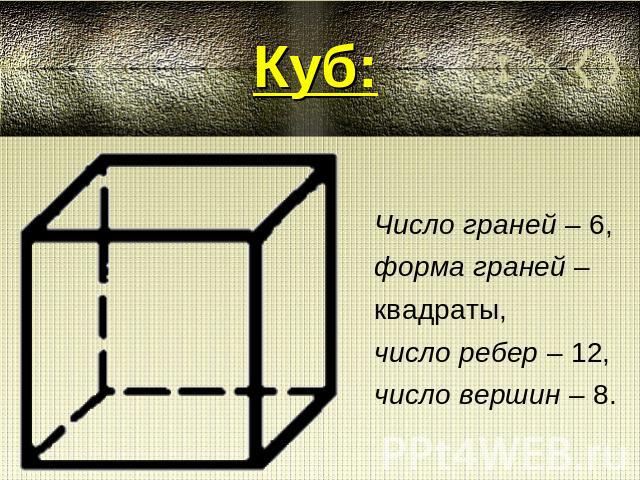
Куб: Число граней – 6,форма граней – квадраты,число ребер – 12, число вершин – 8.

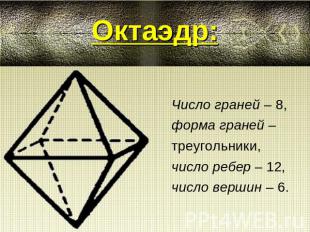
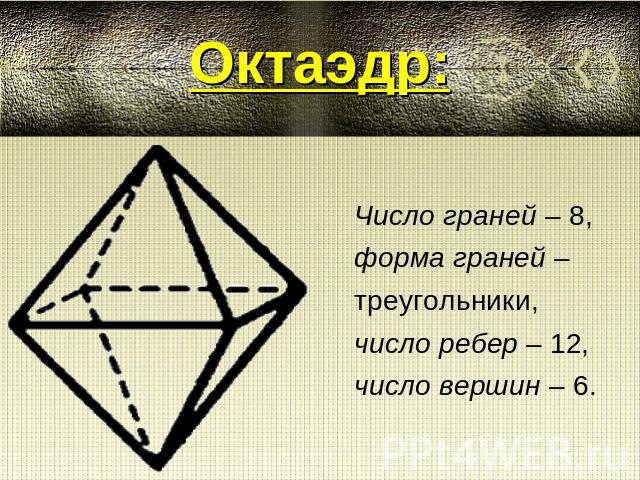
Октаэдр: Число граней – 8,форма граней – треугольники, число ребер – 12, число вершин – 6.

Додекаэдр:Число граней – 12, форма граней – пятиугольники,число ребер – 30, число вершин – 20.

Икосаэдр:Число граней – 20, форма граней –треугольники,число ребер – 30, число вершин – 12.

Как и любые другие тела, многогранники имеют ОБЪЁМ! Его можно измерить с помощью выбранной единицы измерения объёма: кубический сантиметр (см3) кубический метр (м3) кубический миллиметр (мм3) и т.д.

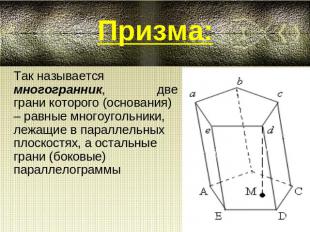
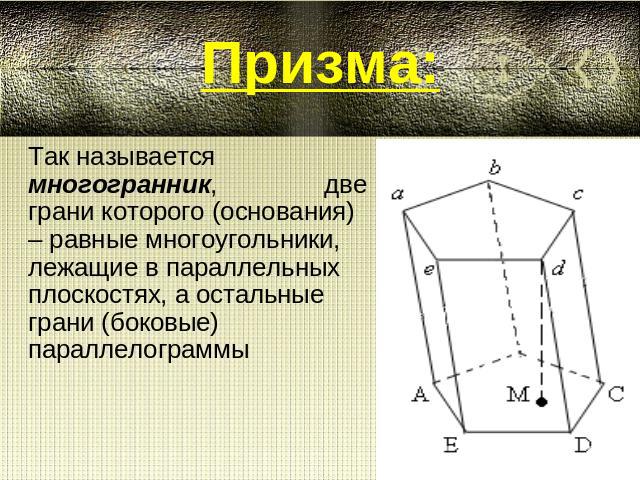
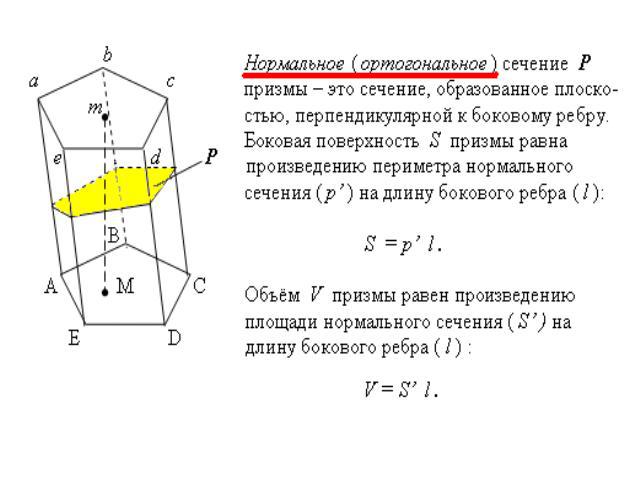
Призма:Так называется многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а остальные грани (боковые) параллелограммы

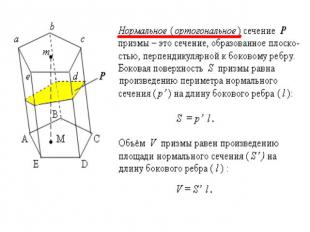
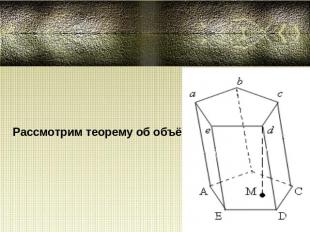
Рассмотрим теорему об объёме призмы:

Прямоугольный параллелепипед: прямой параллелепипед, основания которого – прямоугольники.У него все диагонали равны.Квадрат диагонали равен сумме квадратов ребёр, исходящих из одной вершины:d2 = a2 + b2 + c2.Sполн = 2 (ab + bc + ac); V = abc

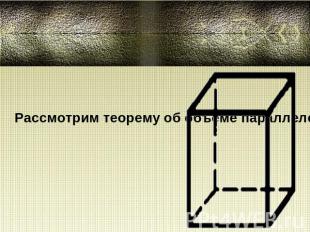
Рассмотрим теорему об объёме параллелепипеда:

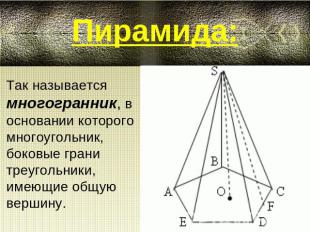
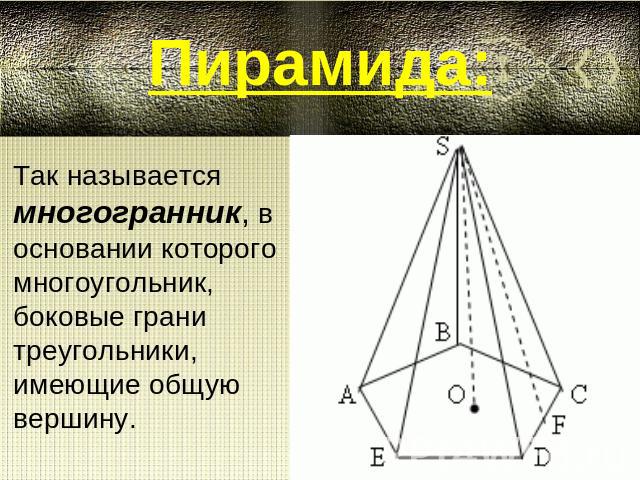
Пирамида:Так называется многогранник, в основании которого многоугольник, боковые грани треугольники, имеющие общую вершину.

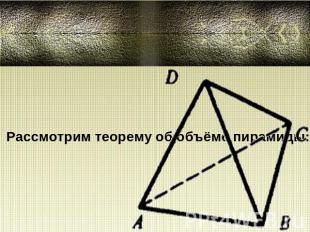
Рассмотрим теорему об объёме пирамиды:

Общий итог: Итак, нас окружают разнообразные тела. Каждое из них имеет свой объем.Я показала основные конфигурации объёмных тел, которые дают представление об их формах. Внешний вид тел различен, но в основе лежат основные фигуры, представленные в этой презентации.

Презентацию подготовила:ученица 10 «Б» классашколы № 1242Алексеева Маргарита