Презентация на тему: Круги Эйлера (6 класс)

Круги Эйлера Работу выполнил ученик 6 класса Руководитель :Учитель математики Кемаева Галина Серафимовна

Цель исследования:изучение биографии Л. Эйлераизучение способа решения задач с помощью кругов Эйлера;Задачи исследования:Познакомится с кругами Эйлера, кругами (диаграммами) Эйлера – Венна.Составлять и решать подобные задачи

Биография Леонарда Эйлера Леонард Эйлер (15) апреля 1707, Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — российский и швейцарский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. В 1726 году он был приглашён работать в Санкт-Петербург. В 1731—1741 и, начиная с 1766 года, был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском.

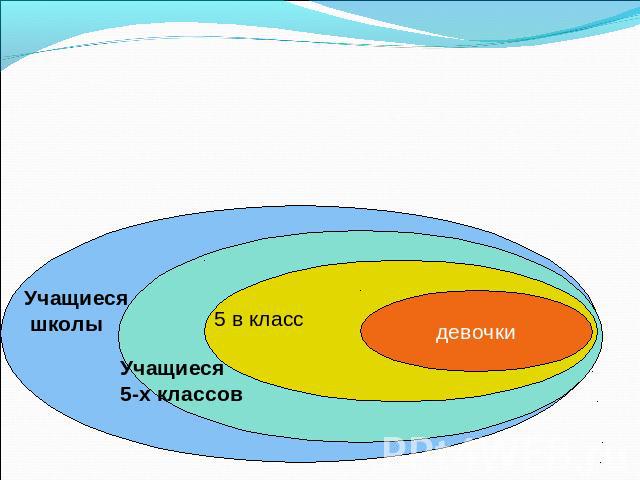
Типы кругов Эйлера Этот метод даёт ещё более наглядное представление о возможном способе изображения условий, зависимости, отношений в логических задачах.

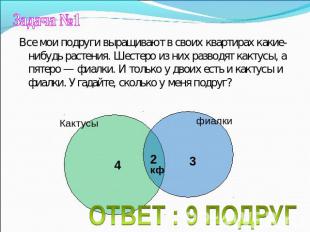
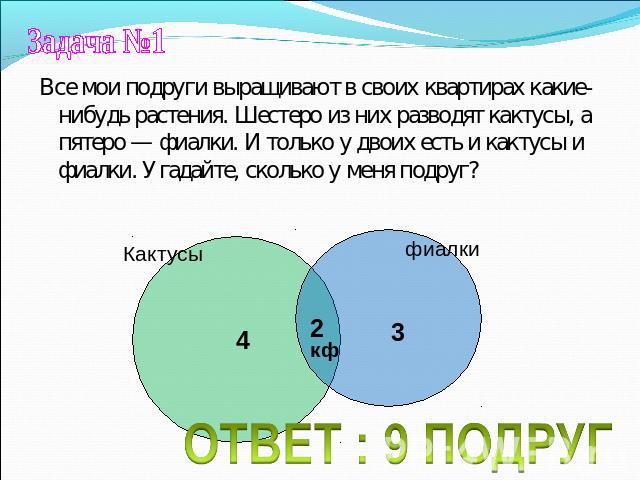
Задача №1 Все мои подруги выращивают в своих квартирах какие-нибудь растения. Шестеро из них разводят кактусы, а пятеро — фиалки. И только у двоих есть и кактусы и фиалки. Угадайте, сколько у меня подруг? ОТВЕТ : 9 ПОДРУГ

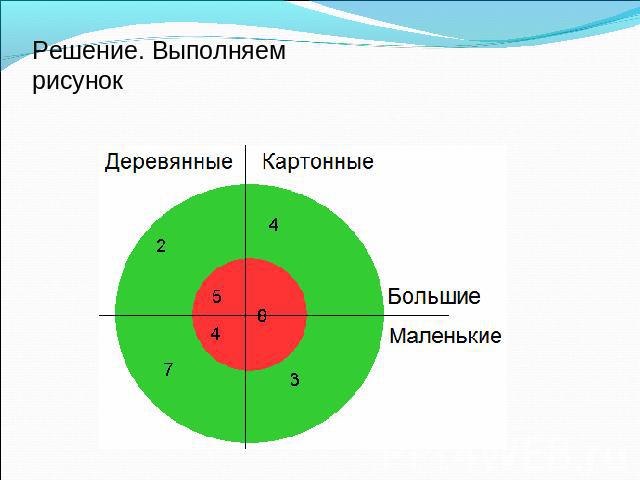
Задача, решаемая с помощью диаграммы Эйлера – Венна. Ребятам поручили изготовить кубики. Несколько кубиков сделали из картона, а остальные из дерева. Кубики были двух размеров: большие и маленькие. Часть из них покрасили в зеленый цвет, другую – в красный. Получилось 16 зеленых кубиков. Зеленых кубиков большого размера было 6. Больших зеленых из картона было 4. Красных кубиков из картона было 8,красных кубиков из дерева – 9. Больших деревянных кубиков было 7, а маленьких деревянных кубиков было 11. Сколько же всего получилось кубиков?

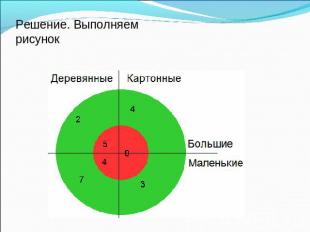
Решение. Выполняем рисунок

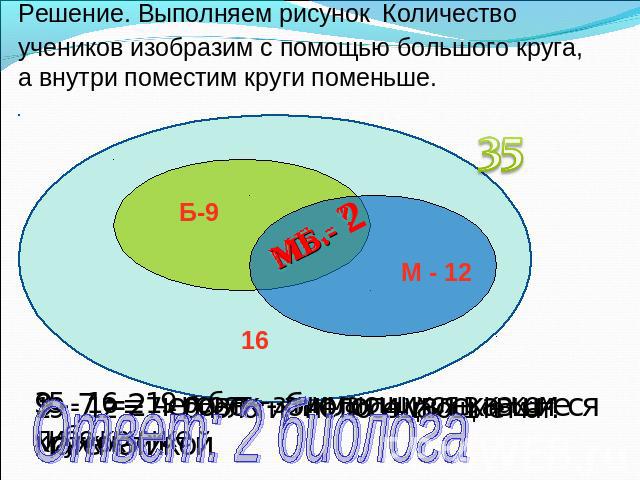
В классе 35 учеников. В математическом кружке из них 12 занимаются, в биологическом - 9, а 16 ребят не посещают эти кружки. Сколько биологов увлекаются математикой.

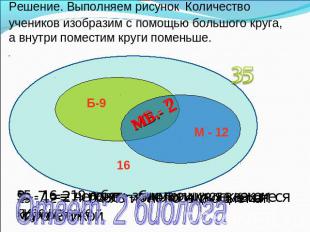
Решение. Выполняем рисунок Количество учеников изобразим с помощью большого круга, а внутри поместим круги поменьше. Ответ: 2 биолога 19 - 12 = 7 - биологи, не посещающие мат. кружок

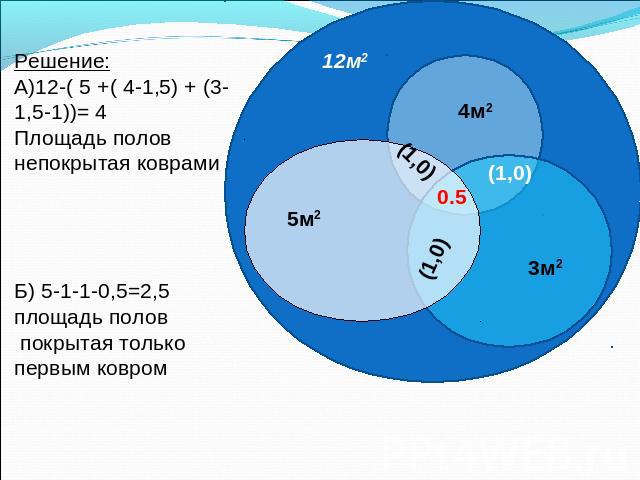
На полу площадью 12м2 лежат три ковра: площадь одного 5м2, другого - 4м2 и третьего - 3м2. Каждые два ковра перекрываются на площади 1,5м2, причем 0,5м2 из этих полутора квадратных метров приходится на участок пола, где перекрываются все три ковра. а) Какова площадь пола, не покрытая коврами? б) Какова площадь пола, покрытая одним только первым ковром?

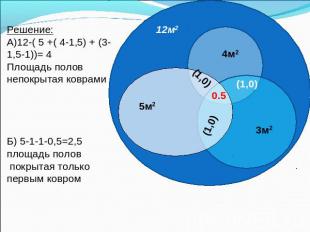
Решение:А)12-( 5 +( 4-1,5) + (3-1,5-1))= 4 Площадь полов непокрытая коврамиБ) 5-1-1-0,5=2,5 площадь полов покрытая только первым ковром

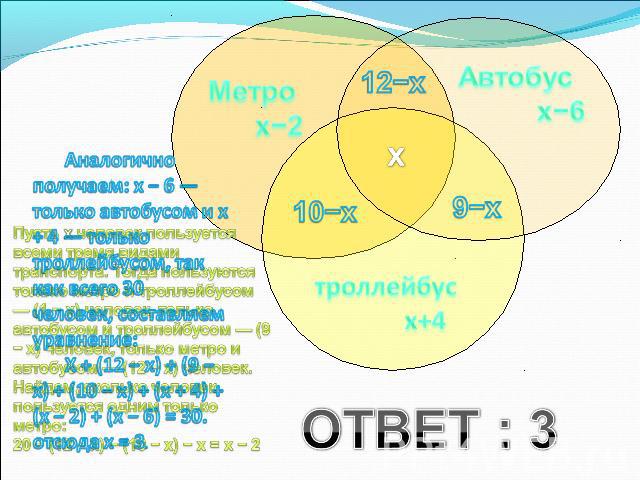
Всего – 30 человекПользуются метро – 20 человекАвтобусом – 15 человекТроллейбусом – 23 человекаМетро и троллейбусом – 10 человекМетро и автобусом – 12 человекТроллейбусом и автобусом – 9Сколько человек ежедневно пользуются всеми тремя видами транспорта?

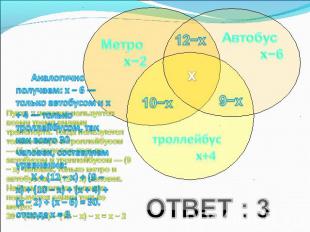
Аналогично получаем: х − 6 — только автобусом и х + 4 — только троллейбусом, так как всего 30 человек, составляем уравнение:Х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30. отсюда х = 3. Пусть х человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом — (1 − х) человек, только автобусом и троллейбусом — (9 − х) человек, только метро и автобусом — (12 − х) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х) − (10 − х) − х = х − 2

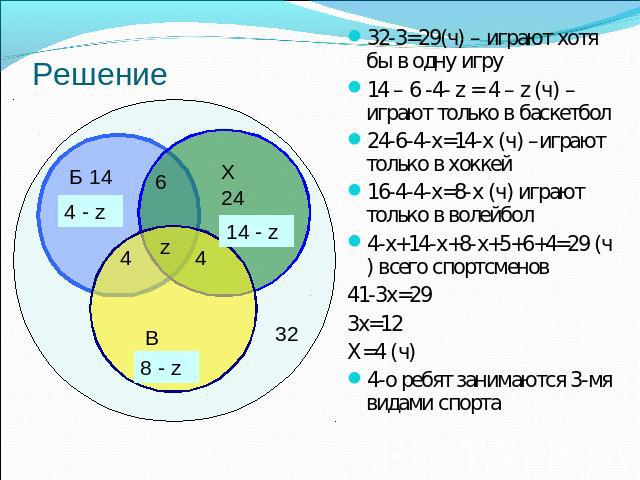
Всего- 32 челБаскетбол - 16 челХоккей - 24 челВолейбол - 16 челБ.Х - 6 челБ.В - 4 челВ.Х - 4 челНи чем– 3 челСколько человек занимаются всеми видами спорта? В одной спортивной секции?

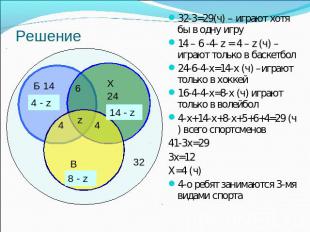
32-3=29(ч) – играют хотя бы в одну игру14 – 6 -4- z = 4 – z (ч) –играют только в баскетбол24-6-4-х=14-х (ч) –играют только в хоккей16-4-4-х=8-х (ч) играют только в волейбол4-х+14-х+8-х+5+6+4=29 (ч) всего спортсменов41-3х=293х=12Х=4 (ч) 4-о ребят занимаются 3-мя видами спорта

Ты человек, а значит, тыОбязан рассуждать –А без логичной простотыТы будешь пропадать.Пусть за собой она зовёт –Уйми в коленях дрожь!Коль с Логикой пойдёшь вперёд –Нигде не пропадёшь!(С. Алдошин)

Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными.

Выводы:Для решения задач, решаемых с помощью кругов Эйлера, был составлен алгоритм, состоящий из следующих этапов:Записываем краткое условие задачи.Выполняем рисунок.Записываем данные в круги (или в диаграмму Эйлера).Выбираем условие, которое содержит больше свойств.Анализируем, рассуждаем, не забывая записывать результаты в части круга (диаграммы).Записываем ответ.

спасибо за внимание!