Презентация на тему: Множества. Операции над множествами. Круги Эйлера

На языке мудрости ЗНАТЬ – это значит УМЕТЬ, а ПОНИМАТЬ – это значит ДЕЙСТВОВАТЬ.

Тема урока: Множества. Операции над множествами. Круги Эйлера.

Цель урока: обобщить и систематизировать знания студентов по теме: «Множества. Операции над множествами. Круги Эйлера.»

МНОЖЕСТВО ЭЛЕМЕНТ МНОЖЕСТВА ВИДЫ МНОЖЕСТВ ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ ОБЪЕДИНЕНИЕ МНОЖЕСТВ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ НАХОДИТЬ ОБЪЕДИНЕНИЕ МНОЖЕСТВ НАХОДИТЬ ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ ИЗОБРАЖАТЬ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА-ВЕННА РЕШАТЬ ЗАДАЧИ С ИСПОЛЬЗОВАНИЕМ ИМЕЮЩИХСЯ ЗНАНИЙ

основатель теории множеств Георг Кантор (1845 -1918 гг.) – немецкий математик «Множество есть многое, мыслимое нами как единое»

Понятие теории множеств Понятие множества является одним из наиболее общих и наиболее важных математических понятий. Оно было введено в математику немецким ученым Георгом Кантором (1845-1918).Следуя Кантору, понятие "множество" можно определить так: Множество-совокупность объектов, обладающих определенным свойством, объединенных в единое целое.

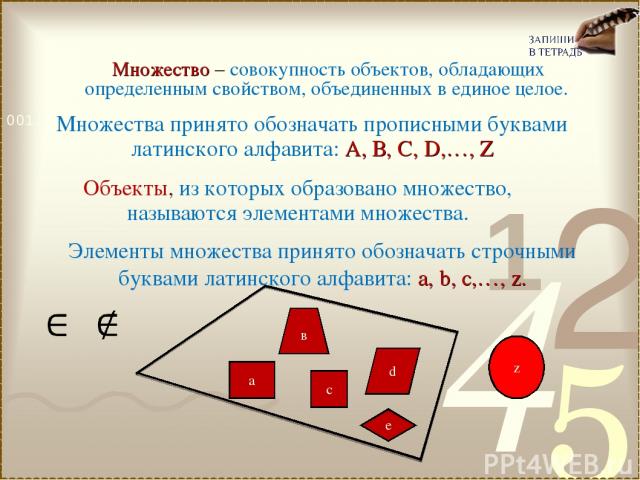
Множество – совокупность объектов, обладающих определенным свойством, объединенных в единое целое. Объекты, из которых образовано множество, называются элементами множества. Множества принято обозначать прописными буквами латинского алфавита: А, В, С, D,…, Z е в d а с z Элементы множества принято обозначать строчными буквами латинского алфавита: а, b, c,…, z.

множество людей на Солнце множество прямых углов равностороннего треугольника множество точек пересечения двух параллельных прямых Пустое множество-множество, не содержащее ни одного элемента.

КОЛЛЕКЦИЯ МАРОК НАБОР КАРАНДАШЕЙ СТАЯ ПТИЦ ЧАЙНЫЙ СЕРВИЗ БУКЕТ ЦВЕТОВ СТАДО КОРОВ

Множество четырехугольников Пространственные тела 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11… Квадраты чисел Цифры десятичной системы счисления 10, 12, 14, 16 … 96, 98 множество элемент Трапеция, параллелограмм, ромб, квадрат, прямоугольник Шар, прямоугольный параллелепипед, призма, пирамида, октаэдр Натуральные числа 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 .. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двузначные четные числа

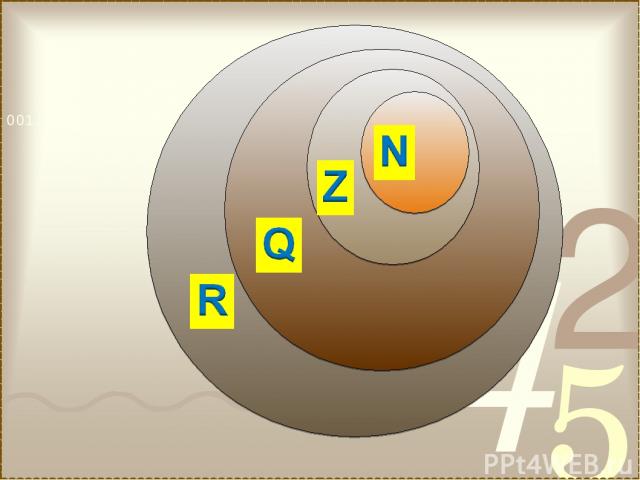
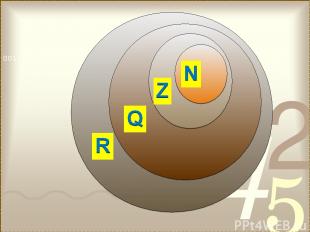
Обозначения числовых множеств N – множество натуральных чисел; Z – множество целых чисел; Q – множество рациональных чисел; R – множество действительных чисел.

Стандартные обозначения

Запишите множества букв слов КОНИ И КИНО ВИДЫ МНОЖЕСТВ Равные множества {К, О, Н, И} {К, И, Н, О}

А = {2; 3; 5; 7; 11; 13}; {х | 5< х

{1; 4; 9; 16; 25; …}; {10; 20; 30; 40; 50; …}; ВИДЫ МНОЖЕСТВ Бесконечные множества

Среди перечисленных ниже множеств укажите конечные и бесконечные множества: а) множество чисел, кратных 13; б) множество делителей числа 15; в) множество деревьев в лесу; г) множество натуральных чисел; д) множество рек Ростовской области; е) множество корней уравнения х + 3 = 11; ж) множество решений неравенства х + 1 < 3.

Задайте множество цифр, с помощью которых записывается число: а) 3254; б) 8797; в) 11000; г) 555555. Охарактеризуйте множество А: а) А = {1, 3, 5, 7, 9}; б) А = {- 2, - 1, 0, 1, 2}; в) А = {11, 22, 33, 44, 55, 66, 77, 88, 99}.

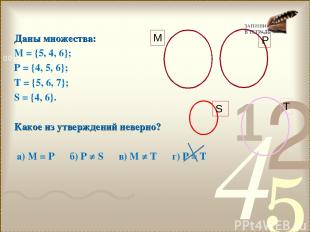
Даны множества: М = {5, 4, 6}; Р = {4, 5, 6}; Т = {5, 6, 7}; S = {4, 6}. Какое из утверждений неверно? а) М = Р б) Р ≠ S в) М ≠ Т г) Р = Т

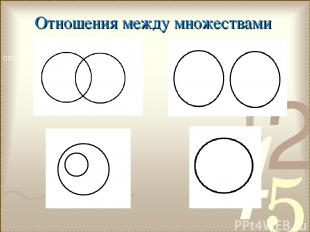
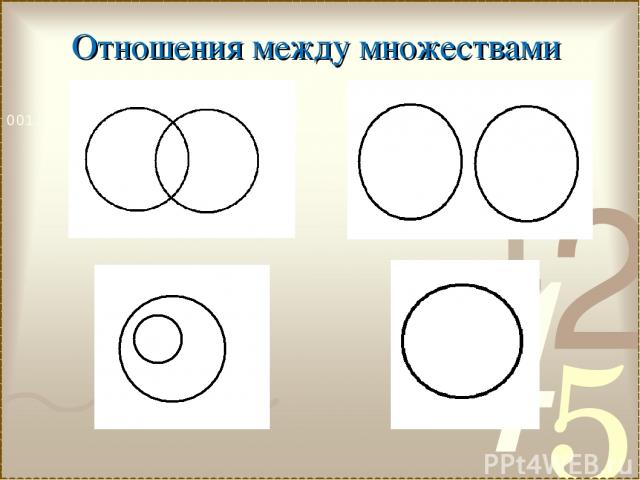
Отношения между множествами

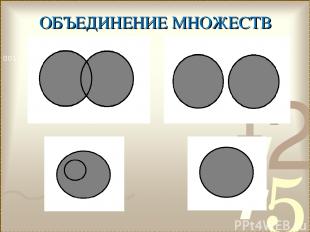
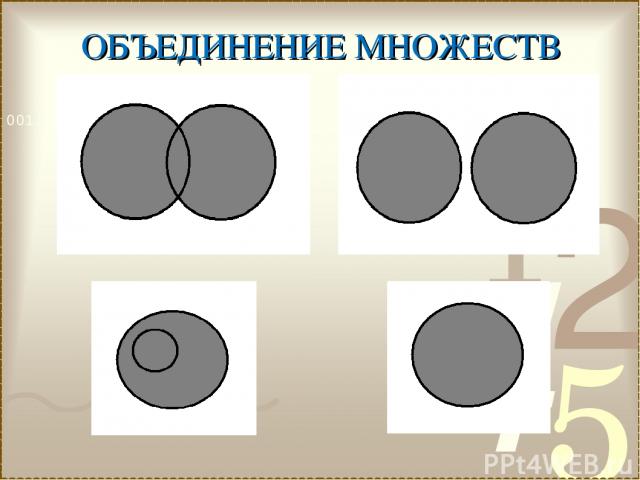
ОБЪЕДИНЕНИЕ МНОЖЕСТВ

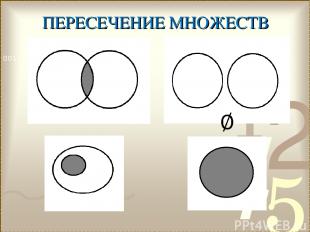
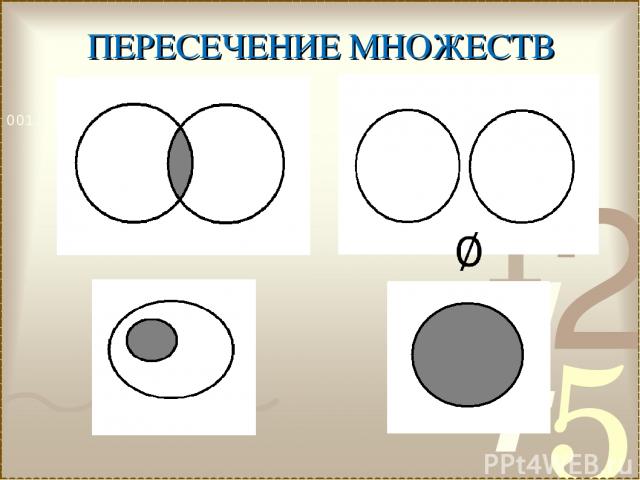
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ

Даны множества: А = {2; 3; 8}; В = {2; 3; 8; 11}; С = {5; 11}. Найдите: 1) АUВ; 2) АUС; 3) СUВ.

Даны множества: А = {a, b, c, d}; B = {c, d, e, f}; C = {c, e, g, k}. Найдите: (АUВ)UС.

Даны множества: А – множество всех натуральных чисел, кратных 10; В = {1; 2; 3;…, 41}. Найдите А∩В.

k Решение задачи с помощью кругов Эйлера Леона рд Э йлер (1707-1783 гг.)  — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

поют 17 танцуют 19 Всего 30 17+19=36, всего 30 36-30=6 6 11 13 В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?

Решение Пусть А - это множество учеников, умеющих петь. Количество элементов в нём по условию равно n = 17. Пусть В - множество учеников, умеющих танцевать. Количество элементов в нём - m = 19. Множество совпадает со всем классом, т.к. каждый ученик в классе поёт или танцует. - это множество тех учеников класса, которые поют и танцуют одновременно. Пусть их количество равно k. Согласно формуле доказанной выше n + m- k = 17+ 19- k = 30 k = 6. Ответ: 6 учеников в классе поют и танцуют одновременно.

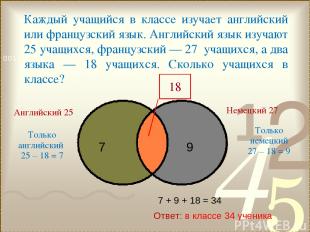
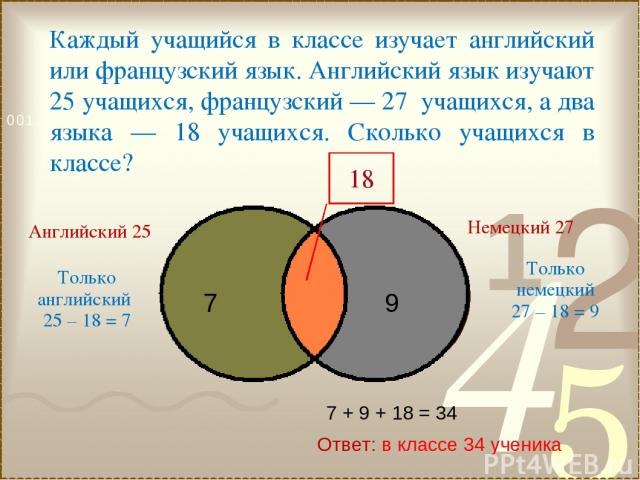
Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе? Ответ: в классе 34 ученика Английский 25 Немецкий 27 Только английский 25 – 18 = 7 Только немецкий 27 – 18 = 9 7 + 9 + 18 = 34 18 7 9

Расположите 4 элемента в двух множествах так, чтобы в каждом из них было по 3 элемента

Множества А и В содержат соответственно 5 и 6 элементов, а множество А ∩ В – 2 элемента. Сколько элементов в множестве А U В? Объединение содержит 9 элементов

Каждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь 13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме? * Всего: 14 + 13 + 62 =89

На школьной спартакиаде каждый из 25 учеников 9-го класса выполнил норматив или по бегу, или по прыжкам в высоту. Оба норматива выполнили 7 человек, а 11 учеников выполнили норматив по бегу, но не выполнили норматив по прыжкам в высоту. Сколько учеников выполнили норматив: а) по бегу; б) по прыжкам в высоту; в) по прыжкам при условии, что не выполнен норматив по бегу?

Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекаются коллекционированием? *

Каждый из учеников 9-го класса в зимние каникулы ровно два раза был в театре, посмотрев спектакли А, В или С. При этом спектакли А, В, С видели соответственно 25, 12 и 23 ученика. Сколько учеников в классе?

В воскресенье 19 учеников нашего класса побывали в планетарии, 10 – в цирке и 6 – на стадионе. Планетарий и цирк посетили 5 учеников; планетарий и стадион - 3; цирк и стадион - 1. Сколько учеников в нашем классе, если никто не успел посетить все три места, а три ученика не посетили ни одного места?

САМООЦЕНКА 10 – хорошо знаю весь фактический материал, и участвовал в организации группы; 9 – хорошо  знаю свой вопрос, и участвовал в работе на уроке; 8 – хорошо знаю весь фактический материал; 7 – хорошо  знаю свой вопрос; 6 – знаю свой вопрос; 5 – знаю свой вопрос, но был пассивен; 4 – плохо знаю свой вопрос, но был активен в обсуждении других вопросов; 3 – плохо знаю свой вопрос, и был пассивен; 1,2 – не знаю свой вопрос, и был пассивен.  

Подведение итогов занятия - оценка степени реализации поставленных целей; - оценка работы студентов; - самооценка работы студентов в группах.

Домашнее задание М.С. Спирина, «Дискретная математика» §§1.1.-1.2, с.14-20.

Спасибо за работу на уроке, урок окончен!