Презентация на тему: Множество. Операции над множествами

Введение в теорию множеств 1. Основные определения, терминология Под множеством А мы понимаем совокупность объектов произвольной природы, объединенных общим свойством Р(х). Обозначение Указанием определяющего свойства Перечислением элементов Пример 1 Иногда второе обозначение распространяется и на некоторые бесконечные множества. Так, N={1,2,3,...,n,...} Z={...,-n,...,-2,-1,0,1,2,...,n,...}.

Определение 1 Определение 1 Множество А называется подмножеством В, если для любого х ( ) Обозначение: Другими словами, символ " " есть сокращение для высказывания Теорема 1 Для любых множеств А, В, С верно следующее: а) ; б) и .

Определение 2 Определение 2 Множества А и В называются равными, если они состоят из одних и тех же элементов (A=В). Другими словами, обозначение А=В служит сокращением для высказывания Пример Указать равные множества A={0;1;2}, B = {1;0;2}, C={0;1;2;0}, D={{1;2};0}, E={1;2}, F={x:x3-3x2+2x=0}.

Определение 3 Определение 3 Множество называется пустым, если оно не содержит ни одного элемента, то есть х не принадлежит этому множеству (для любого х). Обозначение: .

2. Операции над множествами 2. Операции над множествами Определение 1 Объединением двух множеств А и В называется множество Пример Пусть А={1,2,3,4}, B={2,4,6,8}, тогда = {1,2,3,4,6,8}.

Объединение множеств Теорема 1 Пусть А, В, С – произвольные множества. Тогда: а) – идемпотентность объединения; б)   – коммутативность объединения; в)   – ассоциативность объединения; г) ; д)

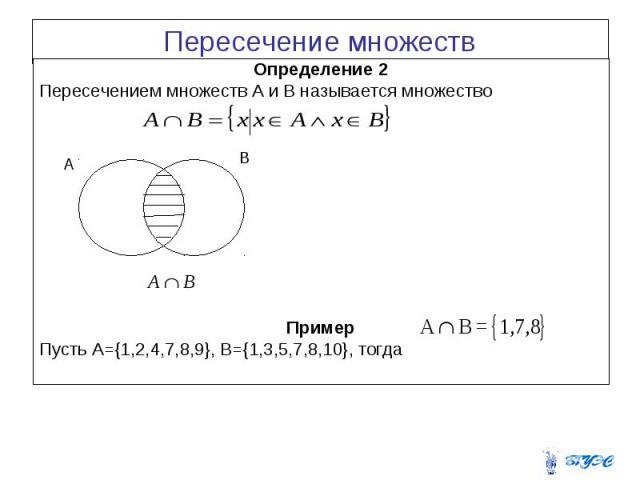
Пересечение множеств Определение 2 Пересечением множеств А и В называется множество Пример Пусть A={1,2,4,7,8,9}, B={1,3,5,7,8,10}, тогда

Пересечение множеств Теорема 2 Пусть А, В, С – произвольные множества, тогда: а) - идемпотентность пересечения; б) - коммутативность пересечения; в) - ассоциативность пересечения; г)

Объединение и пересечение множеств Теорема 3 1) 2) 3) 4)

Разность множеств, дополнение, симметрическая разность Разность множеств, дополнение, симметрическая разность Определение 3 Разностью множеств A и B называется множество . Пример Пусть А={1,3,4,7,8,9,10}, B={2,3,4,5,6,7}, тогда A\B={1,8,9,10}, B\A={2,5,6}.

Разность множеств Теорема 4 Пусть А, В, С – произвольные множества, тогда: 1) 2) 3) 4) Теорема 5 (законы Моргана) а) б)

Множество U назовем "универсальным", если оно содержит все элементы и все множества являются его подмножествами. Понятие "универсального множества" у нас будет зависеть от круга задач, которые мы рассматриваем. Довольно часто под универсальным множеством понимают множество R –– множество вещественных чисел или множество С – комплексных чисел. Возможны и другие примеры. Всегда в контексте необходимо оговорить, что мы понимаем под универсальным множеством U.

Дополнение множеств Определение 4 Пусть U – универсальное множество. Дополнением А в U (или просто дополнением А) называется множество . Пример Если U – множество вещественных чисел и А – множество рациональных чисел, то  – множество иррациональных чисел

Дополнение множеств 1) 2) 3) Законы Моргана для дополнений а) ; б) .

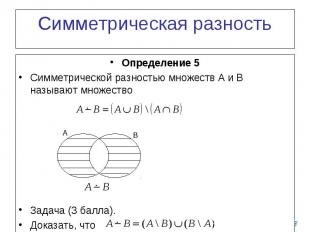
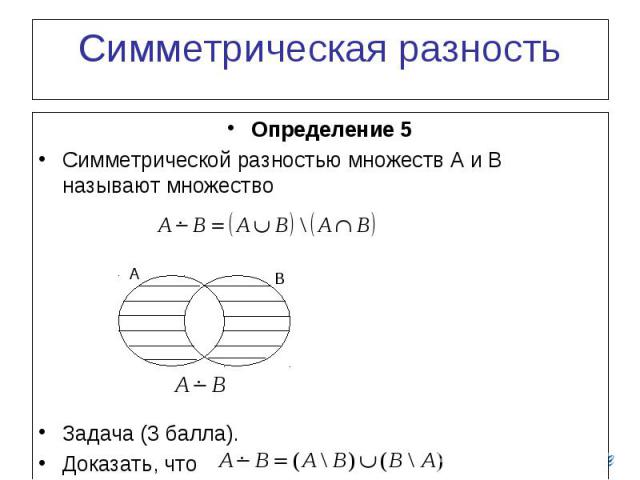
Симметрическая разность Определение 5 Симметрической разностью множеств A и B называют множество Задача (3 балла). Доказать, что

Вопросы: 1) Приведите пример множества, состоящего из 3 элементов. Опишите это множество свойством. 2) Перечислите все подмножества указанного множества. Чему равно их пересечение?