Презентация на тему: Множества и операции над ними

Множества и операции над ними

МНОЖЕСТВОЭЛЕМЕНТ МНОЖЕСТВАСПОСОБЫ ЗАДАНИЯ МНОЖЕСТВПОДМНОЖЕСТВОПЕРЕСЕЧЕНИЕ МНОЖЕСТВОБЪЕДИНЕНИЕ МНОЖЕСТВВЫЧИТАНИЕ МНОЖЕСТВДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ

МНОЖЕСТВО Понятие множества — простейшее математическое понятие, оно не определяется, а лишь поясняется при помощи примеров: множество книг на полке, множество точек на прямой (точечное множество) и т. д. Множества принято обозначать прописными буквами латинского алфавита: A, B, C… Z.

Элементы множества Объекты, из которых образовано множество, называются элементами.Элементы множества принято обозначать строчными буквами латинского алфавита: a, b, c… z.Если элемент х принадлежит множеству М, то записывают х О М, если не принадлежит – x П MЕсли множество не содержит ни одного элемента, оно называется пустым и обозначается Æ или 0.

Способы задания множеств

Характеристическое свойство Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.Этот способ задания множеств является общим и для конечных множеств, и для бесконечных.«Множество А натуральных чисел, меньших 7»: А = {x | x Î N и x<7}

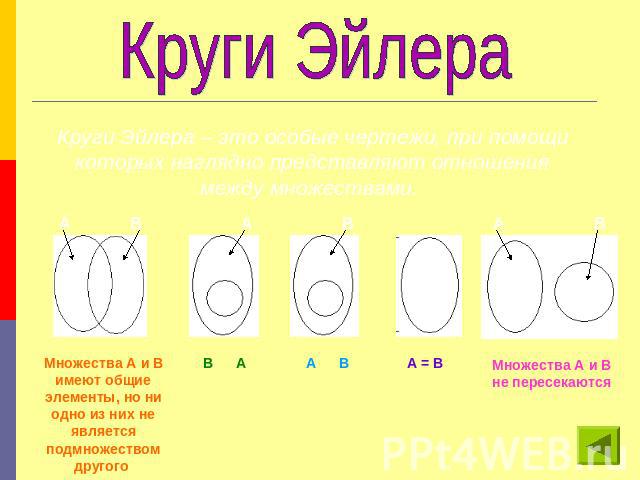
подмножествоМножество В является подмножеством множества А (В Ì А), если каждый элемент множества В является также элементом множества А. Пустое множество считают подмножеством любого множества. Любое множество является подмножеством самого себя.Отношения между множествами наглядно представляют при помощи кругов Эйлера

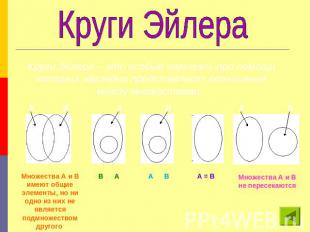
Круги ЭйлераКруги Эйлера – это особые чертежи, при помощи которых наглядно представляют отношения между множествами.

пересечение множествПересечение множеств — множество, состоящее из всех тех элементов, которые принадлежат одновременно всем данным множествам. Пересечение множеств А и В обозначают АÇВ.Если множества А и В не имеют общих элементов, то пишут: А З В = ЖХарактеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «и». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их пересечения обладают свойством: «быть четными натуральными и двузначными числами»

Объединение множествОбъединением множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В. Объединение множеств А и В обозначают А И ВХарактеристическое свойство формулируется путем соединения характеристических свойств пересекаемых множеств союзом «или». Например, если А – множество четных натуральных чисел, а В – двузначных чисел, то элементы их объединения обладают свойством: «быть четными натуральными и двузначными числами»

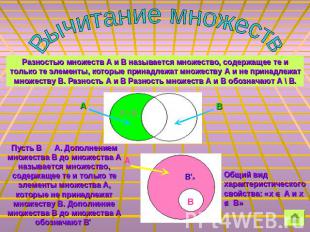
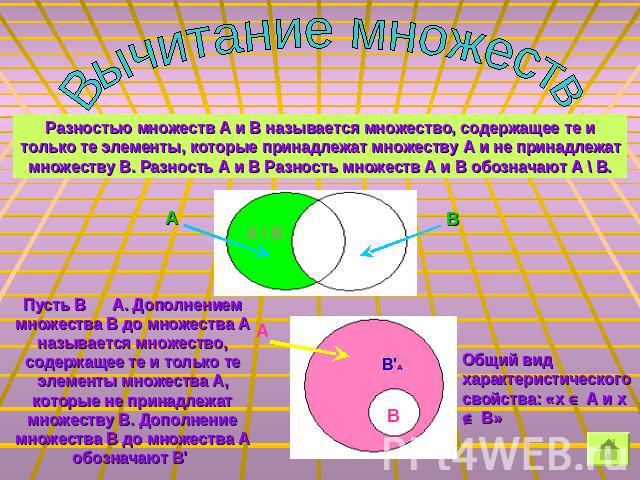
Вычитание множествРазностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. Разность А и В Разность множеств А и В обозначают А \ В.Пусть В М А. Дополнением множества В до множества А называется множество, содержащее те и только те элементы множества А, которые не принадлежат множеству В. Дополнение множества В до множества А обозначают В'А

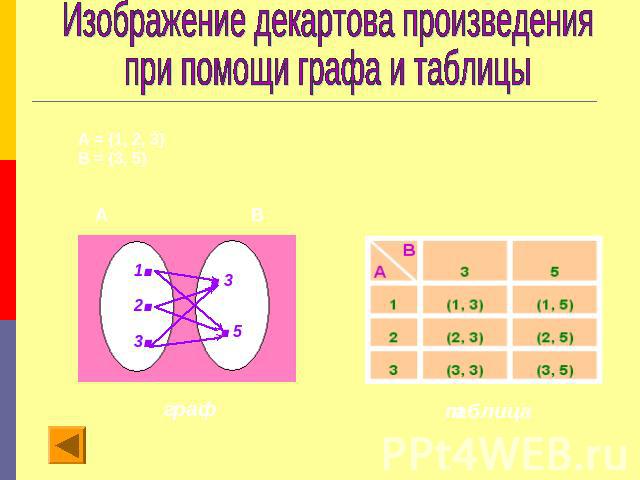
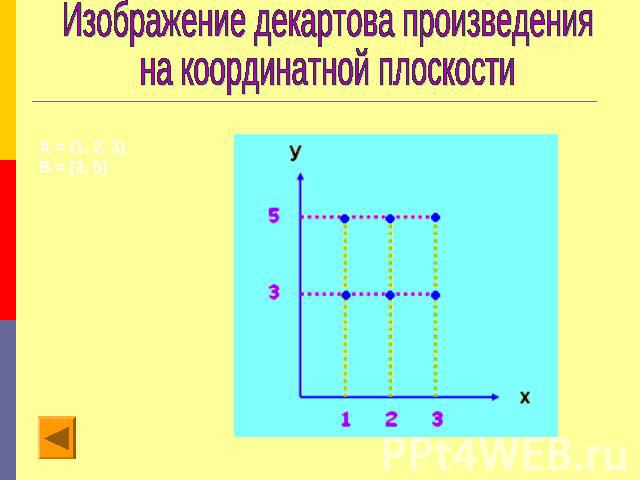
Декартово произведение множествДекартовым произведением множеств А и В называется множество всех пар, первая компонента которых принадлежит множеству А, а вторая компонента принадлежит множеству В. Декартово произведение обозначают А X В.Если множества А и В конечны и содержат небольшое число элементов, можно изобразить декартово произведение этих множеств при помощи графа или таблицы.Декартово произведение двух числовых множеств (конечных и бесконечных) можно изображать на координатной плоскости.Операцию нахождения декартова произведения множеств называют декартовым умножением.

Изображение декартова произведения при помощи графа и таблицы

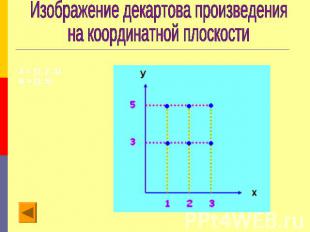
Изображение декартова произведения на координатной плоскости