Презентация на тему: Множества и операции над ними

Георг Кантор (1845 – 1918) «Множество – единое имя для совокупности всех объектов, обладающих данным свойством»

a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, что …» - знак принадлежности, a А - знак включённости, A B «Множество – единое имя для совокупности всех объектов, обладающих данным свойством»

Множество Словесное описание Поэлементное описание Перечисление элементов Цифры десятичной системы счисления Множество состоит из цифр 0,1,2,3,4,5,6,7,8,9 {0,1,2,3,4,5,6,7,8,9} Гласные буквы латинского алфавита Множество состоит из букв А,Е,Ё,И,О,У,Ы,Э,Ю,Я {А,Е,Ё,И,О,У,Ы,Э,Ю,Я}

Способы задания множеств Множество Словесное описание множества {10,15,20,…,90,95} Множество всех двузначных чисел, кратных 5 {1,4,9,16,25,36,…} Множество всех квадратов натуральных чисел N Множество натуральных чисел Q Множество рациональных чисел {х|2

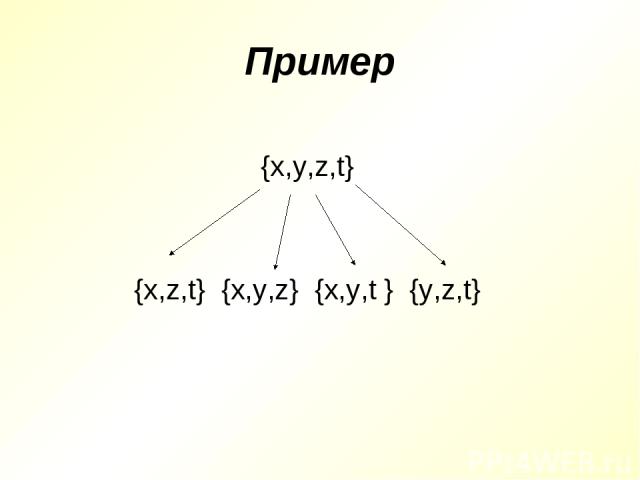
Подмножество Элементы, образующие множество А, можно объединять не сразу все вместе, а группируя их в разных комбинациях. Если каждый элемент множества В является элементом множества А, то множество В называют подмножеством множества А. Обозначение: В ϲ А

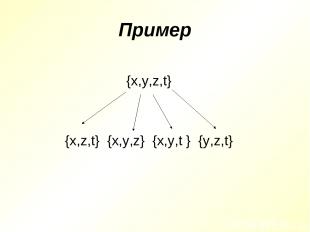
Пример {x,y,z,t} {x,z,t} {x,y,z} {x,y,t } {y,z,t}

a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества - знак принадлежности, a А - знак включённости, A B { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, что …» Леонард Эйлер (1707 – 1783) А В «Множество – единое имя для совокупности всех объектов, обладающих данным свойством»

Х Y и Х={1;3;5;7;9} Y={3;6;9;12;15} Х Y = ? Х Y = {3;9} 1 3 5 7 9 3 6 9 12 15 А В a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества - знак принадлежности, a А - знак включённости, A B { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, что …» «Множество – единое имя для совокупности всех объектов, обладающих данным свойством» и Пересечением множеств А и В называют множество, состоящее из всех общих элементов множеств А и В

a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества - знак принадлежности, a А - знак включённости, A B { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, что …» и Пустым множеством называется множество, не содержащее ни одного элемента М = {1;4;9;…} N = {2;3} М N = ? М N = 1 4 9 2 3 «Множество – единое имя для совокупности всех объектов, обладающих данным свойством» Пустое множество М N 16 …

В Пустое множество А или Х={1;3;5;7;9} Y={3;6;9;12;15} Х Y = ? Х Y = {1;3;5;7;9;6;12;15} Х Y 3 9 1 3 5 7 9 6 6 12 15 12 15 a, b, …, x, y, z – элементы множества A, B, … X, Y, Z - множества - знак принадлежности, a А - знак включённости, A B { ; } – используется для перечисления элементов | - заменяет словосочетание «…таких, что …» и «Множество – единое имя для совокупности всех объектов, обладающих данным свойством» Объединением множеств А и В называют множество, состоящее из всех элементов, которые принадлежат хотя бы одному из этих множеств – или множеству А или множеству В или