Презентация на тему: Золотое сечение

Золотое сечение ГОУ СПО «Прокопьевский транспортный техникум» г. Прокопьевск, 2015 Учитель: Гилева В.Г.

«...Геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе - с драгоценным камнем...». Иоганн Кеплер

Деление отрезка в золотом отношении Дано: отрезок АВ. Построить: золотое сечение отрезка АВ, т.е. точку Е так, чтобы . Построение. Построим прямоугольный треугольник, у которого один катет в два раза больше другого. Для этого восстановим в точке В перпендикуляр к прямой АВ и на нем отложим отрезок ВС= . Далее, соединим точки А и С, отложим отрезок CD=CB, и наконец AE=AD. Точка Е является искомой, она производит золотое сечение отрезка АВ.

Золотой треугольник А В С Золотым называется такой равнобедренный треугольник, основание и боковая сторона которого находятся в золотом отношении:
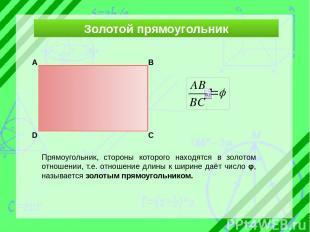
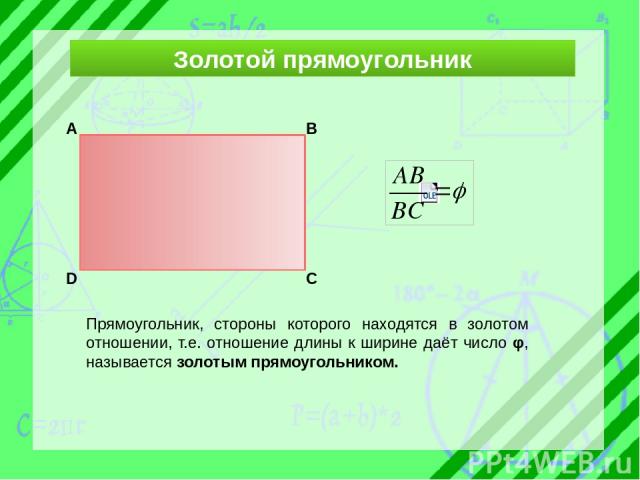
Золотой прямоугольник Прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число φ, называется золотым прямоугольником. А В С D

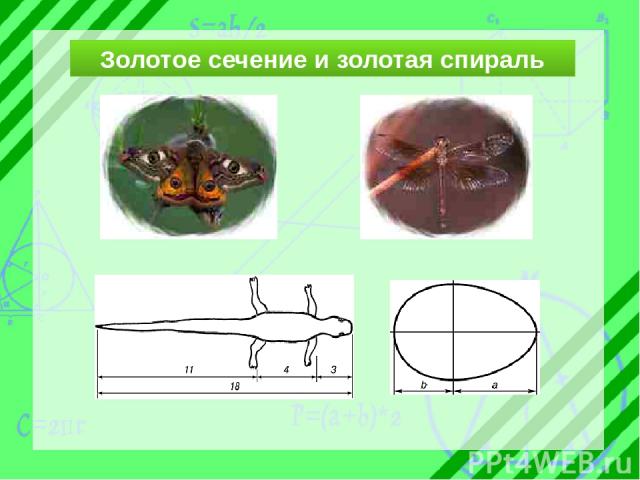
Золотое сечение и золотая спираль

Золотое сечение и золотая спираль
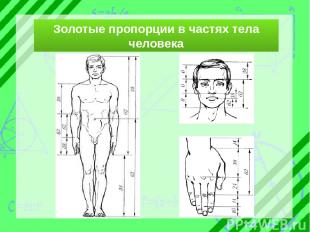
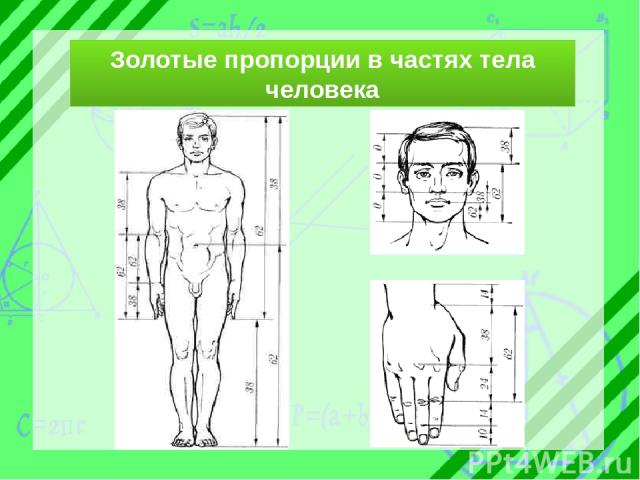
Золотые пропорции в частях тела человека
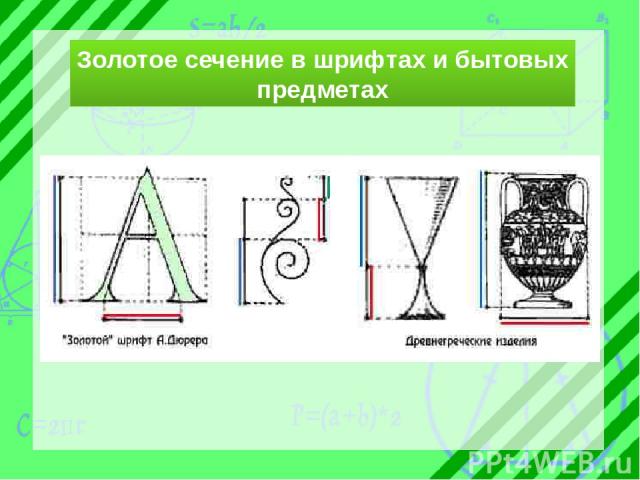
Золотое сечение в шрифтах и бытовых предметах

Домашнее задание Задача 1. Начни с золотого прямоугольника. Отрежь от него квадрат – и ты получишь маленький, но по прежнему золотой прямоугольник. А теперь попробуй отрезать другой квадрат! Сделай вывод. Задача 2. Древнегреческие математики не имели микрокалькуляторов для облегчения своих исследований. Вместо этого им приходилось полагаться на точность построений с помощью циркуля. Тем не менее они сумели открыть чудесные свойства золотого прямоугольника 1×1,618. Одно из открытий касалось прямоугольника 0,618 × 1. Является ли этот прямоугольник золотым? Во сколько раз его площадь меньше площади прямоугольника 1 × 1,618?

Плитки Пенроуза В античной науке была широко известна «проблема паркета», которая сводится к плотному заполнению плоскости геометрическими фигурами одного вида. Как известно, такое заполнение может быть осуществлено с помощью треугольников, квадратов и шестиугольников. С помощью пятиугольников (пентагонов) такое заполнение невозможно.

Проблема паркета Рассмотрим еще раз внимательно правильный пятиугольник, называемый также пентагоном или пентаграммой, плоскую геометрическую фигуру, основанную на «золотом сечении». Правильный пятиугольник или пентагон Как известно, после проведения в пентагоне диагоналей исходный пентагон может быть представлен как совокупность трех типов геометрических фигур. В центре находится новый пентагон, образуемый точками пересечения диагоналей. Остальная часть пентагона включает в себя пять равнобедренных треугольников, окрашенных в желтый цвет, и пять равнобедренных треугольников, окрашенных в красный цвет. Желтые треугольники являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют острые углы в 36° при вершине и острые углы в 72° при основании. Красные треугольники также являются «золотыми», так как отношение бедра к основанию равно золотой пропорции; они имеют тупой угол в 108° при вершине и острые углы в 36° при основании. А теперь соединим два желтых треугольника и два красных треугольника их основаниями. В результате мы получим два «золотых» ромба. Первый из них (желтый) имеет острый угол в 36° и тупой угол в 144°. Левый ромб будем называть тонким ромбом, а правый ромб – толстым ромбом. Золотые ромбы

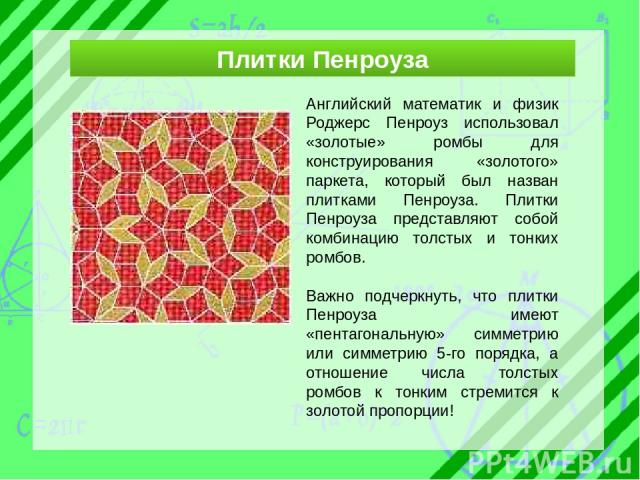
Английский математик и физик Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета, который был назван плитками Пенроуза. Плитки Пенроуза представляют собой комбинацию толстых и тонких ромбов. Важно подчеркнуть, что плитки Пенроуза имеют «пентагональную» симметрию или симметрию 5-го порядка, а отношение числа толстых ромбов к тонким стремится к золотой пропорции! Плитки Пенроуза

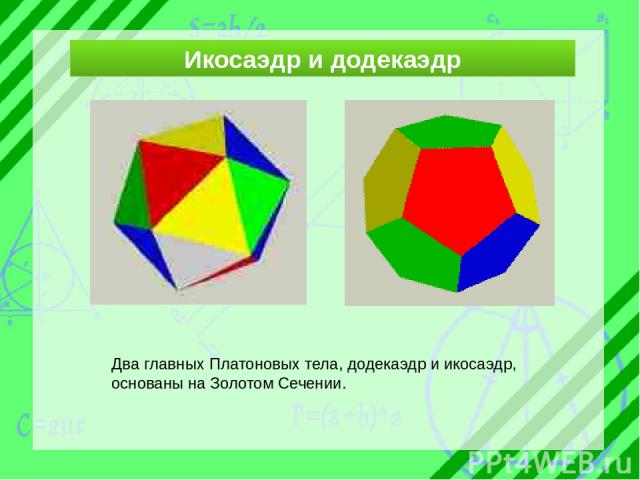
Икосаэдр и додекаэдр Два главных Платоновых тела, додекаэдр и икосаэдр, основаны на Золотом Сечении.

Золотое сечение в изобразительном искусстве

Золотое сечение и золотая спираль в живой природе

Пирамида золотого сечения

Пирамида золотого сечения