Презентация на тему: Матрицы

Матрицы

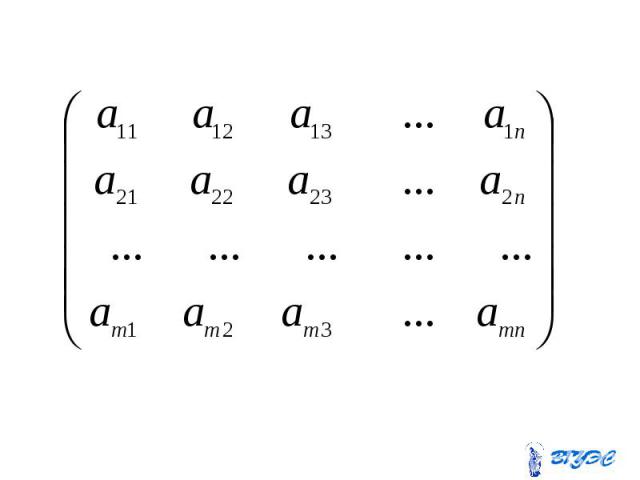
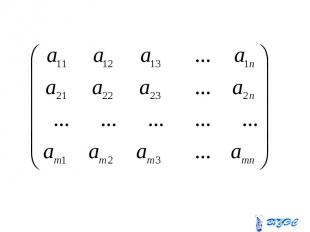
Матрицей называется прямоугольная таблица чисел . Если матрица содержит строк и столбцов, то говорят, что матрица имеет размерность . - порядок матрицы

Обозначение матриц Обозначение матриц

Матрица размера m m называется Матрица размера m m называется квадратной. Матрица , имеющая только одну строку называется матрицей-строкой. Матрица, имеющая только один столбец называется матрицей-столбцом .

Две матрицы считаются равными, Две матрицы считаются равными, если равны их размеры и равны элементы, стоящие на одинаковых местах. Квадратная матрица называется невырожденной (неособенной), если её определитель отличен от нуля, и вырожденной (особенной) , если определитель её равен нулю.

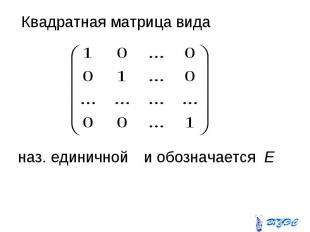
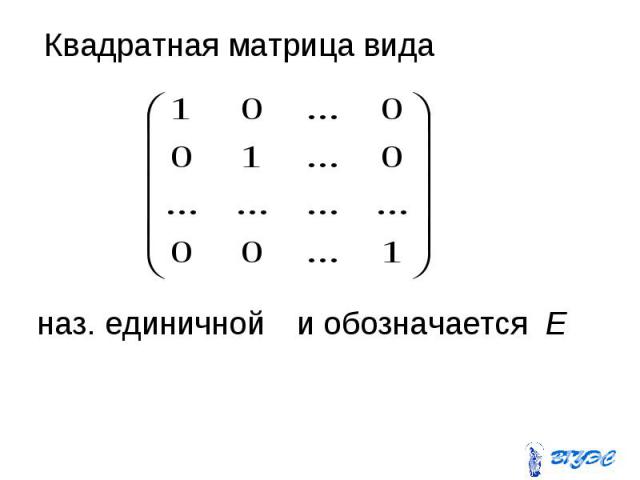
Квадратная матрица вида Квадратная матрица вида наз. единичной и обозначается Е

Матрица, все элементы которой равны нулю, наз. нулевой. Матрица, все элементы которой равны нулю, наз. нулевой. Определитель, составленный из элементов квадратной матрицы, наз. определителем матрицы. Очевидно

Матрица Матрица наз. транспонированной по отношению к матрице

Действия над матрицами. Суммой двух матриц одинаковой размерности А и В называется матрица С той же размерности, элементы которой равны суммам элементов матриц A и B с одинаковыми индексами.

Произведением матрицы на число называется матрица , получающаяся из матрицы A умножением всех её элементов на .

Разностью двух матриц А и В одинаковой размерности называется матрица С=A+(-B).

Произведением матрицы Произведением матрицы размера на матрицу размера называется матрица размера , элемент которой , стоящий в i-ой строке и j-ом столбце, равен сумме произведений элементов i-ой строки матрицы A и соответствующих элементов j-го столбца матрицы B.

Свойства операций над матрицами 1.A+B=B+A 2.(A+B)+C=A+(B+C) 3.(A+B)k=kA+kB

4. (AB)C=A(BC) 5. A(B+C)=AB+AC 6. A+O=A 7. AE=EA=A

Если и две квадратные матрицы одного порядка, то Если и две квадратные матрицы одного порядка, то

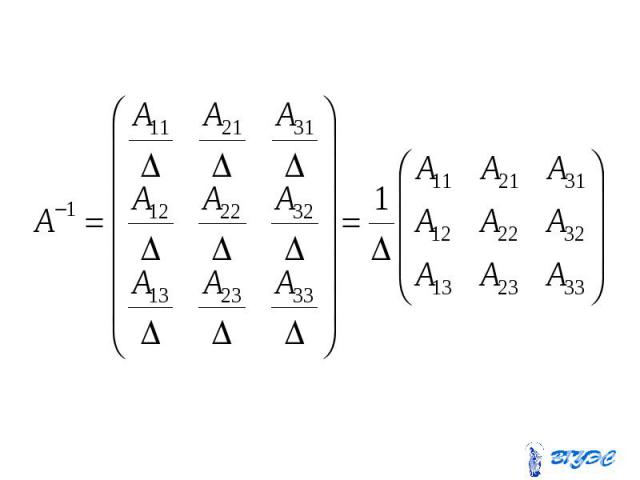
Обратная матрица Обратная матрица

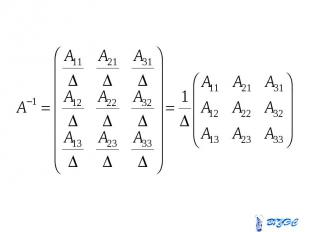
Пусть - квадратная матрица. Пусть - квадратная матрица. Обратной для неё матрицей наз. квадратная матрица того же порядка, обозначаемая и удовлетворяющая условию

Для того, чтобы квадратная матрица Для того, чтобы квадратная матрица имела обратную матрицу, необходимо и достаточно, чтобы матрица была невырожденной.

Р а н г м а т р и ц ы Рангом матрицы называется наивысший из порядков отличных от нуля миноров матрицы. Ранг матрицы A обозначается: или .

Теорема о ранге матрицы Ранг матрицы равен максимальному числу линейно – независимых строк матрицы.

Элементарные преобразования матрицы. 1.Умножение всех элементов строк на одно и то же число не равное 0. 2. Перестановка строк местами. 3. Прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и тоже число.

4.Отбрасывание одной из двух одинаковых строк. 5.Отбрасывание нулевой строки

Теорема: Элементарные преобразования не меняют ранг матрицы. Матрицы, полученные с помощью элементарных преобразований наз. эквивалентными (~).