Презентация на тему: Матрицы

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" НАШ ПРИНЦИП – КАЧЕСТВО! МАТЕМАТИКА 5informatika.net ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" СЛАЙД-ЛЕКЦИЯ № 1 ТЕМА ЛЕКЦИИ: «МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ» ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПЛАН ЛЕКЦИИ 1. ПОНЯТИЕ И ВИДЫ МАТРИЦ 2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦ 3. ОПЕРАЦИИ НАД МАТРИЦАМИ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПОНЯТИЕ И ВИДЫ МАТРИЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ОПРЕДЕЛЕНИЯ МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМО-УГОЛЬНАЯ ИЛИ КВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ. ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ ЭЛЕМЕНТАМИ МАТРИЦЫ. ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ВИДЫ МАТРИЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ И РАЗМЕР МАТРИЦЫ ООО "РЕЗОЛЬВЕНТА"

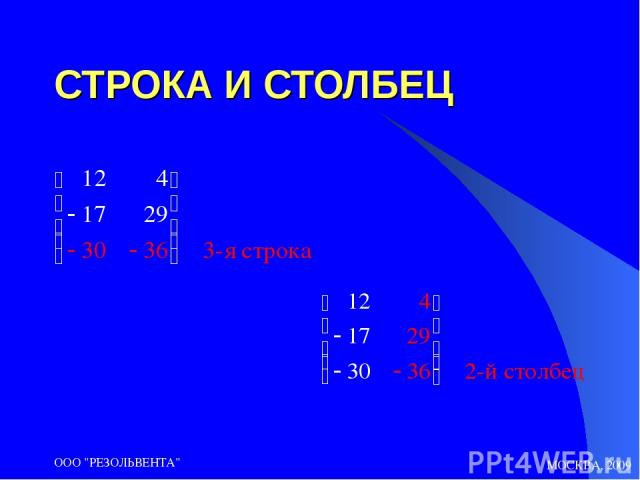
МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ СТРОКИ НУМЕРУЮТСЯ СВЕРХУ ВНИЗ, НАЧИНАЯ С № 1. СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА НАПРАВО, НАЧИНАЯ С № 1. ООО "РЕЗОЛЬВЕНТА"

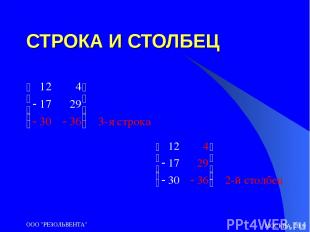
МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" СТРОКА И СТОЛБЕЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" РАЗМЕР МАТРИЦЫ МАТРИЦА, ИМЕЮЩАЯ m СТРОК И n СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ РАЗМЕРА m НА n. ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ЭЛЕМЕНТ МАТРИЦЫ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ТРЕУГОЛЬНЫЕ МАТРИЦЫ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ОПЕРАЦИИ НАД МАТРИЦАМИ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ТРАНСПОНИРОВАНИЕ МАТРИЦЫ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ) ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ВОЗМОЖНОСТЬ УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ МАТРИЦУ A, ЗАПИСАННУЮ СЛЕВА, МОЖНО УМНОЖИТЬ НА МАТРИЦУ B, ЗАПИСАННУЮ СПРАВА, ТОГДА И ТОЛЬКО ТОГДА, КОГДА ЧИСЛО СТОЛБЦОВ МАТРИЦЫ A РАВНО ЧИСЛУ СТРОК МАТРИЦЫ B ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПРАВИЛО УМНОЖЕНИЯ МАТРИЦЫ НА МАТРИЦУ КАЖДАЯ СТРОКА ЛЕВОЙ МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА КАЖДЫЙ СТОЛБЕЦ ПРАВОЙ МАТРИЦЫ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ПРИМЕР УМНОЖЕНИЯ МАТРИЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" ВАЖНЫЕ ТИПЫ КВАДРАТНЫХ МАТРИЦ ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A ООО "РЕЗОЛЬВЕНТА"

МОСКВА, 2009 ООО "РЕЗОЛЬВЕНТА" БЛАГОДАРИМ ЗА ВНИМАНИЕ! ООО "РЕЗОЛЬВЕНТА"