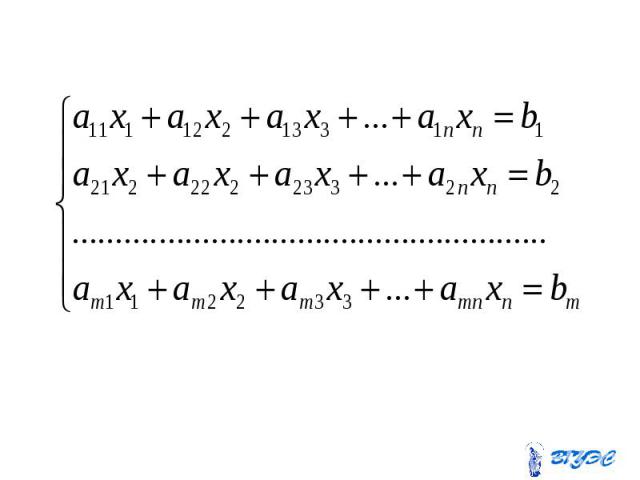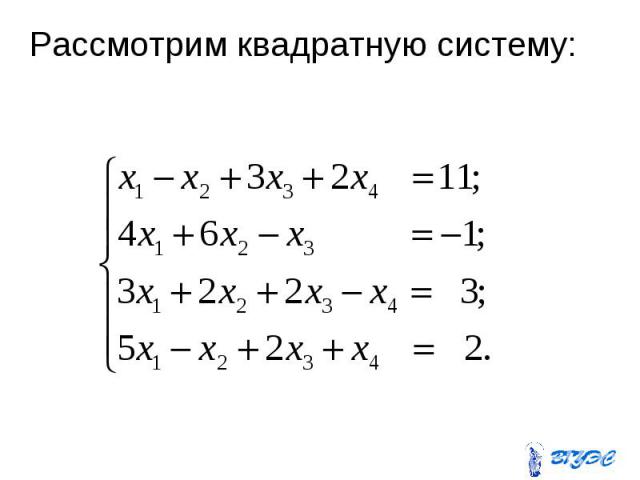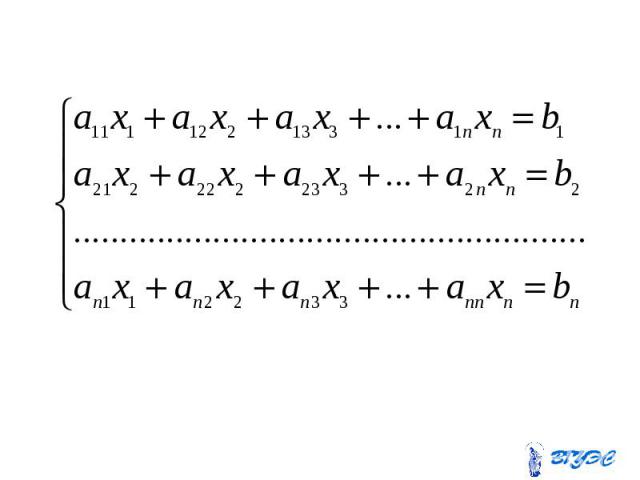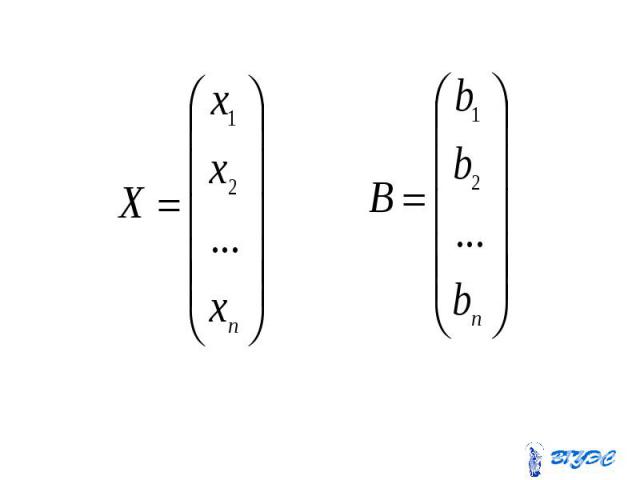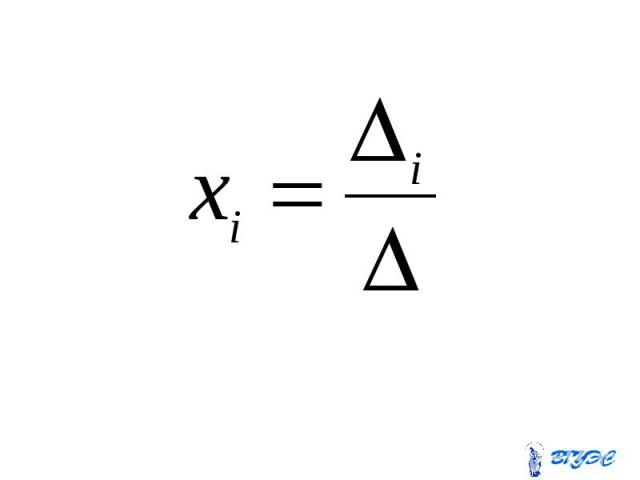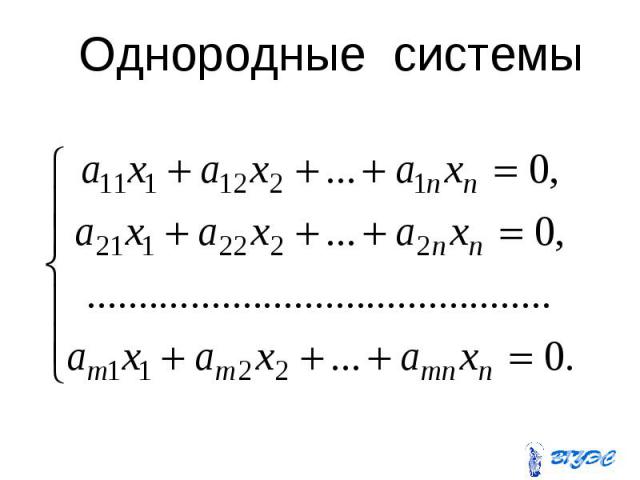Презентация на тему: Системы линейных алгебраических уравнений (СЛАУ)

Системы линейных алгебраических уравнений (СЛАУ)

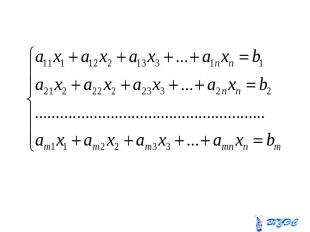
Здесь - неизвестные; Здесь - неизвестные; - коэффициенты при неизвестных, где - номер уравнения, - номер неизвестного; - свободные члены (правые части).

Система наз. неоднородной, если не все равны нулю. Система наз. неоднородной, если не все равны нулю. Система наз. однородной, если все равны нулю.

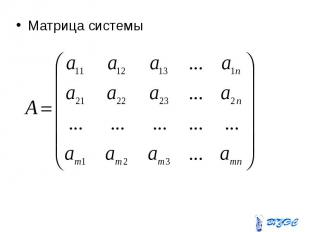
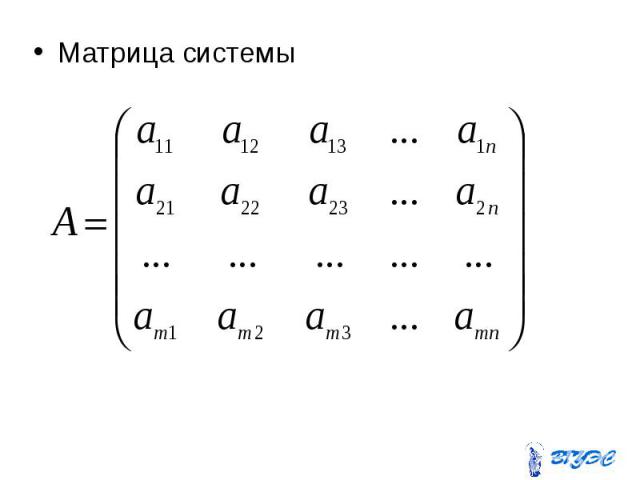
Матрица системы Матрица системы

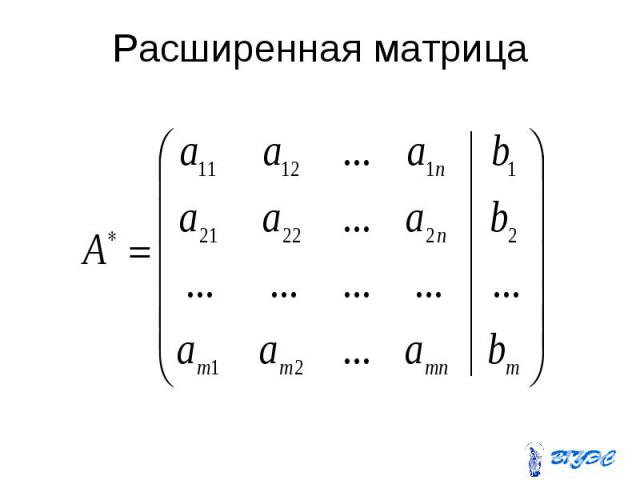
Расширенная матрица

Решением системы будем называть Решением системы будем называть упорядоченный набор чисел обращающий каждое уравнение системы в верное равенство.

Решить систему — значит найти Решить систему — значит найти все ее решения или доказать, что ни одного решения нет. Система, имеющая хотя бы одно решение, называется совместной. Если система имеет только одно решение, то она называется определенной.

Если система не имеет решений, то Если система не имеет решений, то она называется несовместной. Система, имеющая более чем одно решение, называется неопределенной (совместной и неопределенной). Если число уравнений системы совпадает с числом неизвестных , то система называется квадратной.

Две системы, множества решений Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.

Метод Гаусса

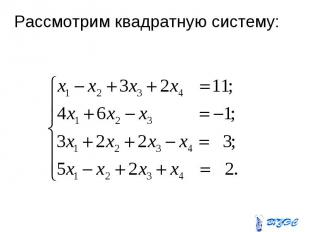
Рассмотрим квадратную систему: Рассмотрим квадратную систему:

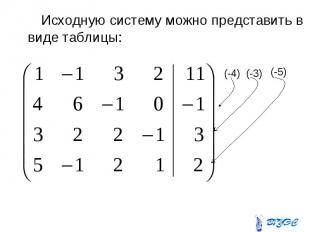
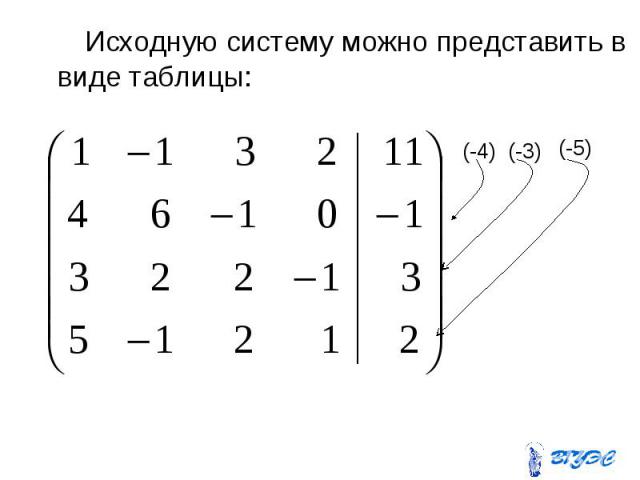
Исходную систему можно представить в виде таблицы: Исходную систему можно представить в виде таблицы:

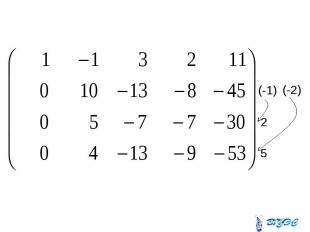
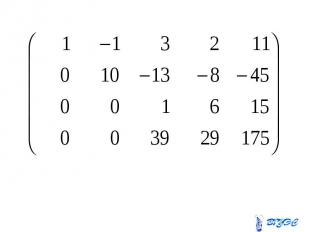
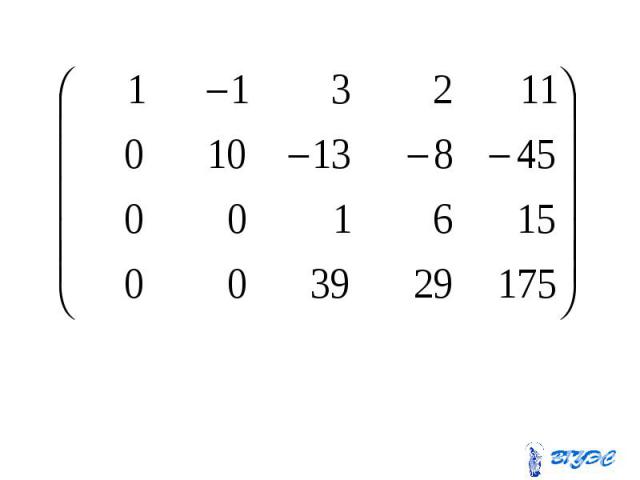
Полученная матрица соответствует системе: Полученная матрица соответствует системе:

Матричный метод

С помощью этого метода можно решать квадратные системы линейных уравнений С помощью этого метода можно решать квадратные системы линейных уравнений

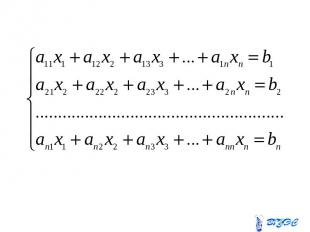
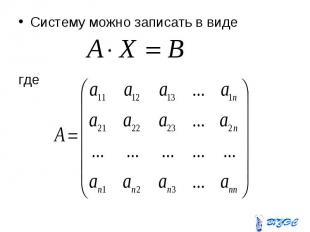
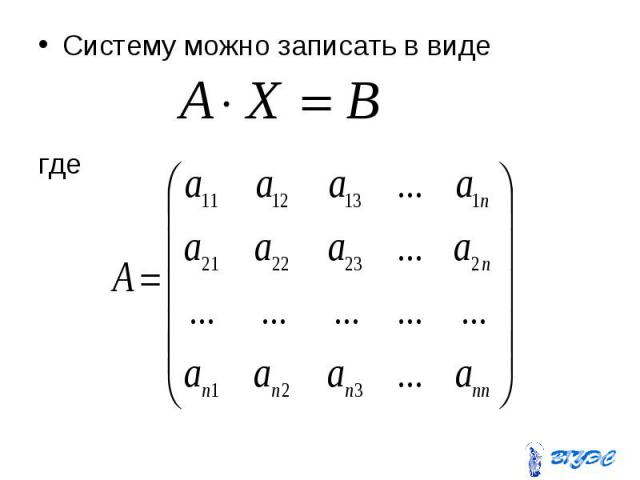
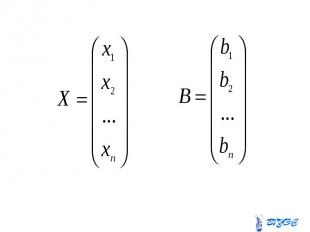
Систему можно записать в виде Систему можно записать в виде где

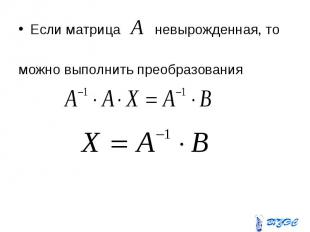
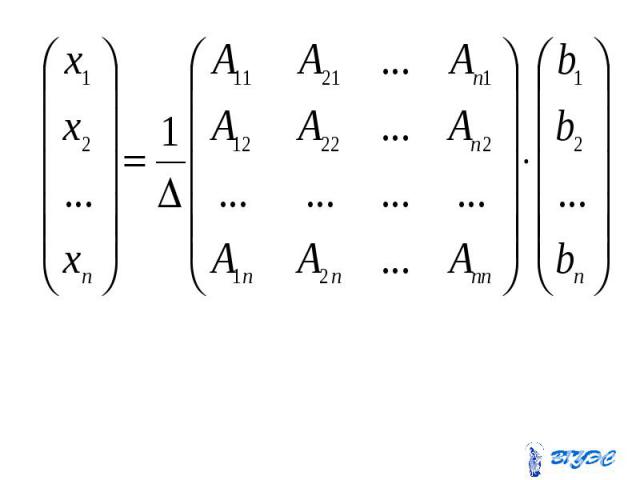
Если матрица невырожденная, то Если матрица невырожденная, то можно выполнить преобразования

Метод Крамера

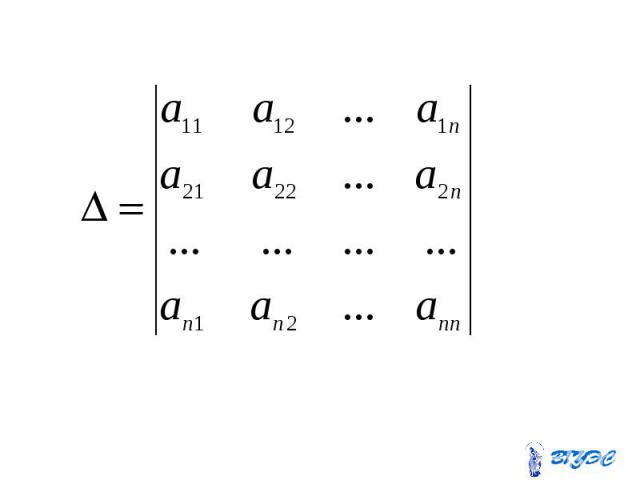
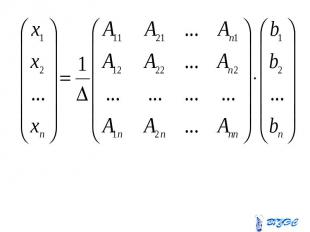
Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуле Если определитель системы линейных уравнений с неизвестными отличен от нуля, то эта система является определенной и её единственное решение находится по формуле

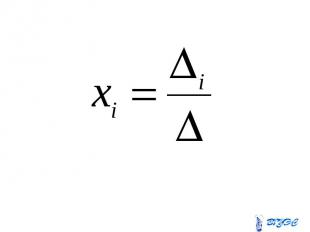
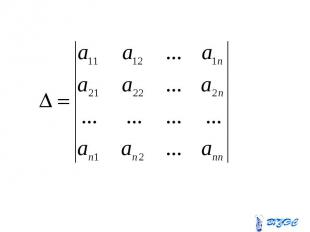
Здесь – определитель, Здесь – определитель, получающийся из определителя заменой i-го столбца столбцом свободных членов.

Если и по крайне мере один из определителей , то система не имеет решения. Если и по крайне мере один из определителей , то система не имеет решения. Если и , система либо не имеет решения, либо имеет бесконечно много решений.

Т е о р е м а К р о н е к е р а - К а п е л л и Для того чтобы система неоднородных линейных уравнений с неизвестными была совместной, необходимо и достаточно, чтобы

Замечание. Пусть система совместна и Замечание. Пусть система совместна и если число уравнений равно числу неизвестных, то система имеет единственное решение; если число уравнений меньше числа неизвестных, то система имеет множество решение.

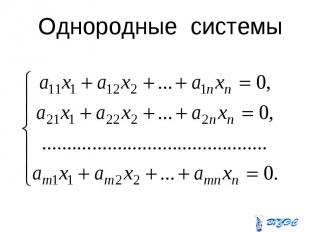
Однородные системы

Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.