Презентация на тему: Геометричиские преобразования в пространстве

Геометричиские преобразования в пространстве Сивцева Ольга. Ставрополь. 2007 год

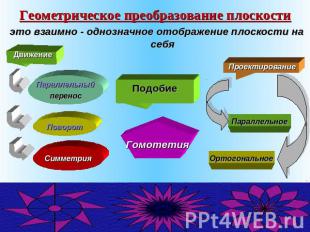
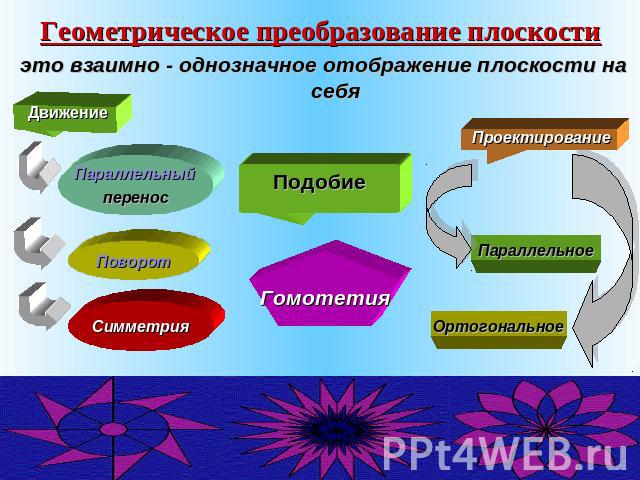
Геометрическое преобразование плоскости это взаимно - однозначное отображение плоскости на себя

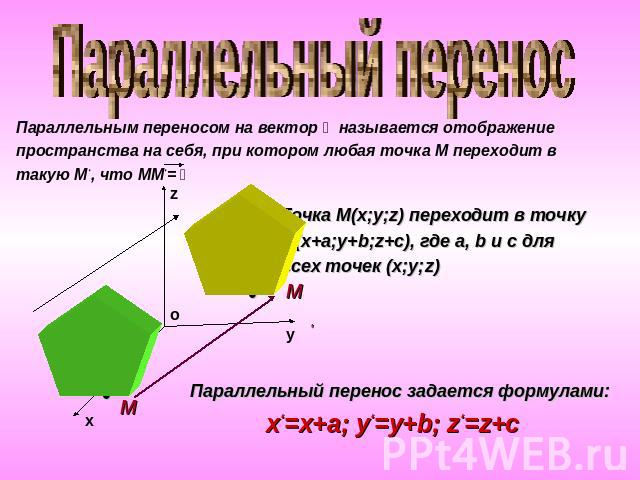
Параллельный перенос Параллельным переносом на вектор ḡ называется отображение пространства на себя, при котором любая точка М переходит в такую М‘, что ММ‘= ḡ Точка М(х;у;z) переходит в точку М(х+а;у+b;z+c), где а, b и с для всех точек (х;у;z) Параллельный перенос задается формулами: х‘=х+а; у‘=у+b; z‘=z+c

Параллельный перенос Параллельный перенос есть движение Движение, сохраняющее направление,является параллельным переносом

поворот Поворотом плоскости около данной точки называется такое движение, при котором каждый луч, исходящий из этой точки, поворачивается на один и тот же угол в одном и том же направлении – угол поворотаТочка О-центр поворота

Поворот в пространстве Спутники вращаются вокруг планет Планеты вращаются вокруг солнца

Вращение галактик в космосе

Симметрия «Симметрия является той идеей, посредством которой человек на протяжении веков пытается постичь и создать порядок, красоту и совершенство » Г.Вейль

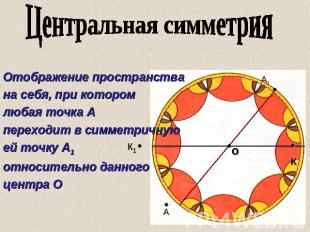
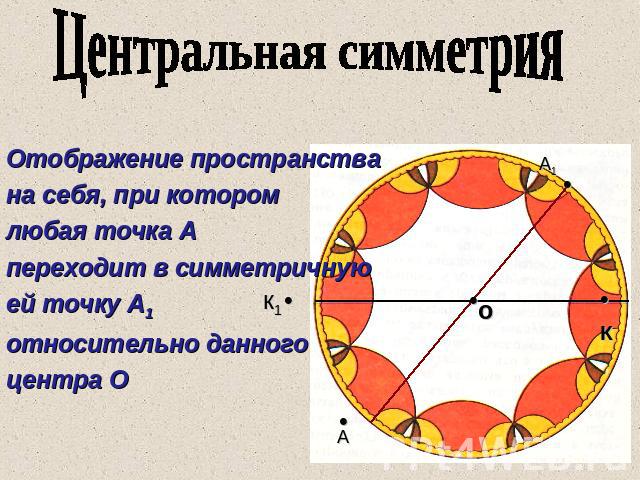
Центральная симметрия Отображение пространства на себя, при котором любая точка А переходит в симметричную ей точку А1 относительно данного центра О

Применение центральной симметрии

Центральная симметрия в природе кактусы

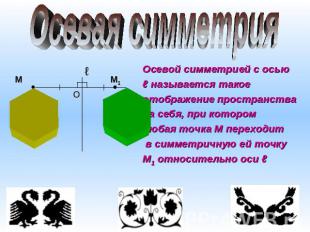
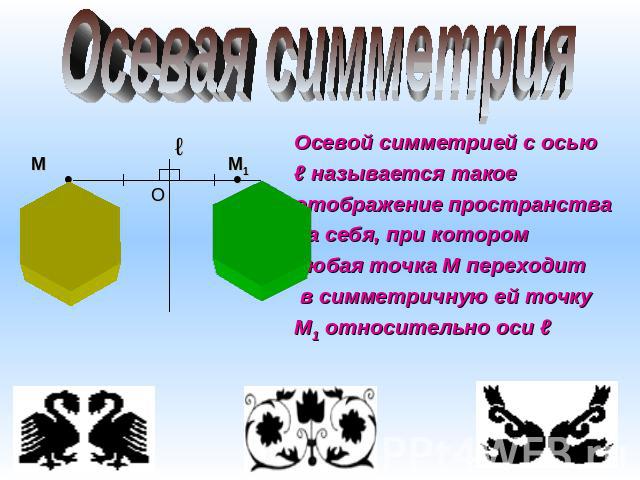
Осевая симметрия Осевой симметрией с осьюℓ называется такое отображение пространствана себя, при котором любая точка М переходит в симметричную ей точкуМ1 относительно оси ℓ

Осевая симметрия в архитектуре

Церковь Андрея Первозванного.г. Ставрополь

Осеваясимметрия животного мира

Осевая симметрия в природе

Осевая симметрия технике

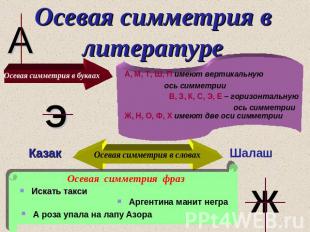
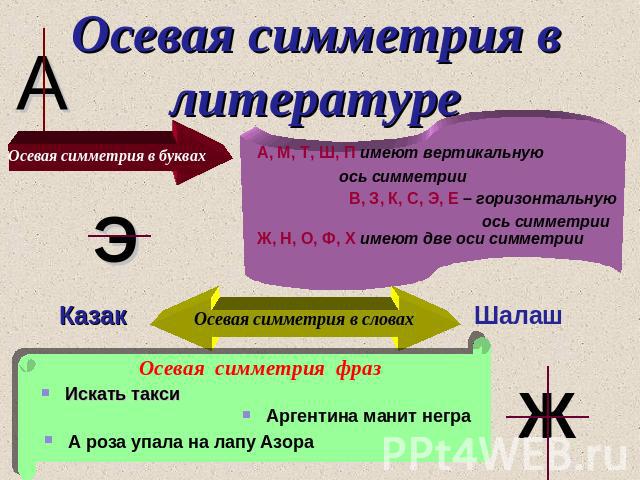
Осевая симметрия в литературе А, М, Т, Ш, П имеют вертикальную ось симметрии В, З, К, С, Э, Е – горизонтальную ось симметрии Ж, Н, О, Ф, Х имеют две оси симметрии Осевая симметрия фраз Искать такси Аргентина манит негра

Зеркальная симметрия Зеркальной симметрией(симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка Х переходит в симметричную ей относительно данной плоскости точку Х '

З е р к а л ь н а я с и м м е т р и я в П р и р о д е

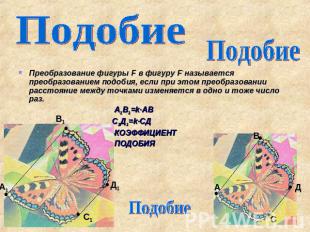
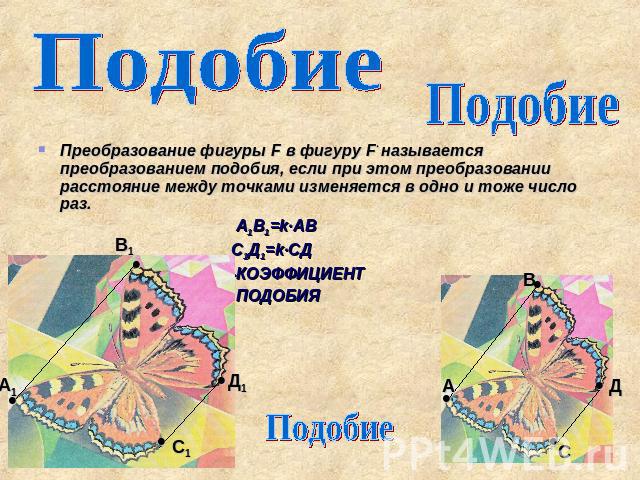
Подобие Подобие Преобразование фигуры F в фигуру F‘ называется преобразованием подобия, если при этом преобразовании расстояние между точками изменяется в одно и тоже число раз. А1В1=k∙АВ С1Д1=k∙СД k-КОЭФФИЦИЕНТ ПОДОБИЯ

Гомотетия Гомотетией с центром О и коэффициентом k≠0 называется геометрическое преобразование, которое произвольно взятую точку А переводит в такую точку А‘, что ОА‘=k∙ОА

Кино в кинотеатрах

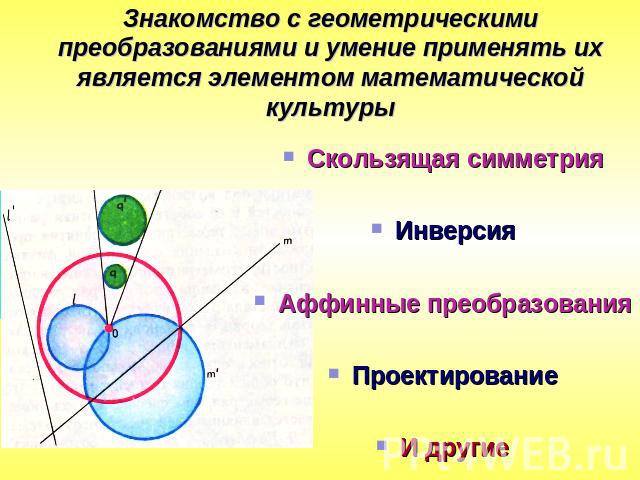
Знакомство с геометрическими преобразованиями и умение применять их является элементом математической культуры Скользящая симметрияИнверсияАффинные преобразованияПроектированиеИ другие