Презентация на тему: Сжатие(растяжение) графика вдоль оси ординат

Сжатие(растяжение) графика вдоль оси ординат

Содержание. Определение.Алгоритм построения.Зеркальное отражение графиков.Примеры.Задания.

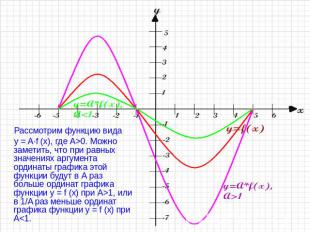
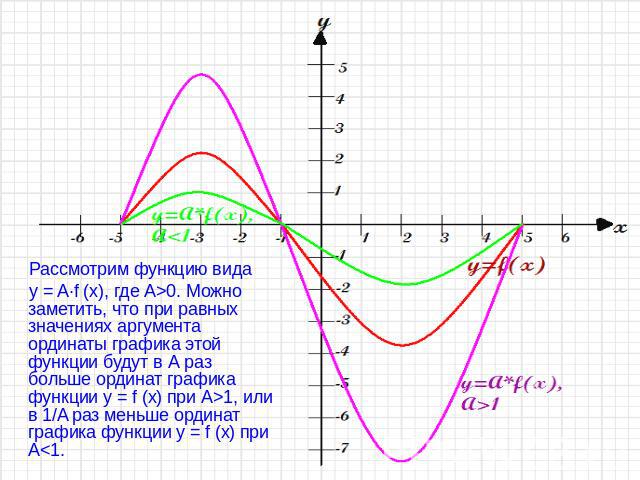
Рассмотрим функцию вида y = A∙f (x), где A>0. Можно заметить, что при равных значениях аргумента ординаты графика этой функции будут в А раз больше ординат графика функции y = f (x) при A>1, или в 1/A раз меньше ординат графика функции y = f (x) при A<1.

Для построения графика функции y = A ∙ f(x) следует: Построить график функции y = f (x)Увеличить или уменьшить его ординаты в А раз.

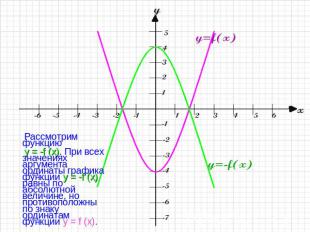
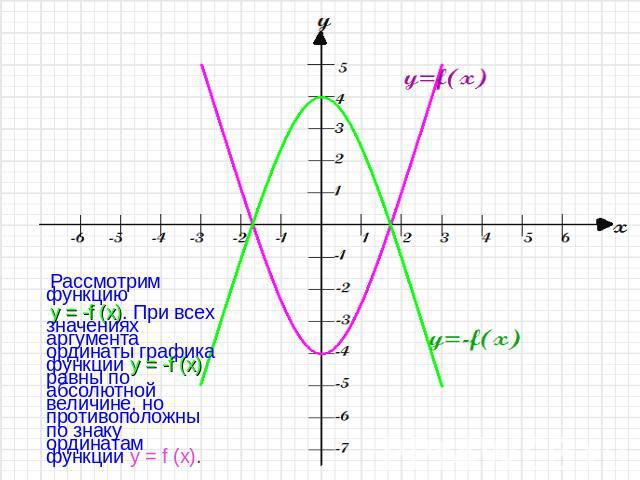
Рассмотрим функцию y = -f (x). При всех значениях аргумента ординаты графика функции y = -f (x) равны по абсолютной величине, но противоположны по знаку ординатам функции y = f (x).

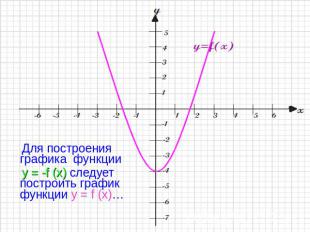
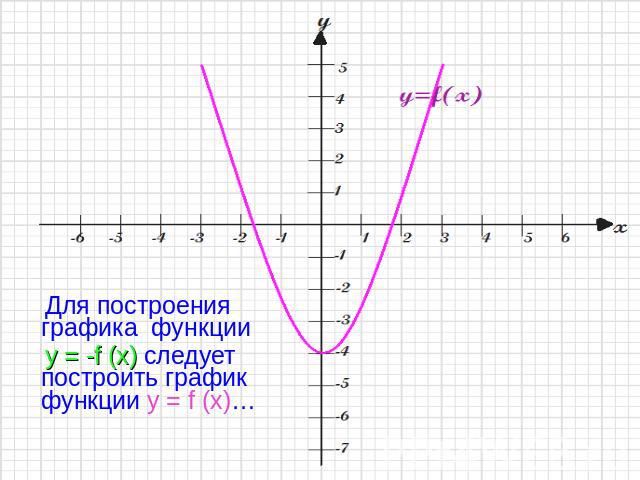
Для построения графика функции y = -f (x) следует построить график функции y = f (x)…

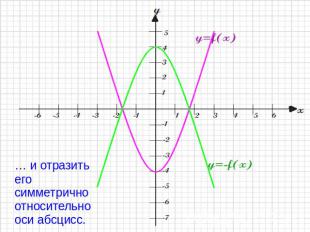
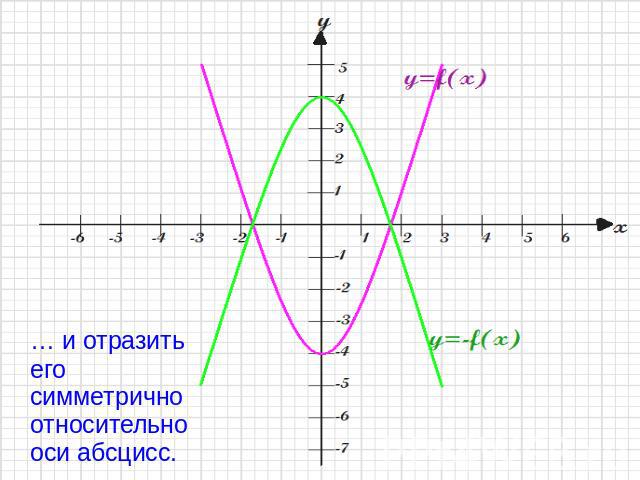
… и отразить его симметрично относительно оси абсцисс.

Соединяя знания о построении функции y = A∙f (x), где A>1 с последним правилом, мы можем построить график функции y = A∙f (x) для значения А любого знака.

Рассмотрим примеры

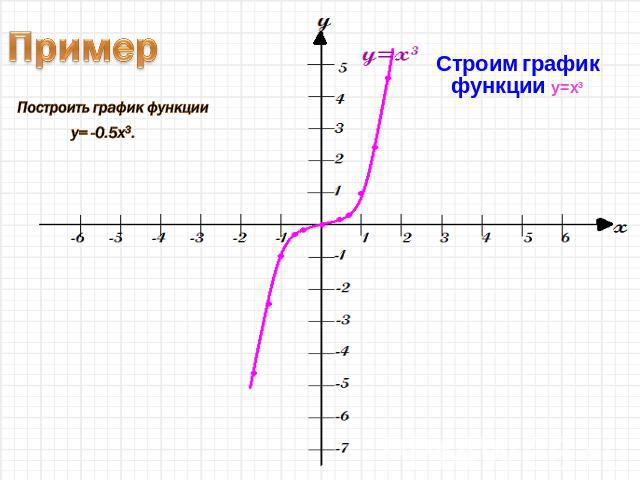
Пример 1 Построить график функции y=-0.5x3.

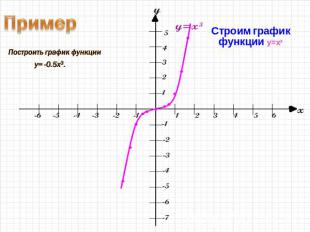
Строим график функции y=x3Строим график функции y=x3

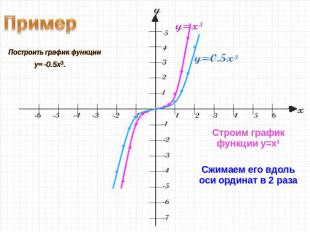
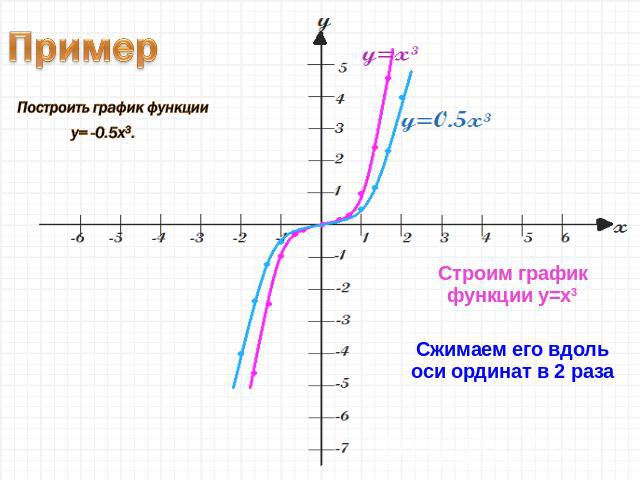
Строим график функции y=x3Сжимаем его вдоль оси ординат в 2 раза

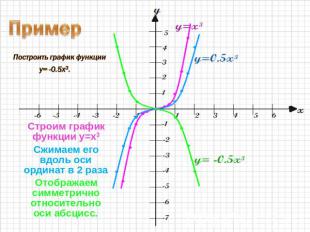
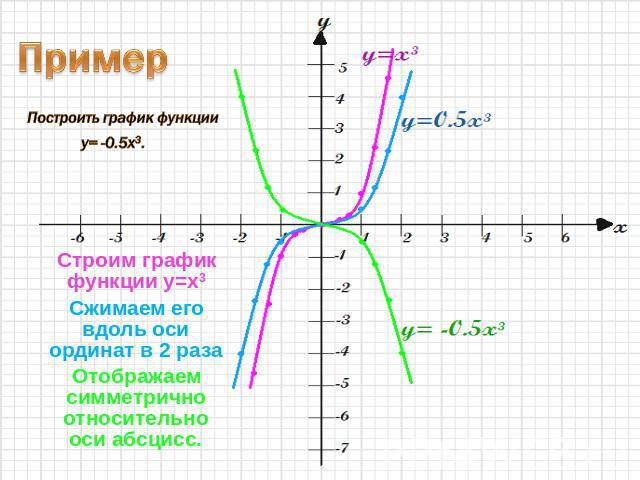
Пример Построить график функции y= -0.5x3. Строим график функции y=x3Сжимаем его вдоль оси ординат в 2 разаОтображаем симметрично относительно оси абсцисс.

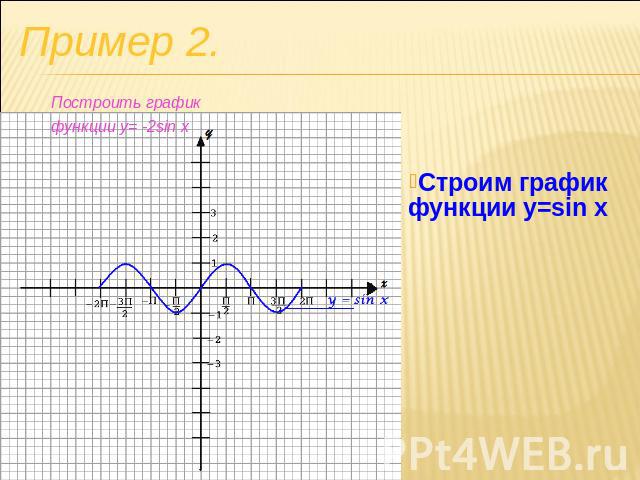
Построить график функции y= -2sin x.

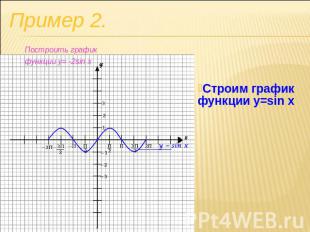
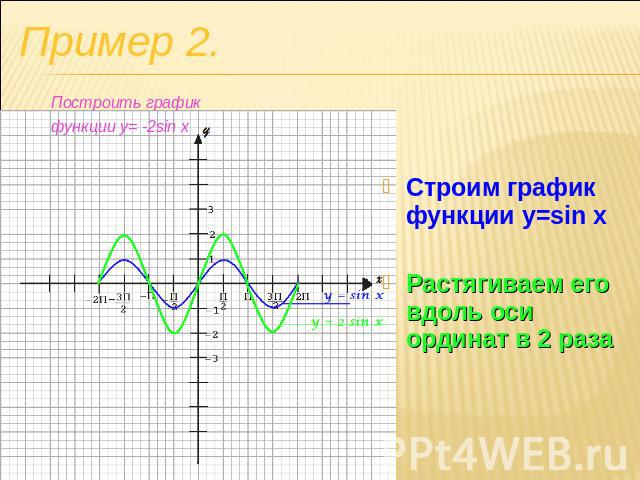
Строим график функции y=sin x Пример 2. Построить график функции y= -2sin x

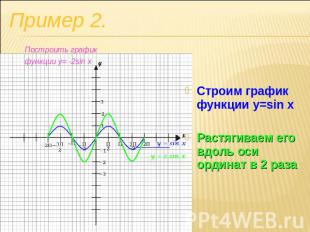
Строим график функции y=sin xРастягиваем его вдоль оси ординат в 2 раза

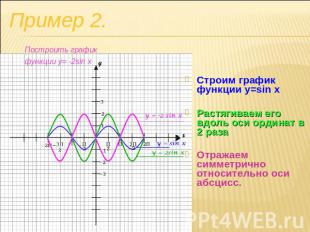
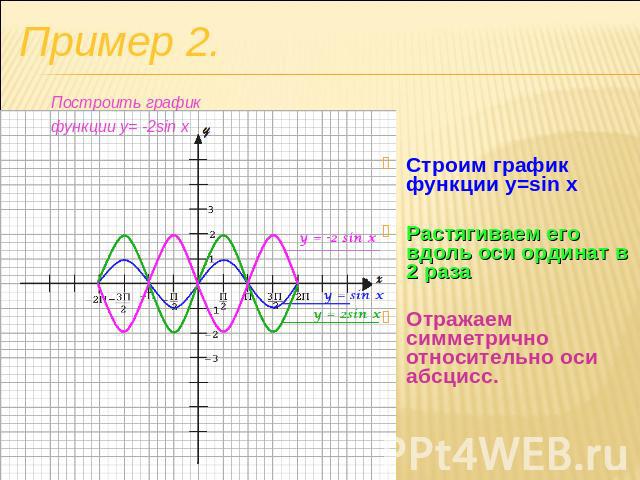
Пример 2. Построить график функции y= -2sin x Строим график функции y=sin xРастягиваем его вдоль оси ординат в 2 разаОтражаем симметрично относительно оси абсцисс.

Задания.