Презентация на тему: Средняя линия треугольника

Средняя линия треугольника Учитель: Николаева А. Ю.ГОУ СОШ № 557г. Санкт-Петербург

Каким образом эти треугольники поделили на две группы?

Отрезок, соединяющий середины двух сторон,называют СРЕДНЕЙ ЛИНИЕЙ ТРЕУГОЛЬНИКА.Задача: Найти длину АС, если MN = 4 см.AM = MB и CN = NBMN – средняя линия ABC

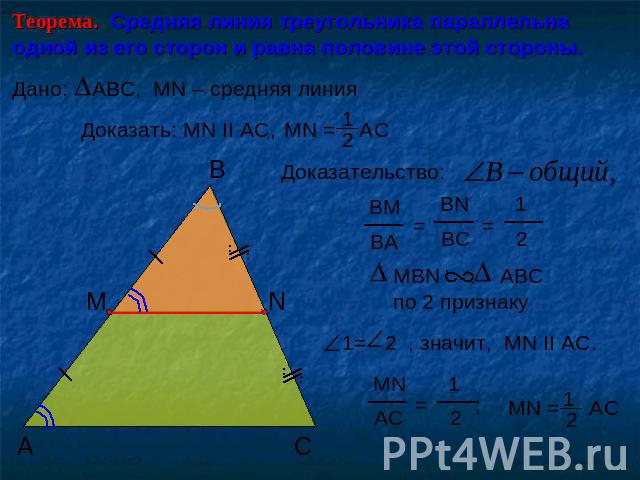
Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.Дано:ABC, МN – средняя линияДоказать: МN II АС, Доказательство: MBN ABC по 2 признаку 1= 2 , значит, МN II АС.

Найдите периметр треугольника АВС.Запомни! Периметр треугольника, вершины которого являются серединами сторон данного треугольника, равен половине его периметра.

Теорема Фалеса: если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.

Определите вид четырехугольника, который получится от последовательного соединения середин сторон любого выпуклого четырехугольника.PQ – средняя линия ABDEF – средняя линия BDCPQFE – параллелограмм ( по I признаку )

Вариньон Пьер(1654–22.XII 1722) Французский математик и механик, член Французской АН (с 1688). Родился в Каенне. Изучал философию и математику. С 1688 – профессор математики в Коллеже Мазарини, с 1704 – в Коллеж де Франс.Основные работы относятся к геометрии и статике. Исходя из теории сложных движений сформулировал (ок. 1710) закон параллелограмма сил. Развил понятие момента сил и предложил геометрическое доказательство теоремы о том, что момент равнодействующей двух сходящихся сил равен сумме моментов составляющих сил (теорема Вариньона). Его трактат “Новая механика, или статика”, проект которого был опубликован в 1686, был издан посмертно в 1725. Установил (1687) теорему о скользящих векторах для случая сходящейся системы сил. Одним из первых начал пользоваться математическим анализом. Изучал равновесие и движение жидкости. Дал объяснение закона Торричелли. Полагая, что вес колонны воды пропорционален высоте h, нашел выражение для закона Торричелли

Итог урока Какие новые знания получены на уроке?Что называют средней линией треугольника?Сформулируйте теорему о средней линии треугольника.

Домашнеезадание:П. 62, вопрос 8Задачи № 566, 568 (а) Дополнительная задача: В прямоугольном треугольнике АВС < C = 900, < A = 300,СВ = 6 см. Найти периметр треугольника, вершины которого являются серединами сторон данного треугольника.