Презентация на тему: Шар, вписанный в пирамиду, призму, конус

Потенциал исследовательской деятельности в осуществлении профильного обучения  Подготовлено Г.И. Винокуровойг. Елец, МОУ Лицей № 24

Цели и задачи метода исследовательской деятельности в профильном обучении по математике Цель обучения - развитие творческой, самостоятельной и свободной личности, стремящейся к самореализации, саморазвитию и достижению успехов в учебе.Задача состоит в поиске новых путей совершенствования учебного процесса в школе, которые предполагают использование всего спектра образовательных возможностей, предусматривающих инновационные формы, методы и средства, направленные на развитие индивидуальных и личностных качеств учащихся. Одним из методов – исследовательская деятельность учащихся для получения дополнительных знаний при решении нестандартных задач.

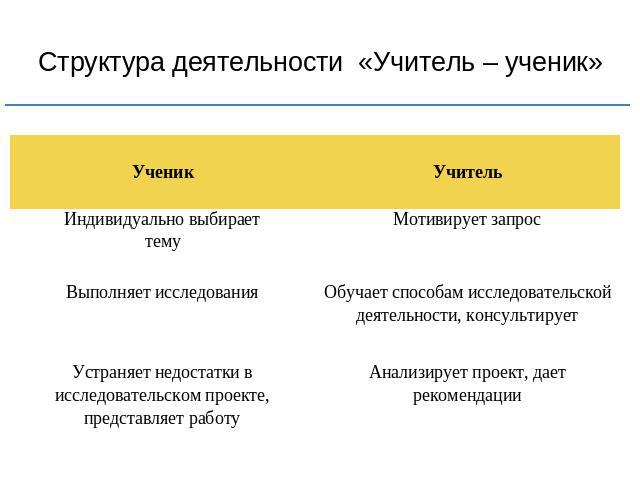
Структура деятельности «Учитель – ученик»

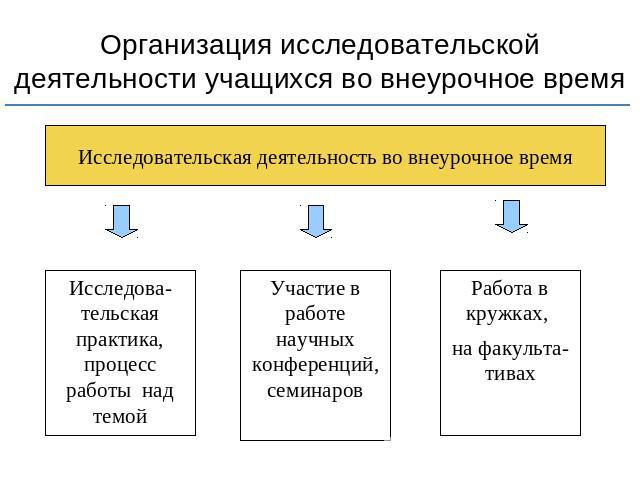
Организация исследовательской деятельности учащихся во внеурочное время

Организация творческой исследовательской деятельности учащихся Самостоятельная работа включает воспроизводящие и творческие процессы в деятельности школьников. Три уровня самостоятельной деятельности:репродуктивный (тренировочный);реконструктивный;творческий (поисковый).

Этапы подготовки исследовательской работы Руководителем исследовательской работы является учитель. Деятельность учителя заключается в следующем: предложение и корректировка темы работы школьника;обсуждение содержания и плана данной работы;рекомендации по подбору литературы;планирование и контроль за выполнением работы;написание рецензии, содержащей анализ работы и еёоценку.

Тема: «Шар, вписанный в пирамиду, призму, конус» Подготовила: ученица 11 «А» класса Дёмина ЕвангелинаПедагог-консультант: Винокурова Г. И., учитель математики

Цели и задачи: Цели:усвоение теоретического материала;рассмотрение задач на данную тему и совершенствование навыков их решения;формирование грамотности при систематизации знаний по данной теме Задачи:научиться применять полученные знания на практике;улучшить навыки работы с компьютерными технологиями;выработать навыки критического мышления

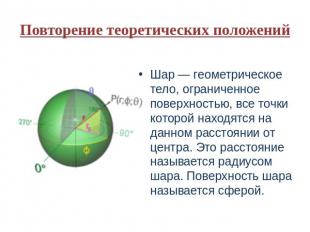
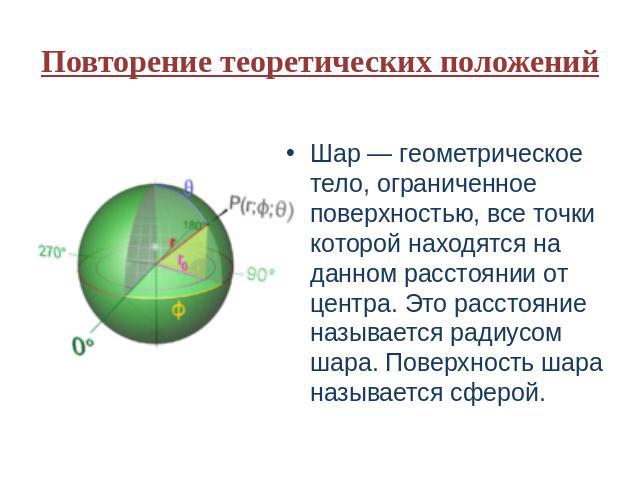
Повторение теоретических положений Шар — геометрическое тело, ограниченное поверхностью, все точки которой находятся на данном расстоянии от центра. Это расстояние называется радиусом шара. Поверхность шара называется сферой.

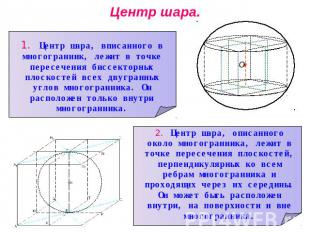
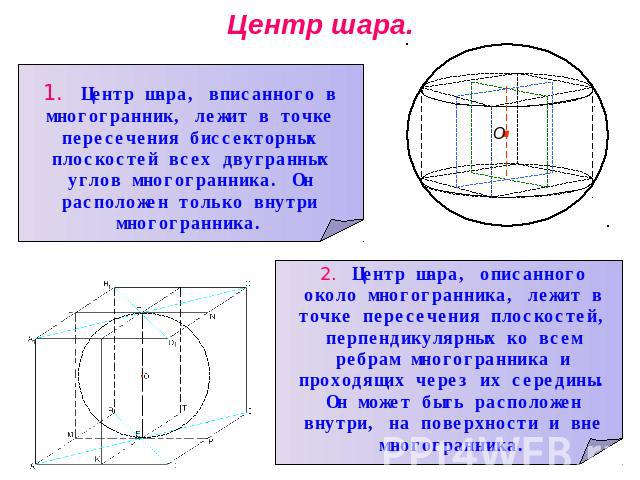
Центр шара. 1. Центр шара, вписанного в многогранник, лежит в точке пересечения биссекторных плоскостей всех двугранных углов многогранника. Он расположен только внутри многогранника.2. Центр шара, описанного около многогранника, лежит в точке пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины. Он может быть расположен внутри, на поверхности и вне многогранника.

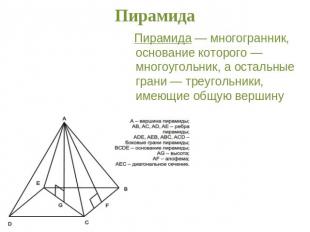
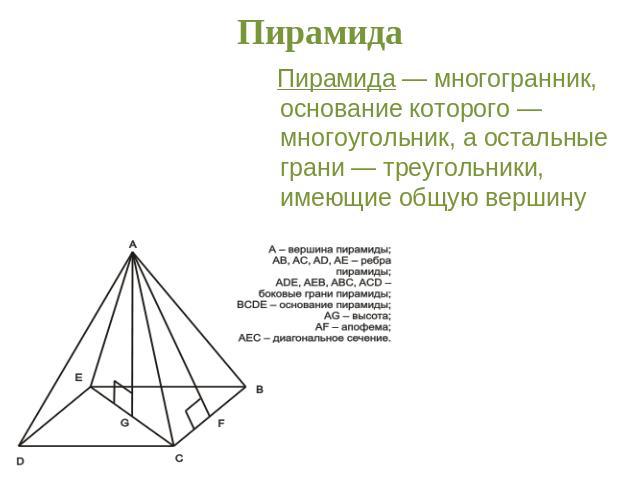
Пирамида Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину

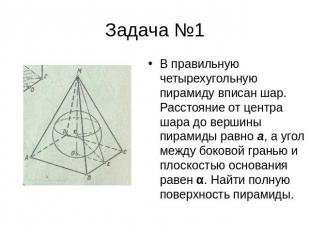
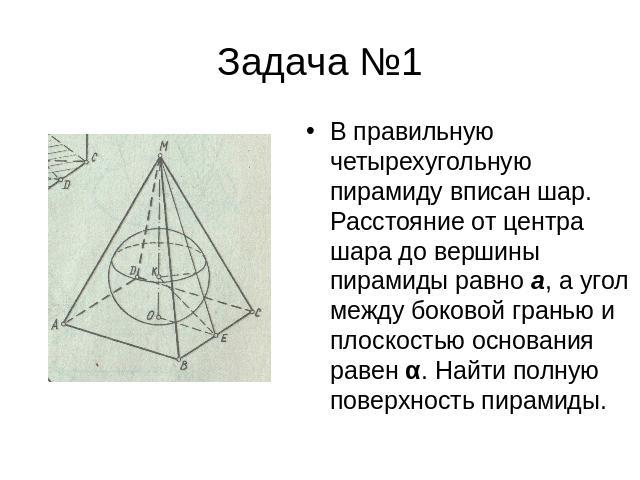
Задача №1 В правильную четырехугольную пирамиду вписан шар. Расстояние от центра шара до вершины пирамиды равно a, а угол между боковой гранью и плоскостью основания равен α. Найти полную поверхность пирамиды.

Решение.

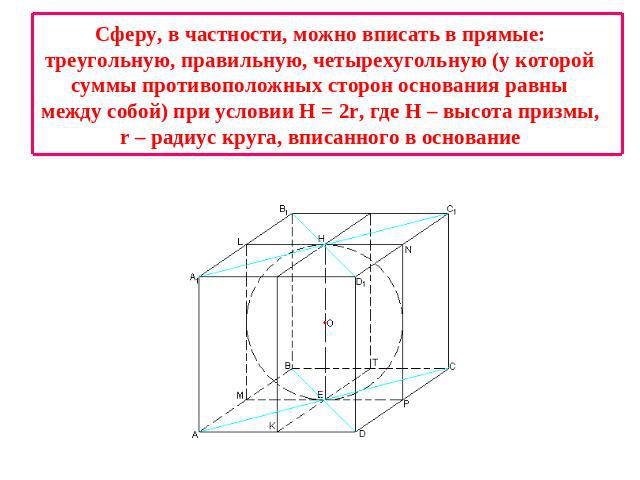
Сферу, в частности, можно вписать в прямые: треугольную, правильную, четырехугольную (у которой суммы противоположных сторон основания равны между собой) при условии Н = 2r, где Н – высота призмы, r – радиус круга, вписанного в основание

Конус Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.

В любой конус (прямой круговой) можно вписать шар При этом каждая образующая конуса является касательной к поверхности шара, и плоскость основания конуса касается поверхности шара.

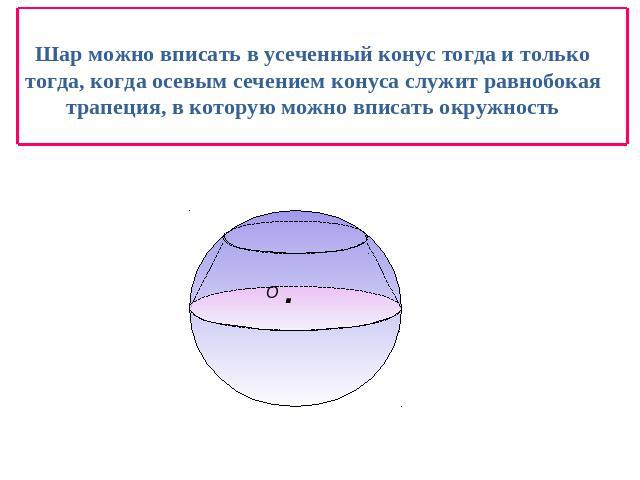
Шар можно вписать в усеченный конус тогда и только тогда, когда осевым сечением конуса служит равнобокая трапеция, в которую можно вписать окружность

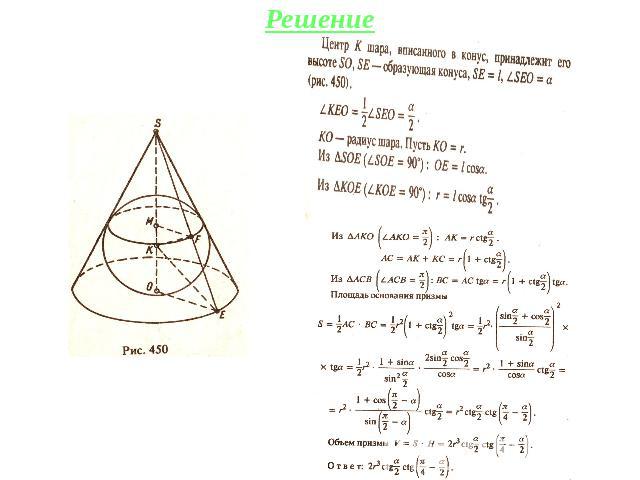
Задача №3 Образующая конуса равна l и составляет с плоскостью основания угол α. В этот конус вписан шар, а в шар вписана правильная треугольная призма, у которой все ребра равны между собой. Найти объем призмы.

Решение

В своей работе мы: Расширили и углубили свои знания по данной теме;Применили на практике теоретические основы;Надеемся, что навыки, полученные в процессе работы, помогут при сдаче экзаменов и при поступлении в ВУЗ

Анализ исследовательской деятельности учащихся на основе анкетирования Исследовательская работа является более результативной, чем традиционные уроки У учащихся формируются новые умения по самостоятельному добыванию и осмыслению знаний Метод исследовательской деятельности может использоваться в учебном процессе для решения различных проблемных задач, в т.ч. для работы над новыми темами Организация и проведение данного метода требует обоснованного и разумного подхода к познавательной деятельности. Такая деятельность не может проводиться, превращаясь в нечто повседневное; она должна являть собой праздник знаний, определенные вехи в изучении такой интересной и замечательной науки, какой является математика.

Итоги использования метода исследовательской деятельности учащихся по математике роль математики как учебного предмета чрезвычайно велика в плане формирования мировоззрения и творческого мышления учащихся;знания, твердые основы которых формируются при изучении математики в школе, должны быть максимально приближенны к реальной жизни и повседневной практике;изучение математики должно осуществляться так, чтобы учащиеся видели науку в постоянном развитии;обучение математики в школе должны осуществлять учителя, умеющие проводить педагогические исследования и способные организовать исследовательскую деятельность учащихся для реализации процесса углубленного познания математики.Т.о., исследовательская деятельность в осуществлении профильного обучения является инновационной технологией в работе с учащимися, которая позволяет объединить в единое целое учебный материал и методику преподавания математики. «Ученик – это не сосуд, который надо заполнить, а факел, который надо зажечь»