Презентация на тему: Симметрия

Симметрия.

Симметрия - (др.-греч. συμμετρία), в широком смысле — неизменность при каких-либо преобразованиях. Так, например, сферическая симметрия тела означает, что вид тела не изменится, если его вращать в пространстве на произвольные углы (сохраняя одну точку на месте). Двусторонняя симметрия означает, что правая и левая сторона относительно какой-либо плоскости выглядят одинаково.Отсутствие или нарушение симметрии называется асимметрией.Виды симметрий.Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′. Центральная симметрия с центром в точке A обычно обозначается через ZA, в то время как обозначение SA можно перепутать с осевой симметрией.Осевая симметрия — тип симметрии, имеющий два несколько отличающихся определения:Отражательная симметрия. В математике (точнее, евклидовой геометрии) осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две — в плоскости фигуры), если это не квадрат.Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но конус будет.Применительно к плоскости эти оба вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).Иногда вводят также (осевую) симметрию некоторого порядка:Осевая симметрия n-го порядка - симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Zn. Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка.

Общие свойства центральной симметрии. Центральная симметрия является движением (изометрией).В n-мерном пространстве центральную симметрию можно представить как композицию n последовательных отражений относительно n взаимно перпендикулярных гиперплоскостей, проходящих через центр симметрии. В частности В чётномерных пространствах центральная симметрия сохраняет ориентацию, а в нечётномерных — не сохраняет.Центральную симметрию можно представить также как гомотетию с центром A и коэффициентом −1 Композиция двух центральных симметрий — параллельный перенос на удвоенный вектор из первого центра во второй

Свойства центральной симметрии. Н а п р я м о йВ одномерном пространстве (на прямой) центральная симметрия является зеркальной симметрией. Н а п л о с к о с т иНа плоскости (в 2-мерном пространстве) симметрия с центром A представляет собой поворот на 180° с центром A. Центральная симметрия на плоскости, как и поворот, сохраняет ориентацию.В т р ё х м е р н о м п р о с т р а н с т в еЦентральную симметрию в трёхмерном пространстве называют также сферической симметрией.Её можно представить как композицию отражения относительно плоскости, проходящей через центр симметрии, с поворотом на 180° относительно прямой, проходящей через центр симметрии и перпендикулярной вышеупомянутой плоскости отражения.В ч е т ы р ё х м е р н о м п р ос т р а н с т в еВ 4-мерном пространстве центральную симметрию можно представить как композицию двух поворотов на 180° вокруг двух взаимно перпендикулярных плоскостей (перпендикулярных в 4-мерном смысле, проходящих через центр симметрии.

Примеры симметрии в архитектуре.

Симметрия в природе.

Симметрия в искусстве.

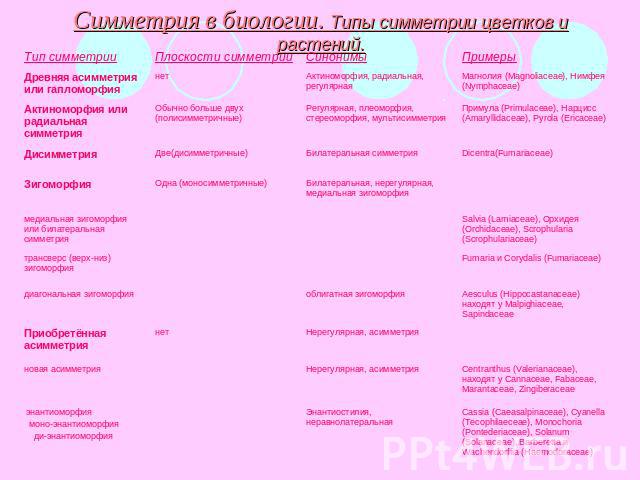
Симметрия в биологии. Типы симметрии цветков и растений.

Симметрия в физике. Симметрия (симметрии) - одно из фундаментальных понятий в современной физике, играющее важнейшую роль в формулировке современных физических теорий. Симметрии, учитываемые в физике, довольно разнообразны, начиная с симметрий обычного трехмерного "физического пространства" (такими, например, как зеркальная симметрия), кончая более абстрактными и менее наглядными.Некоторые симметрии в современной физике считаются точными, другие - лишь приближенными. Также важную роль играет концепция спонтанного нарушения симметрии.Исторически использование симметрии в физике прослеживается с древности, но наиболее революционным для физики в целом, по-видимому, стало применение такого принципа симметрии, как принцип относительности (как у Галилея, так и у Пуанкаре-Лоренца-Эйнштейна), ставшего затем как бы образцом для введения и использования в теорфизике других принципов симметрии (первым из которых стал, по-видимому, принцип общековариантности, являющимся достаточно прямым расширением принципа относительности и приведшего к общей теории относительности Эйнштейна).В теоретической физике, поведение физической системы описывается обычно некоторыми уравнениями. Если эти уравнения обладают какими-либо симметриями, то часто удаётся упростить их решение путём нахождения сохраняющихся величин (интегралов движения). Так, уже в классической механике формулируется теорема Нётер, которая каждому типу непрерывной симметрии сопоставляет сохраняющуюся величину. Из неё, например, следует, что инвариантность уравнений движения тела с течением времени приводит к закону сохранения энергии; инвариантность относительно сдвигов в пространстве — к закону сохранения импульса; инвариантность относительно вращений — к закону сохранения момента импульса.

© Екатерина Сёмина 2009, апрель.