Презентация на тему: Симметрия

Симметрия Работа ученика 9-а класса МОУ СОШ №1 г ТындыФомина Александра ПетровичаРуководитель Собко Людмила Александровна

Математика владеет не только истиной, но и красотой … Б. Рассел

Основные вопросыСимметрия- это гармония и красота? Равновесие? Устойчивость?Зачем человеку нужно знать о симметрии?

Цель работыИзучить тему «Симметрия на плоскости и в пространстве»Исследовать вопрос «Симметрия в окружающем нас мире»

Основные понятияСимметрия относительно точкиСимметрия относительно прямойСимметрия относительно плоскостиСимметрия в пространствеГеометрический подход к симметрииСимметрия в окружающем нас мире

Основные понятия. Симметрия— это гармония формы и определенный порядок. Но это слишком общее разъяснение. Каким образом можно конкретизировать понятие симметрии? Нужно привлечь математику, точнее, геометрию, и попытаться классифицировать различные виды симметрии. Прежде чем перейти к общепринятой терминологии, обратимся к рисункам, которые помогут уяснить задачу классификации симметрии.

СИММЕТРИЯ (от греч. symmetria — соразмерность), в широком смысле — инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований (т. е. изменений ряда физических условий). Симметрия лежит в основе законов сохранения.

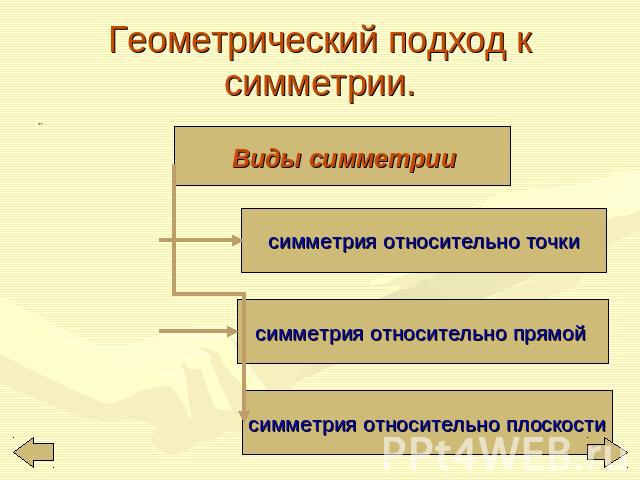
Геометрический подход к симметрии.,. Виды симметрии симметрия относительно точки симметрия относительно прямой симметрия относительно плоскости

Симметрия относительно точки. ЦЕНТРАЛЬНАЯ СИММЕТРИЯ — симметрия относительно точки, которая задается следующим образом: :1. Зададим фиксированную точку О, которая называется центром симметрии;2. Произвольной точке А поставим в соответствие точку А1, принадлежащую прямой АО, так что ОА = ОА1. Точка А симметрична точке А1 относительно точки О. Точки В и B1 симметричны, относительно точки 0.3. Пусть F — данная фигура и О — центр симметрии. Преобразование фигуры F в фигуру F1 при котором каждая ее точка А переходит в точку А1 фигуры F1 симметричную относительно точки О, называется преобразованием симметрии относительно точки О.

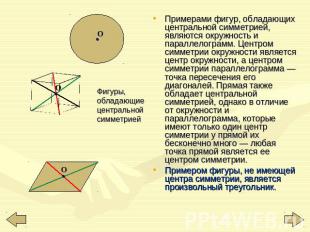
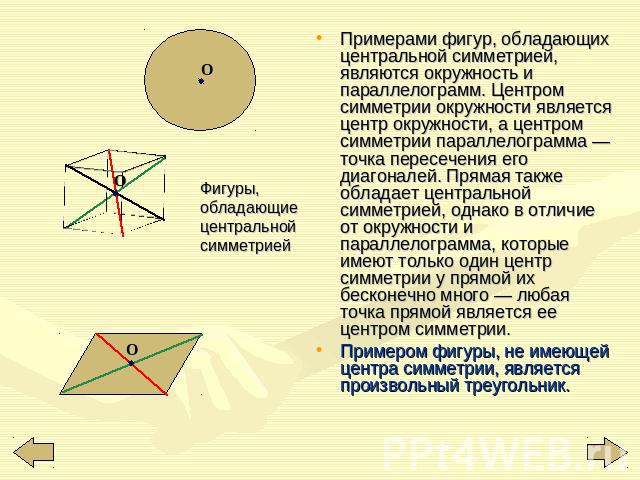
Фигуры, обладающие центральной симметрией Примерами фигур, обладающих центральной симметрией, являются окружность и параллелограмм. Центром симметрии окружности является центр окружности, а центром симметрии параллелограмма — точка пересечения его диагоналей. Прямая также обладает центральной симметрией, однако в отличие от окружности и параллелограмма, которые имеют только один центр симметрии у прямой их бесконечно много — любая точка прямой является ее центром симметрии. Примером фигуры, не имеющей центра симметрии, является произвольный треугольник.

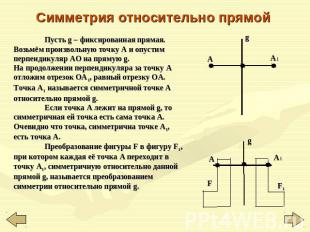
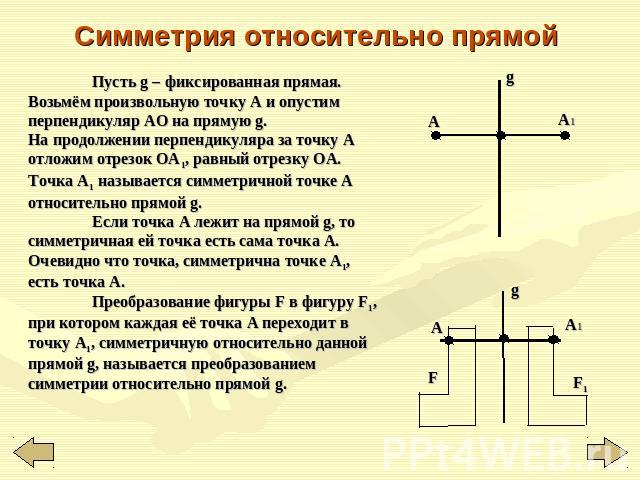
Симметрия относительно прямой Пусть g – фиксированная прямая. Возьмём произвольную точку A и опустим перпендикуляр AO на прямую g. На продолжении перпендикуляра за точку A отложим отрезок OA1, равный отрезку ОA. Точка A1 называется симметричной точке A относительно прямой g. Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A. Очевидно что точка, симметрична точке A1, есть точка A. Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.

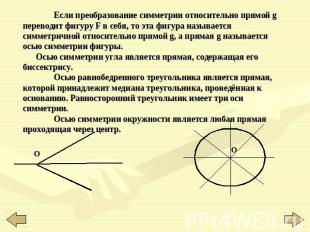
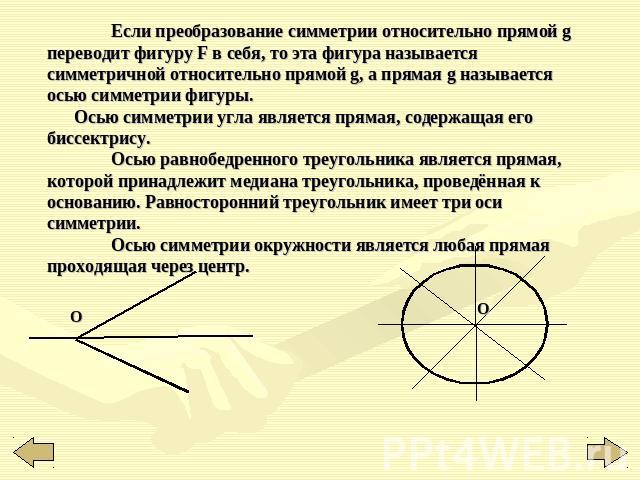
Если преобразование симметрии относительно прямой g переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой g, а прямая g называется осью симметрии фигуры. Осью симметрии угла является прямая, содержащая его биссектрису. Осью равнобедренного треугольника является прямая, которой принадлежит медиана треугольника, проведённая к основанию. Равносторонний треугольник имеет три оси симметрии. Осью симметрии окружности является любая прямая проходящая через центр.

ЭллипсИмеет центр симметрии и две оси симметрии

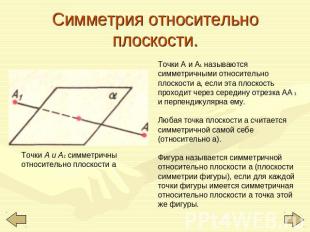
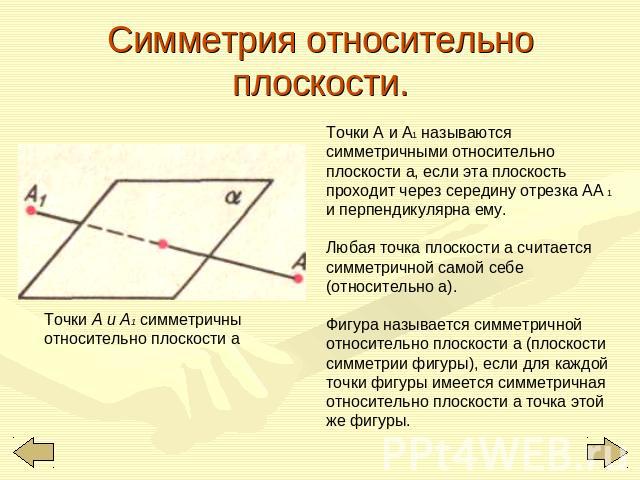
Симметрия относительно плоскости. Точки А и A1 симметричны относительно плоскости а Точки А и А1 называются симметричными относительно плоскости а, если эта плоскость проходит через середину отрезка АА 1 и перпендикулярна ему. Любая точка плоскости а считается симметричной самой себе (относительно а).Фигура называется симметричной относительно плоскости а (плоскости симметрии фигуры), если для каждой точки фигуры имеется симметричная относительно плоскости а точка этой же фигуры.

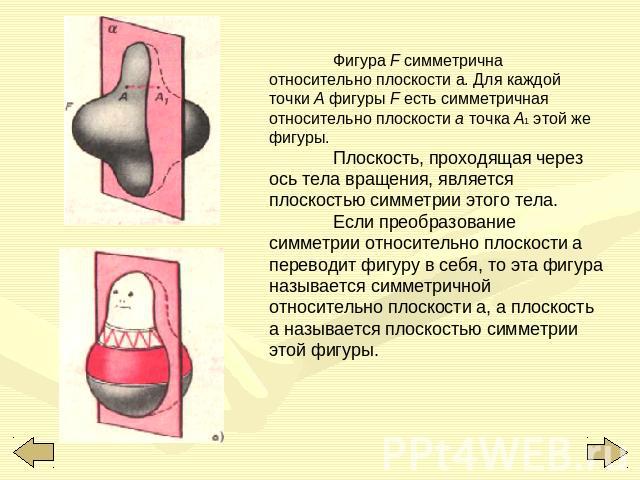
Фигура F симметрична относительно плоскости а. Для каждой точки А фигуры F есть симметричная относительно плоскости а точка А1 этой же фигуры. Плоскость, проходящая через ось тела вращения, является плоскостью симметрии этого тела. Если преобразование симметрии относительно плоскости а переводит фигуру в себя, то эта фигура называется симметричной относительно плоскости а, а плоскость а называется плоскостью симметрии этой фигуры.

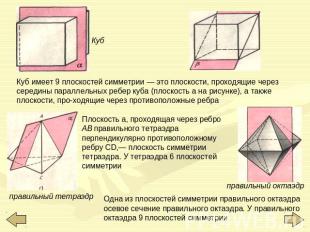
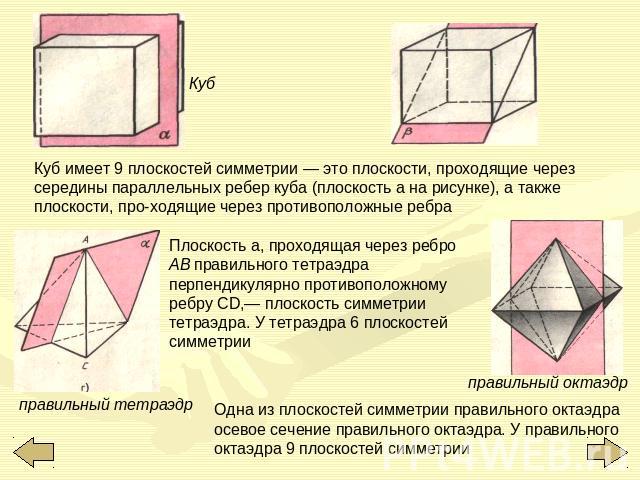
Куб имеет 9 плоскостей симметрии — это плоскости, проходящие через середины параллельных ребер куба (плоскость а на рисунке), а также плоскости, проходящие через противоположные ребра Плоскость а, проходящая через ребро АВ правильного тетраэдра перпендикулярно противоположному ребру CD,— плоскость симметрии тетраэдра. У тетраэдра 6 плоскостей симметрии Одна из плоскостей симметрии правильного октаэдра осевое сечение правильного октаэдра. У правильного октаэдра 9 плоскостей симметрии

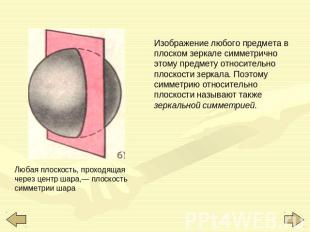
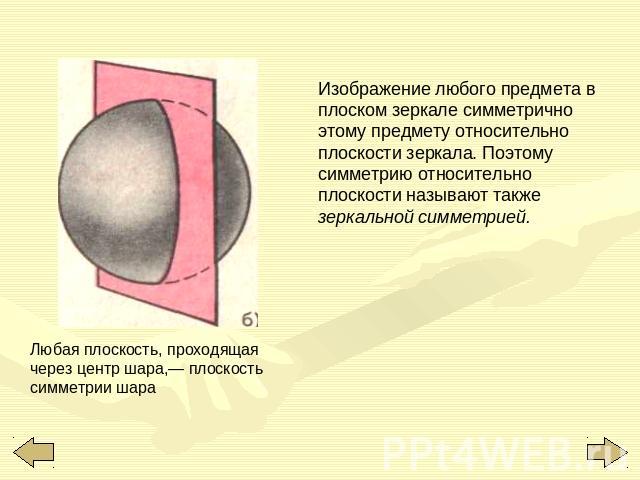
Изображение любого предмета в плоском зеркале симметрично этому предмету относительно плоскости зеркала. Поэтому симметрию относительно плоскости называют также зеркальной симметрией. Любая плоскость, проходящая через центр шара,— плоскость симметрии шара

Симметрия в пространстве а) Центральная симметрия Как и в случае плоскости, точки А и А1 в пространстве называются симметричными относительно точки О, если О — середина отрезка АА1. Фигура называется симметричной относительно точки О (центра симметрии фигуры), если для каждой ее точки имеется симметричная относительно центра О точка этой же фигуры

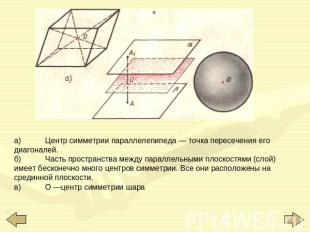
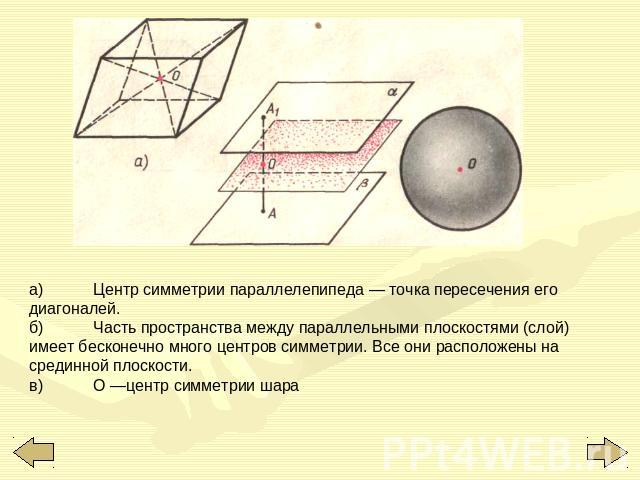
а)Центр симметрии параллелепипеда — точка пересечения его диагоналей.б)Часть пространства между параллельными плоскостями (слой) имеет бесконечно много центров симметрии. Все они расположены на срединной плоскости.в)О —центр симметрии шара

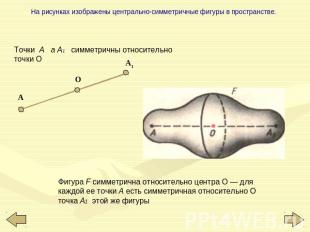
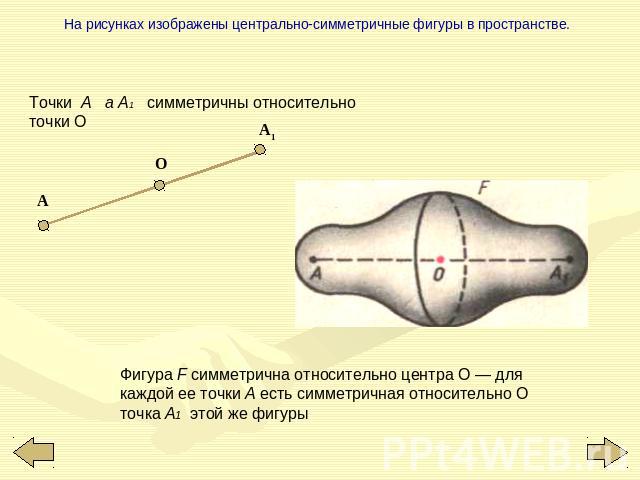
На рисунках изображены центрально-симметричные фигуры в пространстве. Точки А а А1 симметричны относительно точки О Фигура F симметрична относительно центра О — для каждой ее точки А есть симметричная относительно О точка А1 этой же фигуры

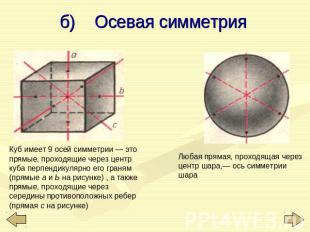
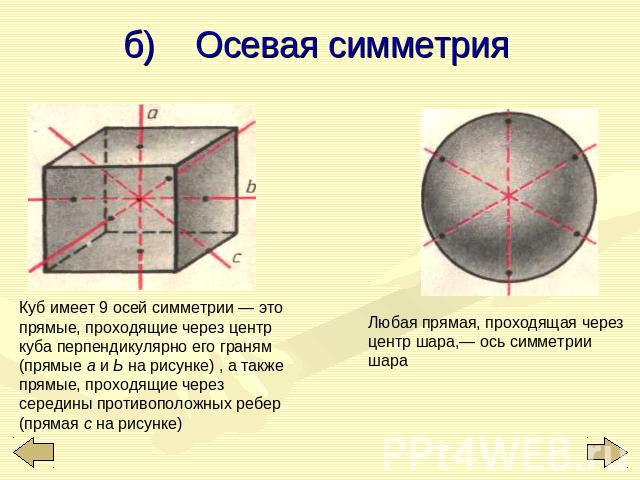
б) Осевая симметрия Куб имеет 9 осей симметрии — это прямые, проходящие через центр куба перпендикулярно его граням (прямые а и Ь на рисунке) , а также прямые, проходящие через середины противоположных ребер (прямая с на рисунке) Любая прямая, проходящая через центр шара,— ось симметрии шара

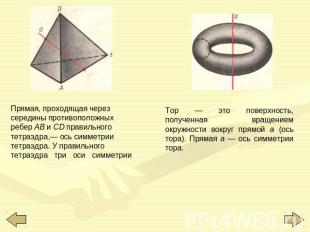
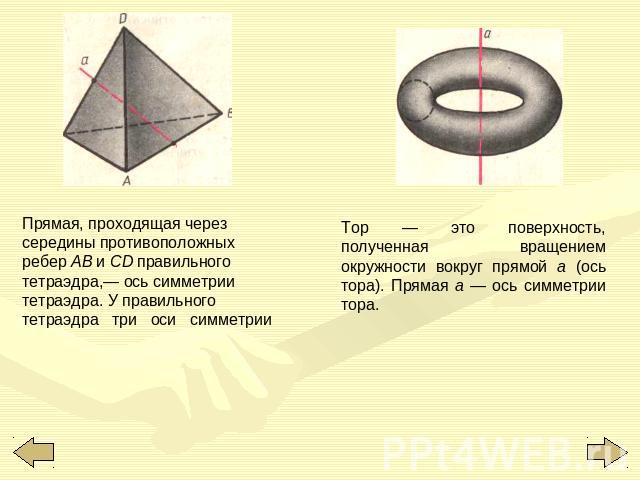
Прямая, проходящая через середины противоположных ребер АВ и CD правильного тетраэдра,— ось симметрии тетраэдра. У правильного тетраэдра три оси симметрии Тор — это поверхность, полученная вращением окружности вокруг прямой а (ось тора). Прямая а — ось симметрии тора.

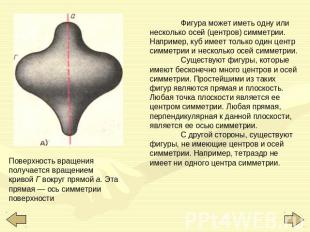
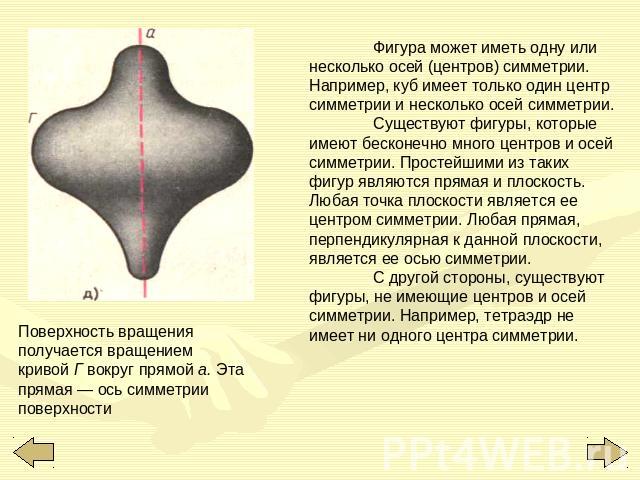
Поверхность вращения получается вращением кривой Г вокруг прямой а. Эта прямая — ось симметрии поверхности Фигура может иметь одну или несколько осей (центров) симметрии. Например, куб имеет только один центр симметрии и несколько осей симметрии. Существуют фигуры, которые имеют бесконечно много центров и осей симметрии. Простейшими из таких фигур являются прямая и плоскость. Любая точка плоскости является ее центром симметрии. Любая прямая, перпендикулярная к данной плоскости, является ее осью симметрии. С другой стороны, существуют фигуры, не имеющие центров и осей симметрии. Например, тетраэдр не имеет ни одного центра симметрии.

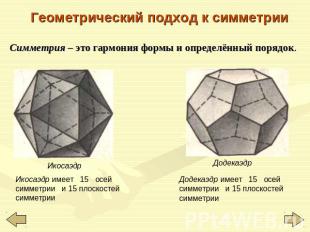
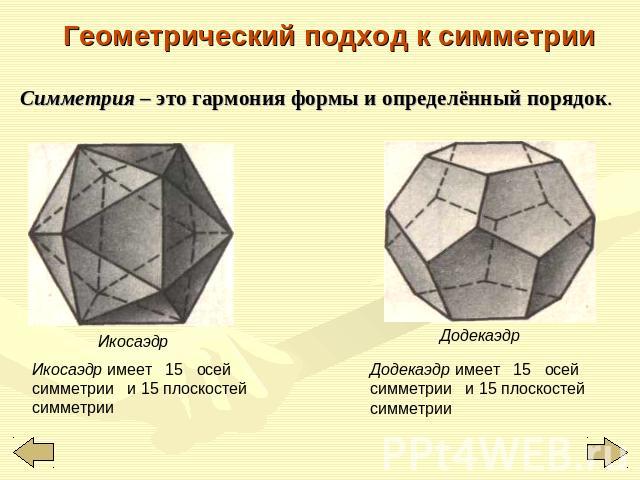
Геометрический подход к симметрии Симметрия – это гармония формы и определённый порядок. Икосаэдр имеет 15 осей симметрии и 15 плоскостей симметрии Додекаэдр имеет 15 осей симметрии и 15 плоскостей симметрии

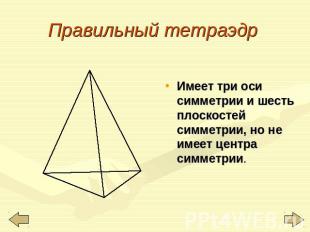
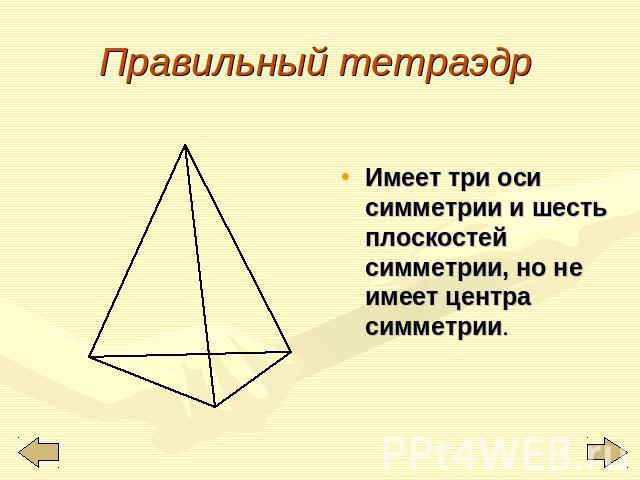
Правильный тетраэдр Имеет три оси симметрии и шесть плоскостей симметрии, но не имеет центра симметрии.

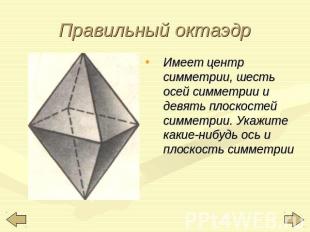
Правильный октаэдр Имеет центр симметрии, шесть осей симметрии и девять плоскостей симметрии. Укажите какие-нибудь ось и плоскость симметрии

Звездчатый октаэдр Кеплера Можно рассматривать как объединение двух правильных тетраэдров. Имеет центр симметрии и несколько осей и плоскостей симметрии

Рисунок имеет три оси симметрии. Треугольник Рело, как и окружность,— кривая постоянной ширины, равной а. Это означает, что его можно вращать между двумя параллельными прямыми, расстояние между которыми равно а. Периметр треугольника Рело, т. е. сумма длин дуг АВ, ВС и CD, равен паЕще одна кривая постоянной ширины, равной а = НЕ. Строится она так. Берется равносторонний треугольник ABC и с центрами в точках А, В и С проводятся дуги НК, DE и FQ окружностей произвольного радиуса АН. Затем с центрами в этих же точках проводятся дуги EF, GH и KD окружностей радиуса АЕ. Эта кривая имеет три оси симметрии. Длина кривой равна па

Кривая Вавиани Кривая Вавиани — линия пересечения сферы радиуса а и цилиндра диаметра а. Имеет две плоскости симметрии. Предложена итальянским архитектором Вавиани (1622—1703) для окна в сферическом куполе здания. Попытайтесь найти расположение плоскостей симметрии кривой Вавиани

Симметрия в окружающем нас мире. Всё красивое радует нас. Мы невольно отмечаем для себя красивый закат, удивительные листья растений, строгие формы кристаллов. Когда мы рассказываем об увиденном, то мысленно всё ещё созерцаем. Постепенно у нас формируется картина окружающего мира, мы находим общее в различных предметах. Например, лист клевера и лист клена различны по форме, но их объединяет что-то общее. Наверное каждый скажет: эти листья имеют симметрию - у них есть ось симметрии. Симметрия наблюдается не только у листьев. Любуясь закатом солнца на море, мы также видим симметрию- направо и налево от солнца всё одинаково. Симметрия есть на дошедших до нас картинах древних художников. Очень часто симметрия используется в архитектуре.

Симметрия широко распространена в природе. Ее можно наблюдать в форме листьев и цветов растений, в расположении различных органов животных, в форме кристаллических тел.Симметрия широко используется на практике, в строительстве и технике

На рисунках вы можете обнаружить соразмерность форм, правильное расположение частей предметов, что можно рассматривать как определённую форму симметрии.

Ведь и назначение и цель гармонии - упорядочить части, вообще говоря, различные по природе, неким совершенным соотношением так, чтобы они одна другой соответствовали, создавая красоту. Л.Б. Альберти 

Я в листочке, я в кристалле,Я в живописи, архитектуре,Я в геометрии, я в человеке.Одним я нравлюсь, другиеНаходят меня скучной.Но все признают, чтоЯ – элемент красоты.

Математики шутят… Шутка об осевой симметрииОднажды чужеземец, восхищённый красотой знаменитого бухарского минарета Калян, воскликнул:Как вы строите такие высокие минареты?Очень просто, - ответил ходжа Насреддин и, не преминув блеснуть своим обычным остроумием, пояснил: «Сначала выкапываем глубокий колодец, а потом выворачиваем его наизнанку».

Информационные ресурсы Погорелов А.В. Геометрия 7-11, Геометрия 10-11Руденко В.Н. Бахулин Г.А. Геометрия 7-9Атанасян Л.С. Геометрия 7-9, Геометрия 10-11Большая энциклопедия Кирилла и Мефодия 2006Зенкевич И.Г. Эстетика урока математикиЯшекова Г. Математика справочник школьникаБутузов В.Ф. Математика 11