Презентация на тему: Треугольники

Учебный план профильного обучения Итоговое повторение планиметрии к ГИАВыполнила Червина Н.П., учитель математики моу сош №5 г. Михайловки Волгоградской области

Итоговое повторение курса геометрии мы начнём с повторения планиметрии. Основные факты планиметрии и применяемые в ней методы можно сгруппировать по следующим темам: «Треугольники», «Четырёхугольники, многоугольники», «Окружность». Цель итогового повторения: - восстановление в памяти учащихся основного материала;- обобщение, уточнение и систематизация знаний по планиметрии.Тема урока: «Треугольники»Цель урока: - повторение теоретического материала;-обобщение навыка решения задач;

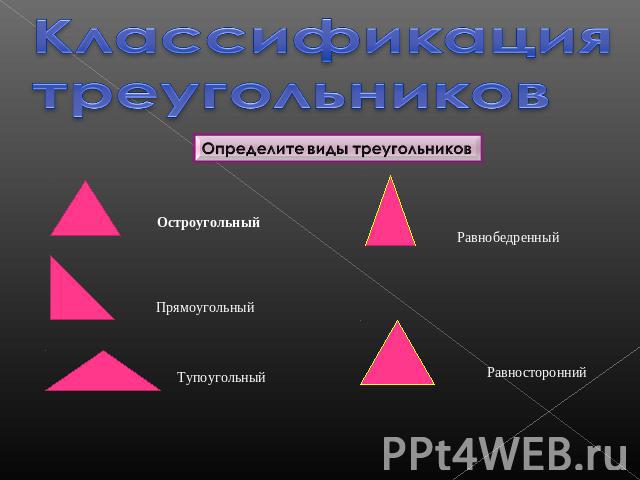
Классификация треугольников Определите виды треугольниковОстроугольныйПрямоугольныйТупоугольныйРавнобедренныйРавносторонний

Прямоугольный Треугольник

Площадь треугольника

Решение косоугольных треугольников

Подобие треугольников

Свойства медиан и биссектрис

Задача. Найдите высоту прямоугольного треугольника, проведенную к гипотенузе, если биссектриса острого угла делит катет на отрезки, равные 2 и 4. Решение. 1) По свойству биссектрисыИмеем АВ:ВС=2:1, тогда, если ВС=х,То АВ=2х, АС= , АС=6,Тогда =6,откуда , то есть ВС= , АВ= .2) Найдём высоту СН:S =0,5·АС·ВС=0,5АВ·СН, откуда СН= Ответ: 3

Задача. Из вершины В параллелограмма АВСD проведён луч, который пересекает СD в (·)N и диагональ АС в (·)Т.Площадь треугольника ВСТ равна 12,а СТN-8.Найти площадь параллелограмма АВСD. Решение: 12=1∕2∙ВТ·h, ВТ=24∕ h и 8=1∕ 2·ТN∙h, ТN=16∕ h,ВТ:ТN=24:16=3:2.ТреугольникиАВТ и СТN подобны(по двум углам), значит отношение их площадей равно kⁿ, где k=2, т.е.9∕4. SАВТ:SСТN=9:4, SАВТ=8∙9:4=18,SАВС=18+12=30,SАВСD=30·2=60Ответ: 60

Задача. Дан равнобедренный треугольник АВС, АС=АВ=20,высоты ВК и АН пересекаются в (∙)О, Площадь АВС равна160. Найдите площадь треугольника АВО. Решение: SАВС=1/2·АС∙ВК160=1/2·20∙ВК, ВК=160/10=16.Из АВК: АК=12( по Т. Пиф.)АН-высота-биссектрисса,АО-бис., ОК:ОВ=АК:АВ, еслиОК=х, то ОВ=16-х, подставляемОК=6, ОВ=10.SАОК=1/2·ОК∙ АК=1/2∙6·12=36SАОВ=SАВК-SАОК=1/2∙16·12-36=60Ответ: 60