Презентация на тему: Декартовы координаты в пространстве

Работа Учителя математики « МОУ СОШ №9 с. Нины Советского районаДиденко Н.Н.

Задачи урока 1.Показать, максимально используя наглядность, что координаты в пространстве вводятся столь же просто и естественно, как и координаты на плоскости.2.Применение формул к решению задач.

Урок по теме Декартовы координаты в пространстве Р. Декарт — французский ученый (1596— 1650)Декарт был крупнейшим философом и математиком своего времени. В основе его философии лежал материализм. Самым известным трудом Декарта является его “Геометрия”. Декарт ввел систему координат, которой пользуются все и в настоящее время. Он установил соответствие между числами и отрезками прямой и таким образом ввел алгебраический метод в геометрию. Эти открытия Декарта дали огромный толчок развитию как геометрии, так и другим разделам математики .

МотивацияВ своё время Рене Декарт сказал:“… потомки будут благодарны мне не только за то, что я сказал, но и за то, что я не сказал и тем самым дал им возможность и удовольствие додуматься до этого самостоятельно”.

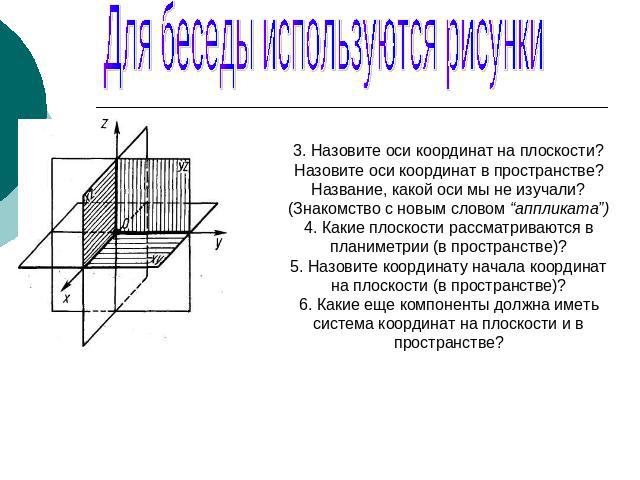
Для беседы используются рисунки3. Назовите оси координат на плоскости? Назовите оси координат в пространстве? Название, какой оси мы не изучали? (Знакомство с новым словом “аппликата”)4. Какие плоскости рассматриваются в планиметрии (в пространстве)?5. Назовите координату начала координат на плоскости (в пространстве)?6. Какие еще компоненты должна иметь система координат на плоскости и в пространстве?

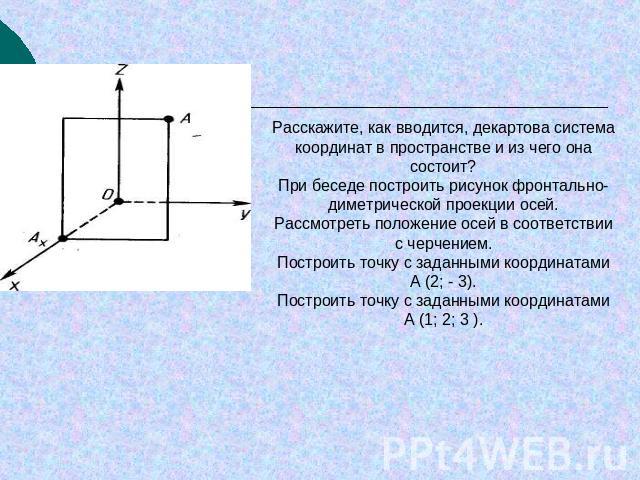
Расскажите, как вводится, декартова система координат в пространстве и из чего она состоит?При беседе построить рисунок фронтально-диметрической проекции осей.Рассмотреть положение осей в соответствии с черчением.Построить точку с заданными координатами А (2; - 3).Построить точку с заданными координатами А (1; 2; 3 ).

Основные понятия декартовых координат.

формула расстояния между точками

Координаты середины отрезка.

Вопросы: 1) Чему будут равны линейные размеры( или измерения) этого параллелепипеда? 2) Каковы координаты всех восьми его вершин?3)Для любой ли ( упорядоченной ) тройки чисел (х; у;z) в пространстве найдется точка с такими координатами?

Условие задачиНайдите расстояние от точки А( 1; 2; -3) до:1) координатных плоскостей;2) осей координат;3) начала координат.

Решение задачи Указание: строим координатный параллелепипед и находим нужные расстояния:1)ААху =IzI =3 ; ААхz= I yI=2 ; AAyz = I X I = 1. 2) по теореме Пифагора аналогично