Презентация на тему: Числовые характеристики (параметры) распределений случайных величин

Числовые характеристики (параметры) распределений случайных величин

литература

Математическое ожидание: центр <<тяжести >> распределения Дискретные распределения Непрерывные распределения

Виды параметров МоментыначальныецентральныеПараметры сдвига математическое ожиданиемедианамодаПараметры формы дисперсияасимметрия эксцесс

Моменты

Связь между центральными и начальными моментами Применим формулу бинома Ньютона

Возьмем мат. ожидание от левой и правой частей этого выражения и получим выражение, связывающее центральные и начальные моменты

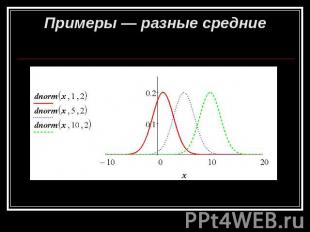
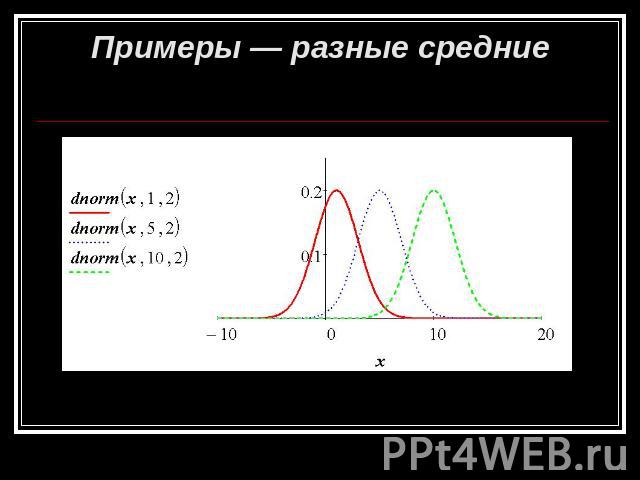
Примеры — разные средние

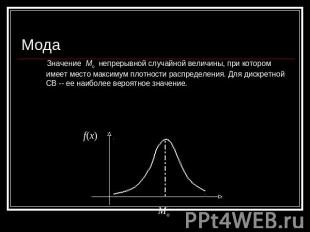
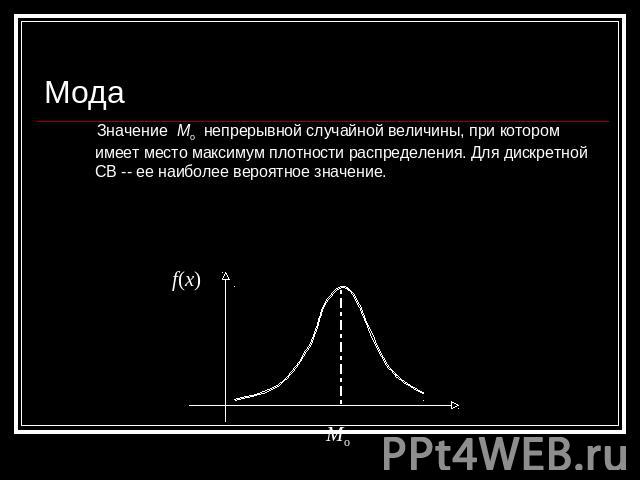
Мода Значение Mo непрерывной случайной величины, при котором имеет место максимум плотности распределения. Для дискретной СВ -- ее наиболее вероятное значение. f(x)

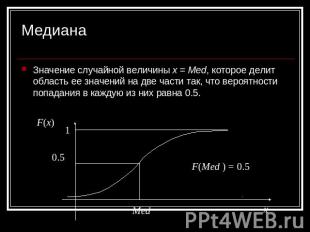
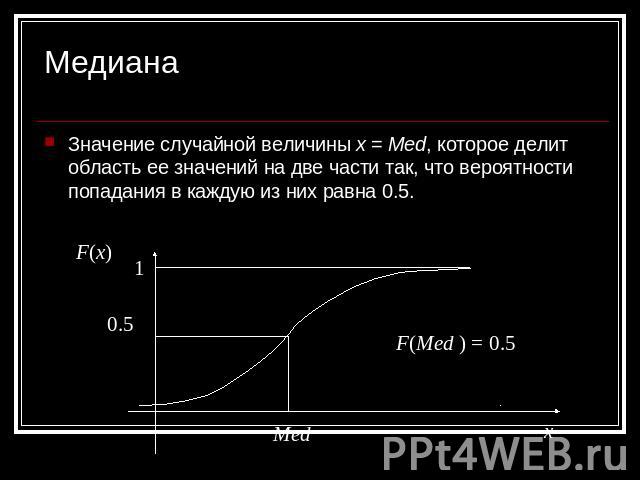
Медиана Значение случайной величины x = Med, которое делит область ее значений на две части так, что вероятности попадания в каждую из них равна 0.5. F(Med ) = 0.5 Med F(x)

Параметры формы (масштаба) Дисперсия Dx и среднеквадратичное отклонение 2 Дискретные СВ Непрерывные СВ

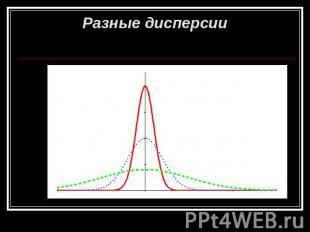
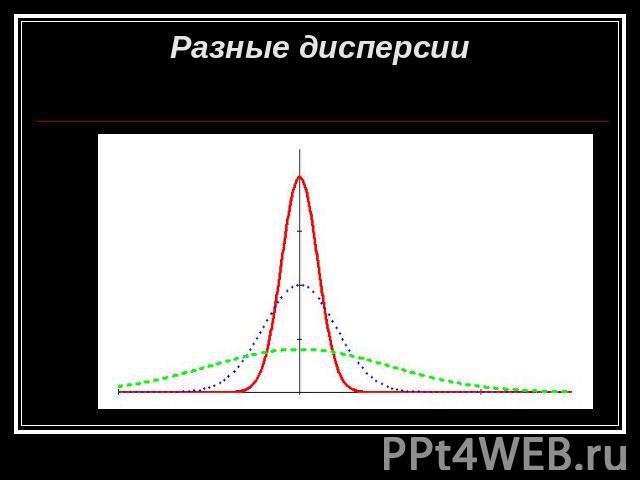
Разные дисперсии

Свойства дисперсии

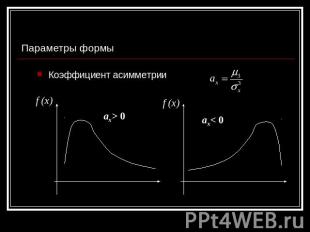
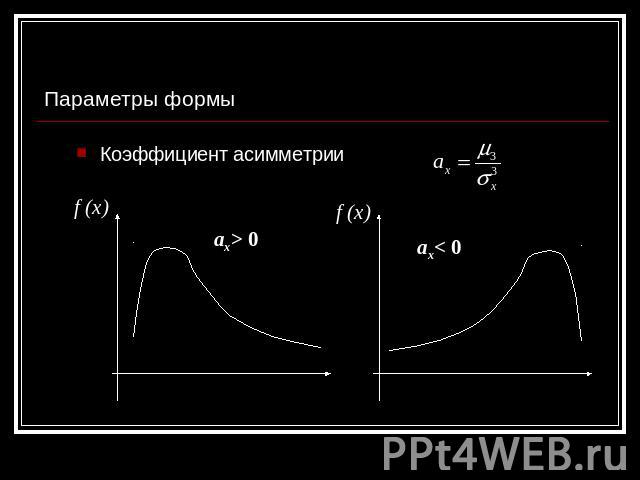
Параметры формы Коэффициент асимметрии f (x) ax> 0 f (x) ax< 0

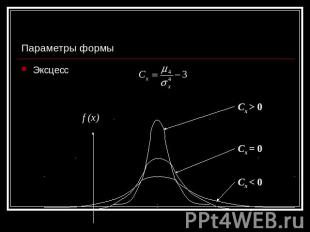
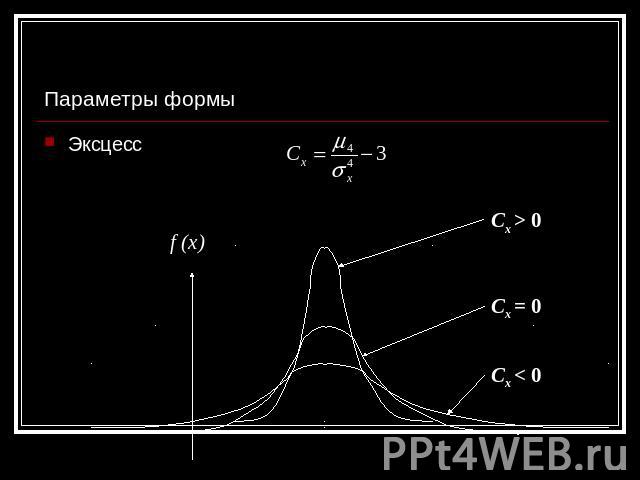
Параметры формы Эксцесс f (x) Cx > 0 Cx = 0 Cx < 0

Основные распределения и их свойства

Вырожденное распределение(Распределение константы) Распределение Бернулли (Распределение индикатора события)

Равномерное распределение