Презентация на тему: Случайные величины и их законы распределения

литература

Случайные величины и их законы распределения

Определение случайной величины это числовая функция, заданная на множестве элементарных событий с областью значений вИли в

СЛУЧАЙНОЕ СОБЫТИЕ теперь под случайным событием понимается попадание случайной величины в некоторое конечное или бесконечное числовое множество

Обычно рассматривают два вида случайных величин: дискретные и непрерывные.

Дискретная случайная величина принимает конечное или счетное множество значенийона используется при описании измерений, принимающих целочисленные значения:Число дефектных изделий в партии, число телефонных вызовов за смену,число неисправностей в приборе и т.д. и может быть записана в виде последовательности

Непрерывные случайные величины принимают любое значение в некотором интервале:продолжительность работы электрической лампы;дальность полета снаряда, уровень воды в половодье и т.д.

Закон распределения дискретной случайной величины Для полного описания дискретной случайной величины необходимо:Указать все её возможные значения.Задать вероятности, с которыми принимаются эти значения.

Ряд распределения

Функция распределения случайной величины

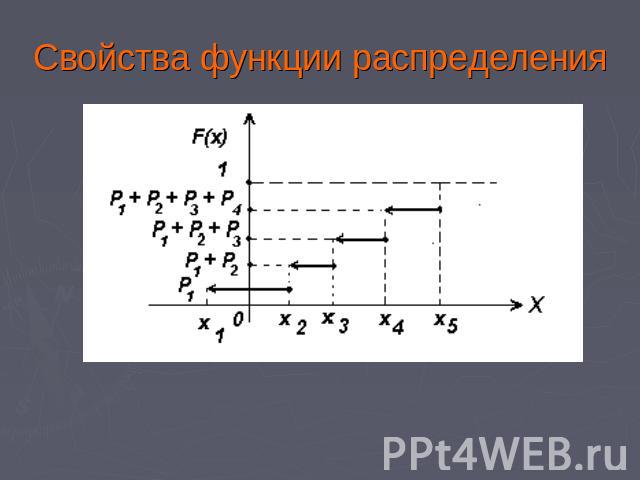
Свойства функции распределения

Свойства функции распределения

Свойства функции распределения Для дискретной СВ

Свойства функции распределения

Непрерывная случайная величина Случайная величина X называется непрерывной, если ее функцияраспределения непрерывна

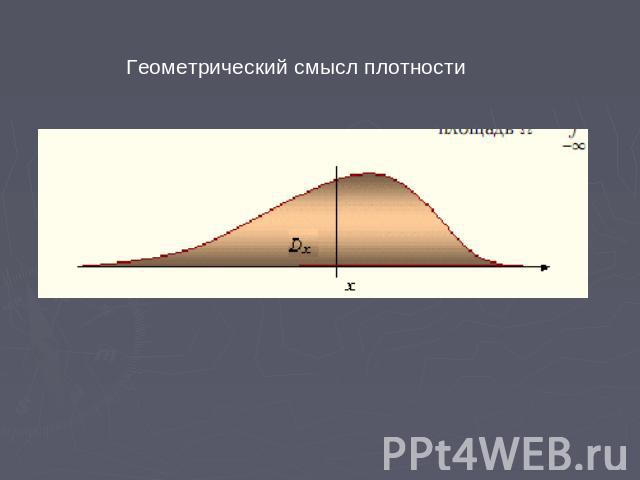
Геометрический смысл плотности

Примеры Вырожденное распределение(Распределение константы) Распределение Бернулли (Распределение индикатора события)

Равномерное распределение