Презентация на тему: Случайные величины: законы распределения

Случайные величины: законы распределения

Что было: понятие о случайной величине СЛУЧАЙНОЙ ВЕЛИЧИНОЙ называется величина, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которыезаранее не могут быть учтены.Функцией распределения случайной величины X называется функция F (x), выражающая для каждого x вероятность того, что случайная величина X примет значение, меньшее x F (x) = P (X < x).

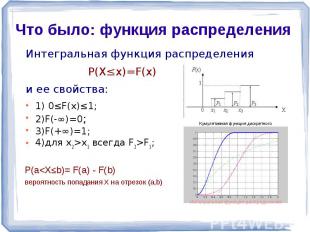
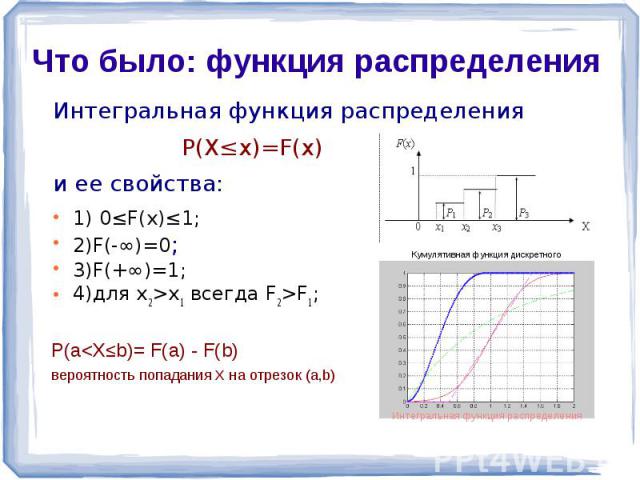
Интегральная функция распределения P(X≤x)=F(x) и ее свойства: 1) 0≤F(x)≤1; 2)F(-∞)=0; 3)F(+∞)=1; 4)для x2>x1 всегда F2>F1;

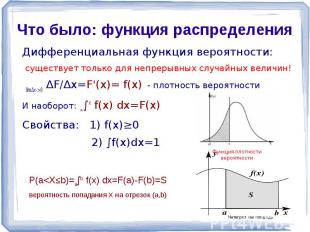
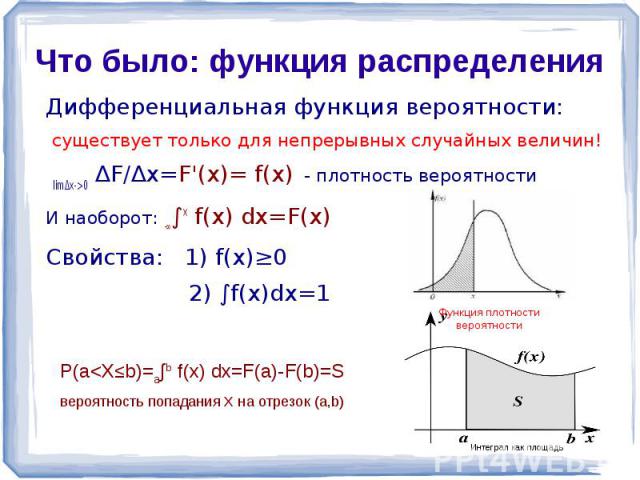
Что было: функция распределения Дифференциальная функция вероятности: существует только для непрерывных случайных величин! lim∆x->0 ∆F/∆x=F'(x)= f(x) - плотность вероятностиИ наоборот: -∞∫х f(x) dx=F(x)Свойства: 1) f(x)≥0 2) ∫f(x)dx=1

Характеристики функции распределения Дискретная случайная величинаМатематическое ожидание: М[x]=Дисперсия D[x]=Мода (значение с наибольшей вероятностью) Мо=Xi | p(xi)=pmaxМедиана Непрерывная случайная величинаМатематическое ожидание: M[X]= ДисперсияD[X]= Мода (значение с наибольшей плотностью вероятности)Мо=xi | f(xi)=maxМедиана

Знаем: какие бывают случайные величины; что такое интегральная (кумулятивная) функция распределения и распределение плотности вероятности; вероятность попадания Х на отрезок (а,b); как описать распределение F(x).Не знаем, какие бывают F(x)

Законы распределения случайных величин

Непрерывная случайная величина имеет равномерный закон распределения на (а,b), если ее плотность вероятности постоянна на этом отрезке и равна 0 вне его.Функция P(X<x)=F(X) имеет видF(x)=0 при x≤aF(x)=(x-a)/(b-a) при a<x≤bF(x)=1 при x>bМатематическое ожидание: M[x]=(a+b)/2Дисперсия: D[x]=(b-a)2/12

Равномерное распределение №2 Дискретная случайная величина имеет равномерное распределение, если ее функция вероятности на всей области определения (a,b) имеет видP(x)=1/n, где n — число исходовM[x]=(a+b)/2 - мат.ожиданиеD[x]=(n2-1)/12 - дисперсия

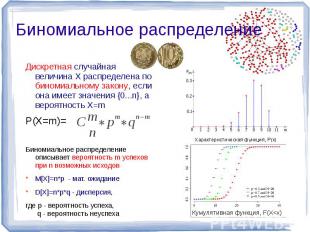
Биномиальное распределение Дискретная случайная величина X распределена по биномиальному закону, если она имеет значения {0...n}, а вероятность Х=m P(X=m)=Биномиальное распределение описывает вероятность m успехов при n возможных исходовM[X]=n*p - мат. ожиданиеD[X]=n*p*q - дисперсия,где p - вероятность успеха, q - вероятность неуспеха

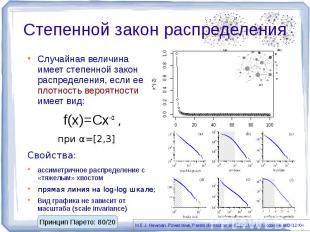
Степенной закон распределения Случайная величина имеет степенной закон распределения, если ее плотность вероятности имеет вид:f(x)=Cx-α , при α=[2,3]Свойства: ассиметричное распределение с «тяжелым» хвостомпрямая линия на log-log шкале;Вид графика не зависит от масштаба (scale invariance)

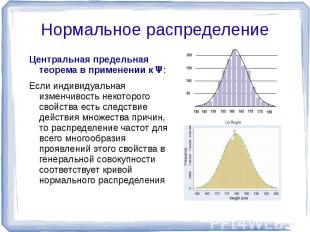
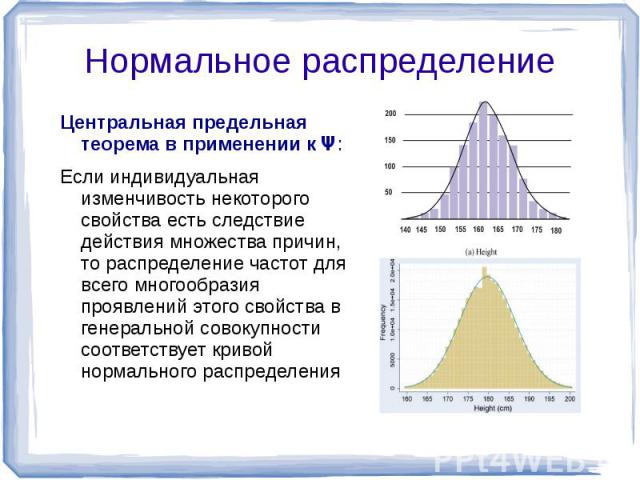
Центральная предельная теорема в применении к Ψ: Если индивидуальная изменчивость некоторого свойства есть следствие действия множества причин, то распределение частот для всего многообразия проявлений этого свойства в генеральной совокупности соответствует кривой нормального распределения

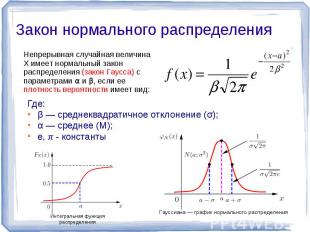
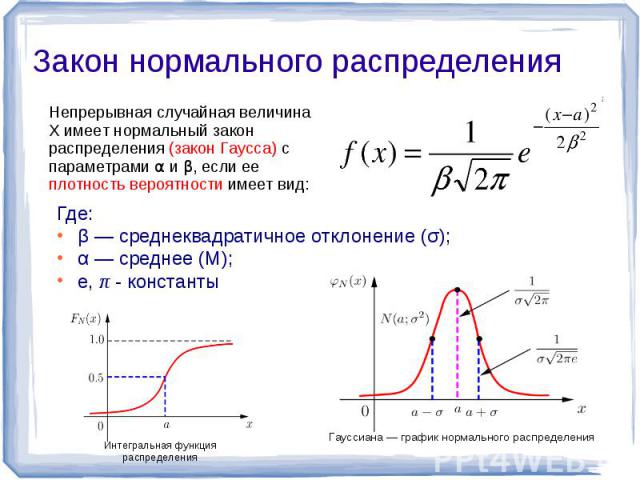
Закон нормального распределения Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами α и β, если ее плотность вероятности имеет вид: Где:β — среднеквадратичное отклонение (σ);α — среднее (М);e, π - константы

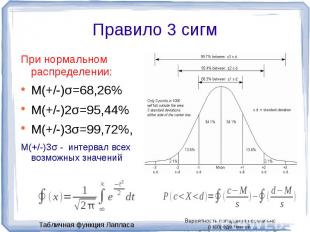
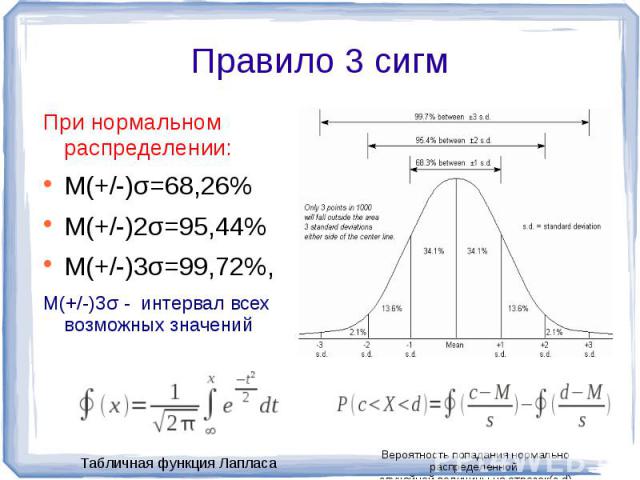
При нормальном распределении:M(+/-)σ=68,26%M(+/-)2σ=95,44%M(+/-)3σ=99,72%,M(+/-)3σ - интервал всех возможных значений Вероятность попадания нормально распределенной случайной величины на отрезок(с,d)

Свойства нормального распределения Правило 3 сигм (99,72% значений лежат в рамках M+/-3σ)Распределение симметрично (А=0), эксцесс, т.е. мера остроты пика или Е = 0Мода, медиана и среднее совпадаютЗначения, лежащие на равном расстоянии от M (среднего), будут иметь равную частоту в репрезентативной выборке

Проверка распределения на «нормальность» Графический способ;Статистический критерий Колмогорова-Смирнова (N>50 человек) ;W-критерий Шапиро-Уилка (N > 8 человек);Критерий ассиметрии и эксцессаСм. ГОСТ Р ИСО 5479—2002

1. Определить среднее арифметическое (М) и стандартное отклонение (σ).2. Рассчитать показатели асимметрии и эксцесса.А= Е= -33. Рассчитать критические значения А и ЕА Е4. Если А<Aкр и E<Eкр, распределение нормально

Знаем, какой процент испытуемых наберет определенные баллы по тесту;Стандартизируем на этой основе баллы по тесту;Оцениваем параметры генеральной совокупности по выборочным данным;Рассчитываем статистическую значимость наших выводов;И задействуем его во всей индуктивной статистике в той или иной степени...