Презентация на тему: Определение синуса, косинуса, тангенса и котангенса

Тема: Определение синуса, косинуса, тангенса и котангенса.

Цели урока: 1.Знать определение синуса, косинуса, тангенса и котангенса.2.Уметь применять эти определения к решению примеров и задач.3.Привитие творческой активности и самостоятель-ности

План урока История развития тригонометрии.Повторение курса геометрии.Изучение нового материала.Закрепление

Историческая справка тригононТригонометрия метрио (измерение треугольника)

Древний Вавилон-умели предсказывать солнечные и лунные затмения.Древнегреческие учёные-составили таблицы хорд(первые тригонометрические таблицы)Учёные Индии и Ближнего Востока-положили начало радианной мере угла.

ГиппархПтолемейФрансуа ВиетЭйлерБернулли Большой вклад в развитие тригонометрии внесли:

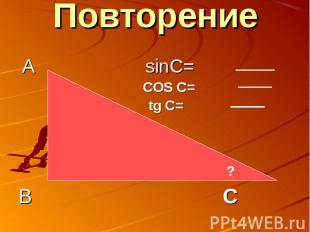
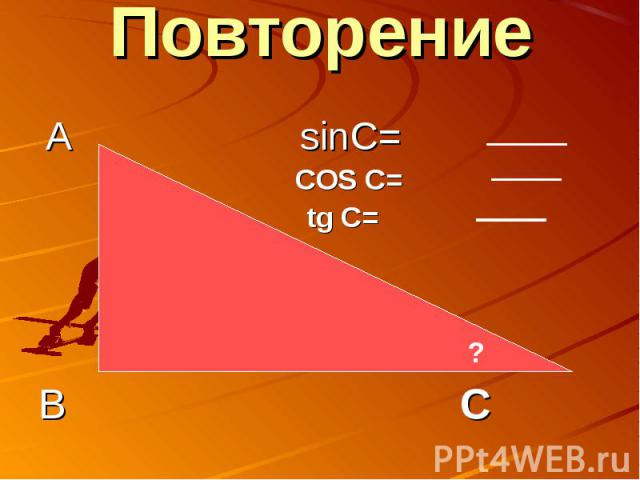
Повторение А sinC= COS C= tg C=В С

Повторение Для единичной полуокружности y у SIN A = = Y R X COS A= = X R 0 ≤SIN A≤ 1 -1 ≤ COS A ≤1 х

Повторение Основное тригонометрическое тождество:SIN2 X+COS2 Х=1

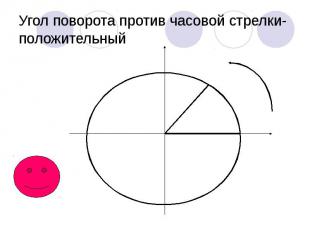
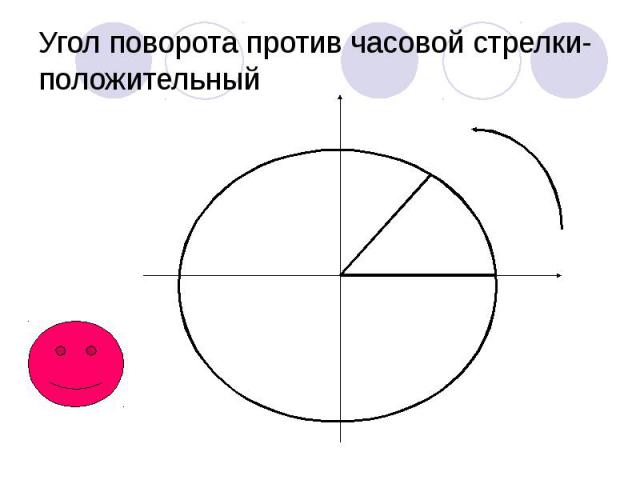
Угол поворота против часовой стрелки- положительный

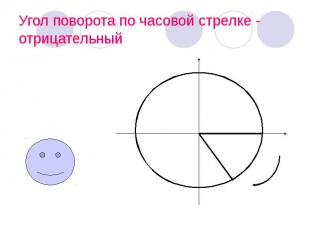
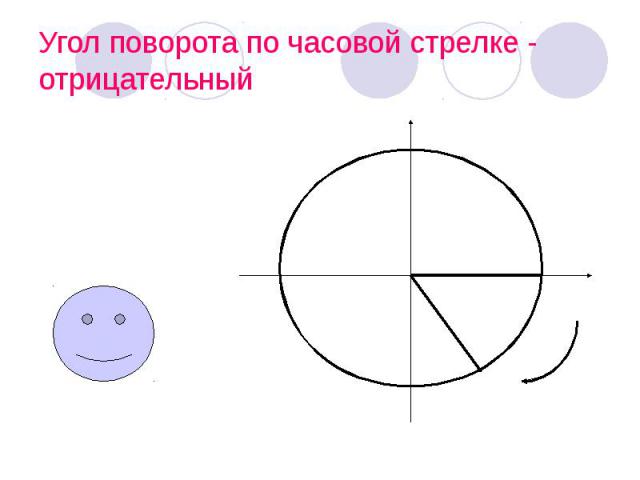
Угол поворота по часовой стрелке - отрицательный

Угол поворота Положительный Отрицательный

Из курса геометрии известно: Мера угла в градусах выражается числом от 00 до 1800

Каким числом может выражаться в градусах угол поворота?

В Ы В О Д:Угол поворота может выражаться в градусах каким угодно действительным числом от -∞ до +∞

Рассмотрим примеры 1350+3600n , n=0,1,-1,2,-2…..

В Ы В О ДСуществует бесконечно много углов поворота, при которых начальный радиус ОА переходит в радиус ОВ. В зависимости от того, в какой координатной четверти окажется радиус ОВ, угол α называют углом этой четверти.

З А П О М Н И 00

В ы в о д:Эти углы не относятся ни к какой четверти. 00 ,± 900 ,± 1800 , ± 2700 ,± 3600....

Углом какой четверти является угол β,если: β=1670 β=2870 β=-650

Стр.153.- определение. y XSinα= Cos= R R y X tgα= ctgα= X y

Лабораторная работа

В Ы В О Д: Синус, косинус, тангенс и котангенс не зависят от радиуса. Вычертите три окружности произвольного радиуса с центром в начале координат.Постройте начальный радиус ОА.Поверните начальный радиус на угол α=450В каждом из случаев найдите SIN 450.(смотри пример 1. стр.154.)Какой получился результат? Сделай вывод..

Запомни Sinα, Cosα-определены при любом α. Почему?

При каком α tgα не определён?Почему?

sinα , cosα , tgα , ctgα –называют тригонометрическими функциями.

Область значения синуса и косинуса есть промежуток [-1;1]Область значения тангенса и котангенса есть множество всех действительных чисел.

Найти синус, косинус,тангенс и котангенс 2700Проверьте решение на стр.156

Устно № 699№701

Письменно №705Используй таблицу стр.155