Презентация на тему: Вписанный угол

Вписанный угол
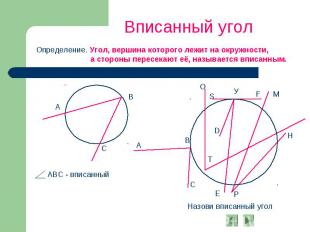
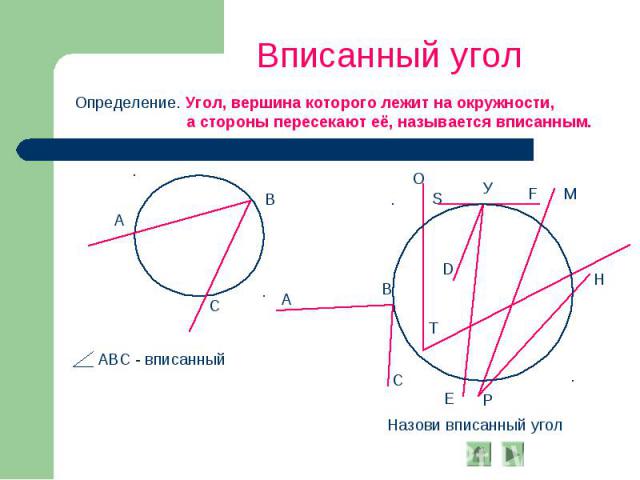
Вписанный угол Определение. Угол, вершина которого лежит на окружности, а стороны пересекают её, называется вписанным. АВС - вписанный Назови вписанный угол

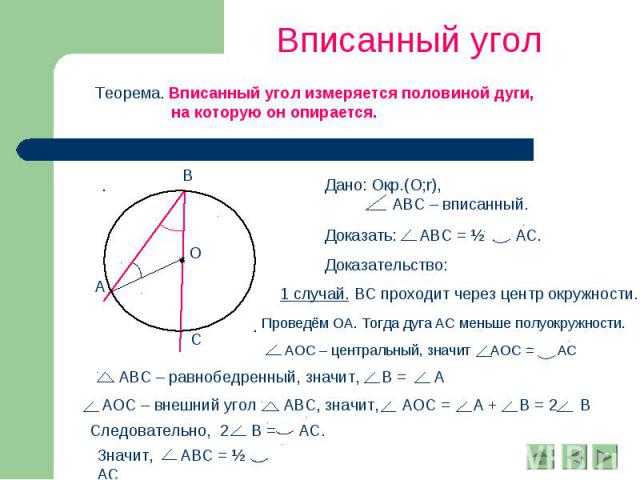
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Дано: Окр.(О;r), АВС – вписанный. Доказательство: 1 случай. ВС проходит через центр окружности. Проведём ОА. Тогда дуга АС меньше полуокружности. АОС – центральный, значит АОС = АС АВС – равнобедренный, значит, В = А АОС – внешний угол АВС, значит, АОС = А + В = 2 В Следовательно, 2 В = АС. Значит, АВС = ½ АС

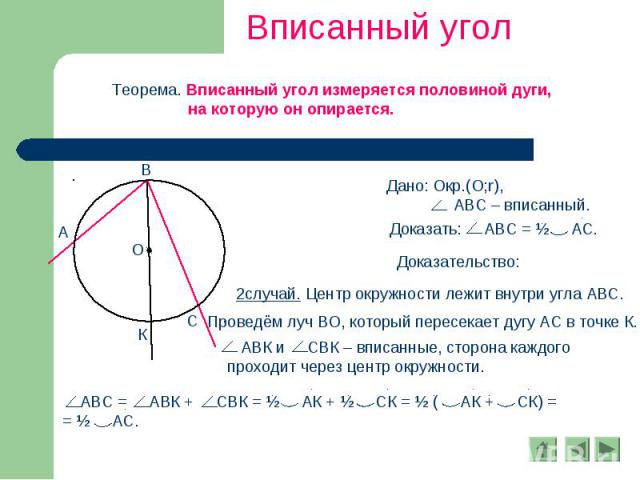
Вписанный угол Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Дано: Окр.(О;r), АВС – вписанный. 2случай. Центр окружности лежит внутри угла АВС. Проведём луч ВО, который пересекает дугу АС в точке К. АВК и СВК – вписанные, сторона каждого проходит через центр окружности. АВС = АВК + СВК = ½ АК + ½ СК = ½ ( АК + СК) == ½ АС.

Теорема. Вписанный угол измеряется половиной дуги, на которую он опирается. Дано: Окр.(О;r), АВС - вписанный. Доказать: АВС = ½ АС. Доказательство: 3 случай. Центр окружности лежит вне угла АВС. АВК и СВК – вписанные, сторона каждого проходит через центр окружности. АВС = АВК - СВК = ½ АК - ½ СК = ½ ( АК - СК) == ½ АС.
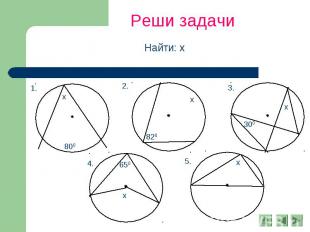
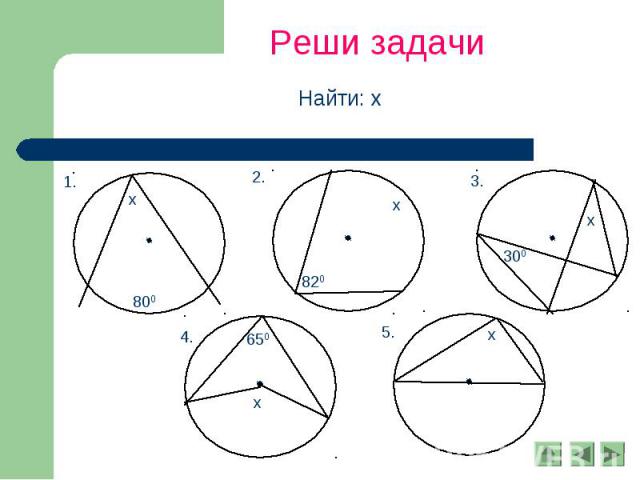
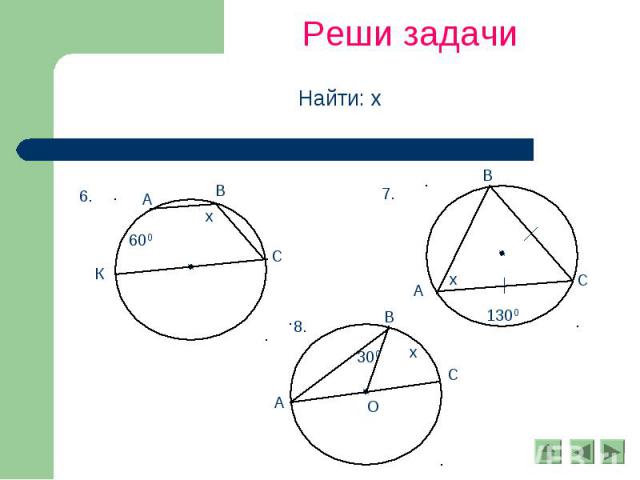
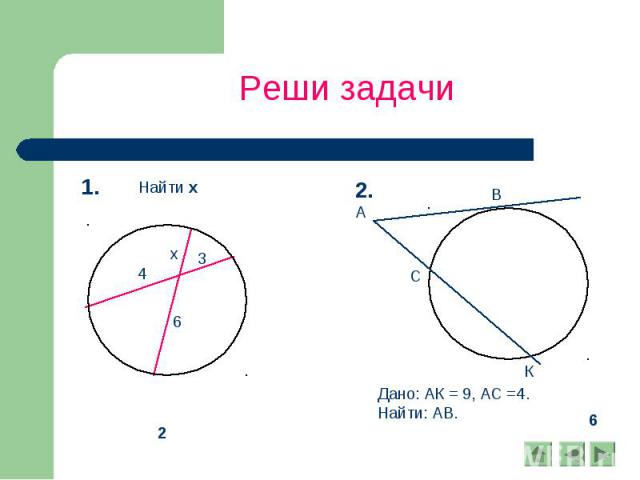
Реши задачи Найти: х
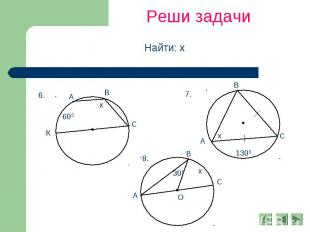
Реши задачи
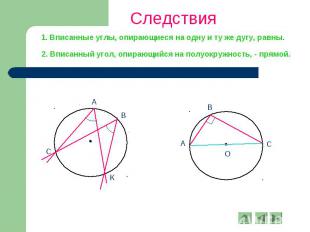
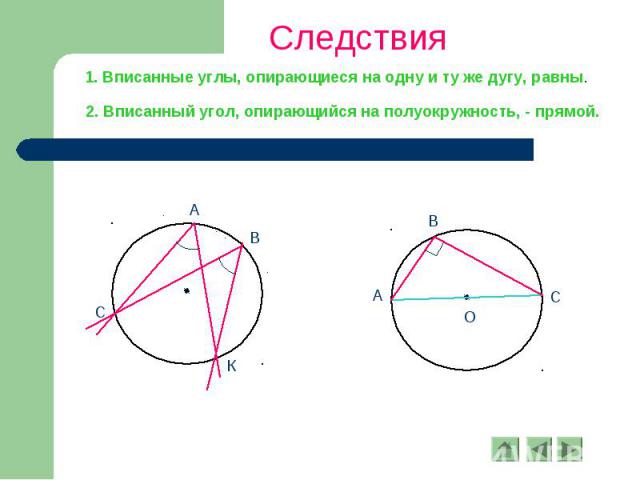
Следствия 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны. 2. Вписанный угол, опирающийся на полуокружность, - прямой.
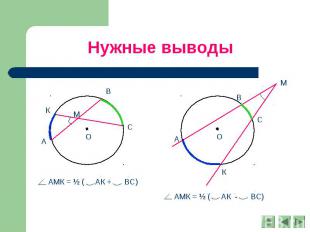
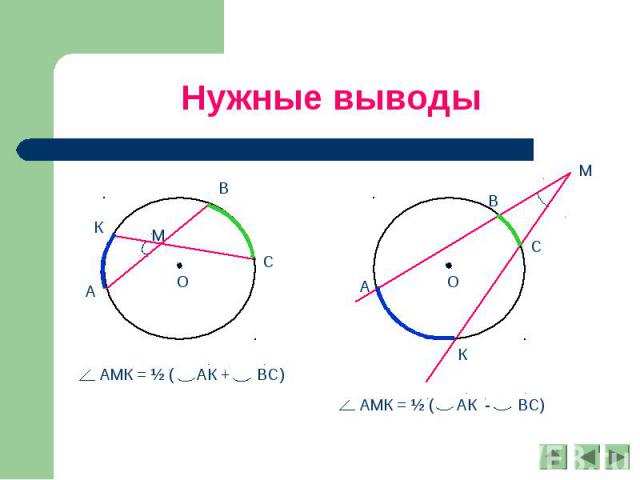
Нужные выводы АМК = ½ ( АК + ВС) АМК = ½ ( АК - ВС)
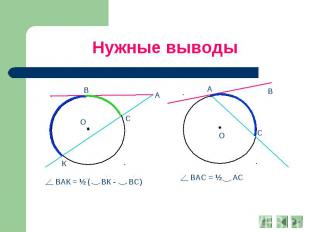
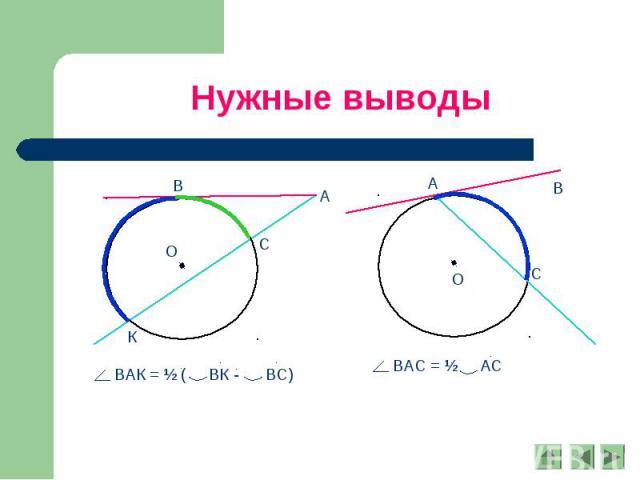
Нужные выводы ВАК = ½ ( ВК - ВС) ВАС = ½ АС

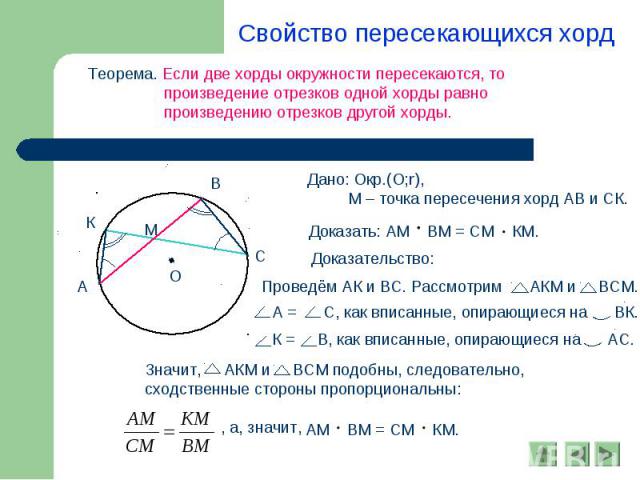
Теорема. Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. Дано: Окр.(О;r), М – точка пересечения хорд АВ и СК. Доказательство: А = С, как вписанные, опирающиеся на ВК. К = В, как вписанные, опирающиеся на АС. Значит, АКМ и ВСМ подобны, следовательно, сходственные стороны пропорциональны:
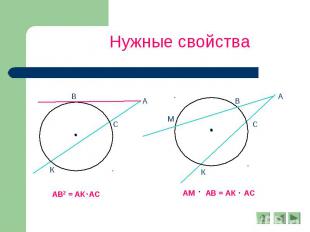
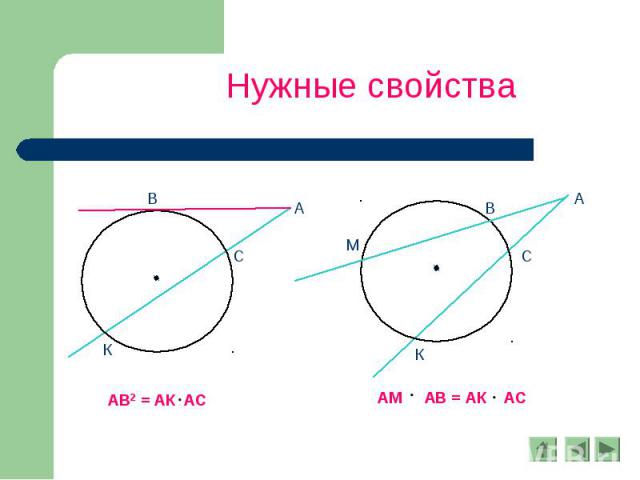
Нужные свойства АВ2 = АК АС АМ АВ = АК АС
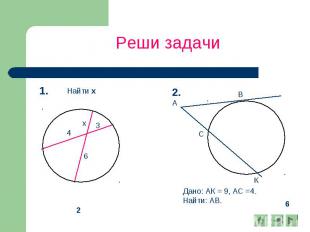
Реши задачи Дано: АК = 9, АС =4.Найти: АВ.

Желаю успехов в учёбе Михайлова Л. П.ГОУ ЦО № 173.