Презентация на тему: Вписанная окружность

Вписанная окружность

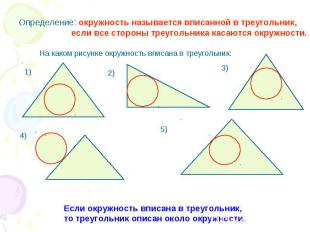
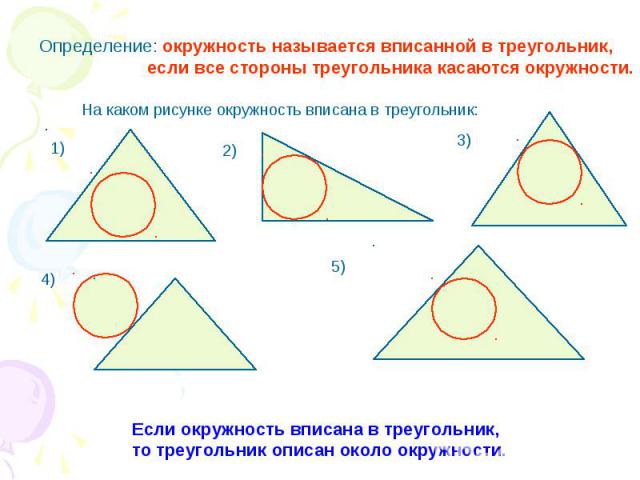
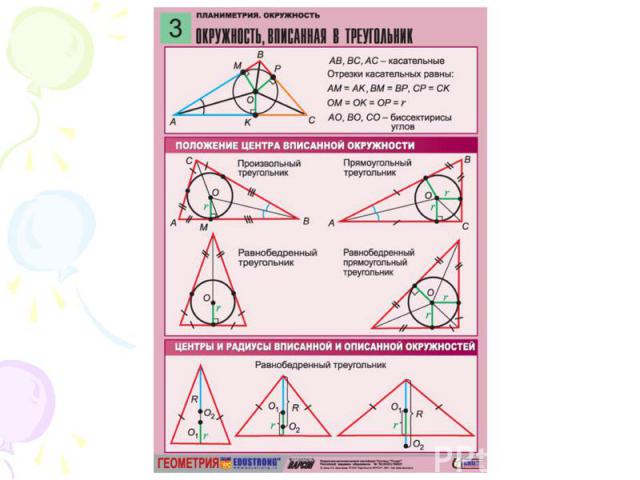
Определение: окружность называется вписанной в треугольник, если все стороны треугольника касаются окружности. На каком рисунке окружность вписана в треугольник: Если окружность вписана в треугольник, то треугольник описан около окружности.

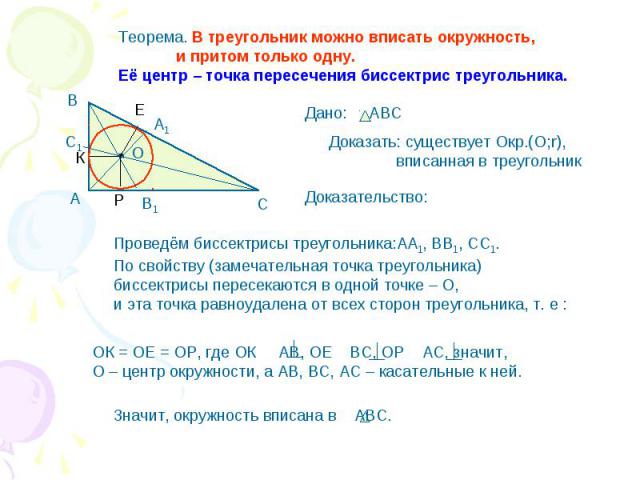
Теорема. В треугольник можно вписать окружность, и притом только одну.Её центр – точка пересечения биссектрис треугольника. Доказать: существует Окр.(О;r), вписанная в треугольник Проведём биссектрисы треугольника:АА1, ВВ1, СС1. По свойству (замечательная точка треугольника)биссектрисы пересекаются в одной точке – О, и эта точка равноудалена от всех сторон треугольника, т. е : ОК = ОЕ = ОР, где ОК АВ, ОЕ ВС, ОР АС, значит, О – центр окружности, а АВ, ВС, АС – касательные к ней.Значит, окружность вписана в АВС.

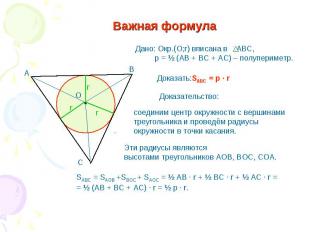
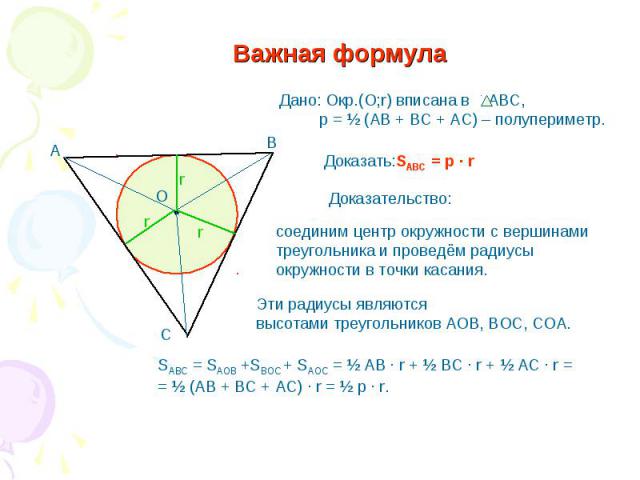
Важная формула Дано: Окр.(О;r) вписана в АВС, р = ½ (АВ + ВС + АС) – полупериметр. Доказательство: соединим центр окружности с вершинами треугольника и проведём радиусы окружности в точки касания. Эти радиусы являются высотами треугольников АОВ, ВОС, СОА. SABC = SAOB +SBOC + SAOC = ½ AB · r + ½ BC · r + ½ AC · r == ½ (AB + BC + AC) · r = ½ p · r.

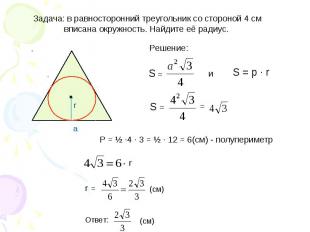
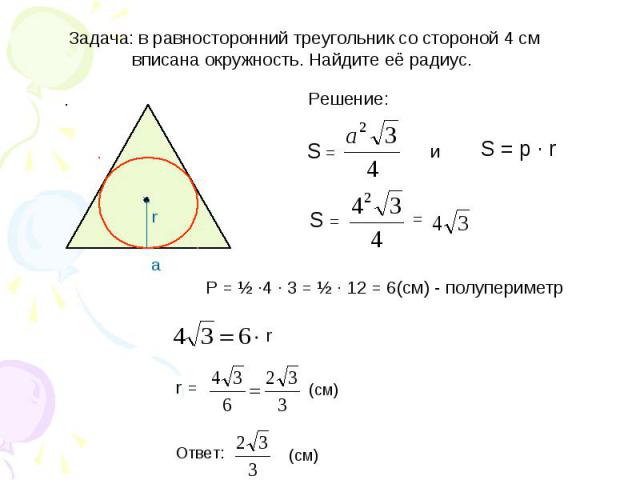
Задача: в равносторонний треугольник со стороной 4 см вписана окружность. Найдите её радиус. P = ½ ·4 · 3 = ½ · 12 = 6(см) - полупериметр

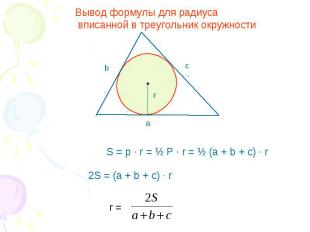
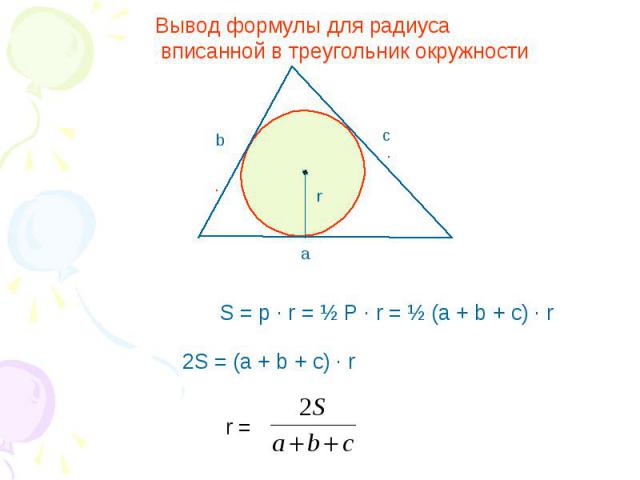
Вывод формулы для радиуса вписанной в треугольник окружности S = p · r = ½ P · r = ½ (a + b + c) · r 2S = (a + b + c) · r

Задача: в прямоугольный треугольник вписана окружность, гипотенуза точкой касания делится на отрезки 6 см и 4 см. Найдите радиус вписанной окружности. Дано: АВС, С = 900 Окр.(О;r) вписана, АМ = 6 см, ВМ = 4 смНайти: r. Т. к. Окр.(O;r) вписана в АВС, тоАВ, АС,ВС – касательные и по свойству касательных, проведённых из одной точки:АМ = АК = 6 см, ВЕ = ВМ = 4 см, СК = СЕ Т. к. С = 900, то СКОЕ – квадрат, поэтому СК = СЕ = r. По теореме Пифагора: АС2 + ВС2 = АВ2 (6 + r)2 + (4 + r)2 = 102 Решив квадратное уравнение, получим r = 2 см

Нужная формула для радиуса окружности, вписанной в прямоугольный треугольник Т. к. Окр.(О;r) вписана в треугольник АВС, у которого угол С – прямой, то АС, ВС, АВ – касательные и СКОЕ – квадрат, значит, СК = СЕ = r АК = АМ = b - r AB = AM + BM c = b – r + a - r 2r = a + b - c r = ½ (a + b – c)

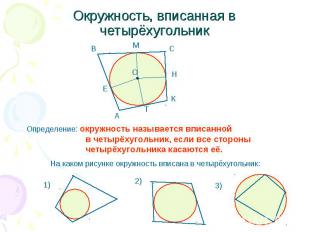
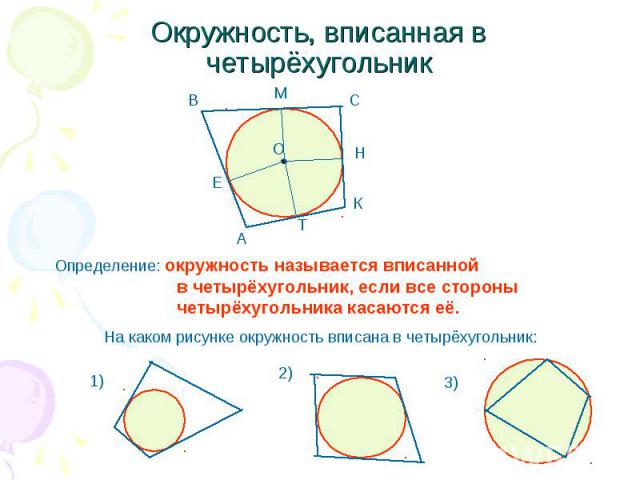
Окружность, вписанная в четырёхугольник Определение: окружность называется вписанной в четырёхугольник, если все стороны четырёхугольника касаются её. На каком рисунке окружность вписана в четырёхугольник:

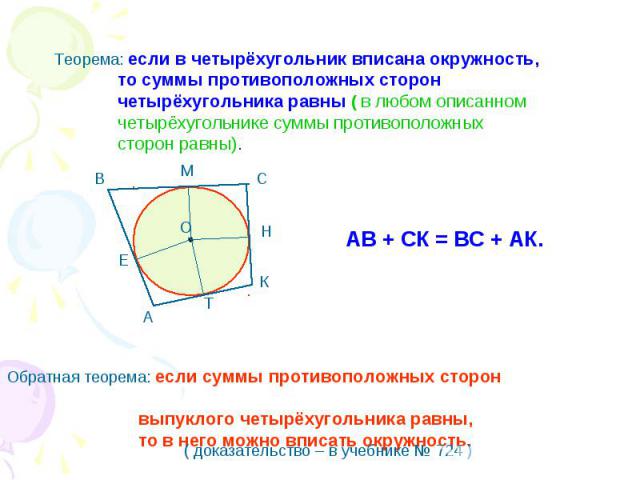
Теорема: если в четырёхугольник вписана окружность, то суммы противоположных сторон четырёхугольника равны ( в любом описанном четырёхугольнике суммы противоположных сторон равны). АВ + СК = ВС + АК. Обратная теорема: если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

Задача: в ромб, острый угол которого 600, вписана окружность, радиус которой равен 2 см. Найти периметр ромба. Дано: Окр.(О; 2 см) вписана в ромб FSLZ, F = 600. Найти: РFSLZ Т. к. окружность вписана в ромб, то стороны ромба касаются окружности, значит, АВ FZ, AB = 2r = 4см – диаметр. Проведём SC FZ, SC = AB (как перпендикуляры междупараллельными прямыми), SC = 4см FSC – прямоугольный,

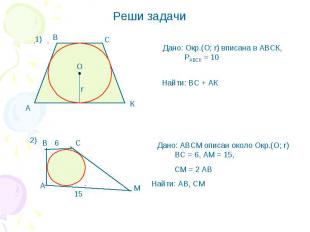
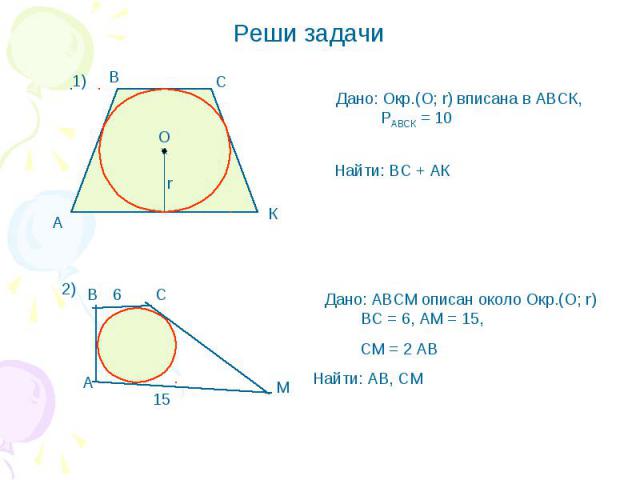
Дано: Окр.(О; r) вписана в АВСК, РАВСК = 10 Найти: ВС + АК Дано: АВСМ описан около Окр.(О; r) BC = 6, AM = 15, СМ = 2 АВ Найти: АВ, СМ