Презентация на тему: Вневписанная окружность

Вневписанная окружность Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать.Г. Галилей

Вневписанная окружность Простейший из многоугольников — треугольник — играет в геометрии особую роль. За несколько тысячелетий геометры столь подробно изучили треугольник, что иногда говорят о «геометрии треугольника» как о самостоятельном разделе элементарной геометрии.Первые упоминания о треугольнике и его свойствах можно найти в египетских папирусах, которым более 4000 лет. Через 2000 лет в Древней Греции изучение свойств треугольника достигает высокого уровня — достаточно вспомнить теорему Пифагора и формулу Герона.Центральное место в геометрии треугольника занимают свойства так называемых замечательных точек и линий.

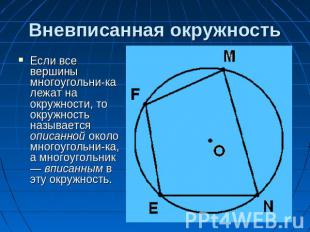
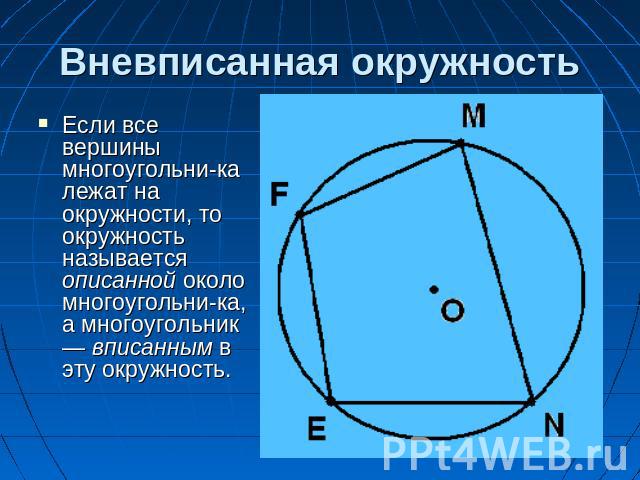
Вневписанная окружность Если все вершины многоугольни-ка лежат на окружности, то окружность называется описанной около многоугольни-ка, а многоугольник — вписанным в эту окружность.

Вневписанная окружность Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.

Вневписанная окружностьТри серединных перпендикуля-ра к сторонам треугольника пересекаются в одной точке — центре описанной около треугольника окружности.

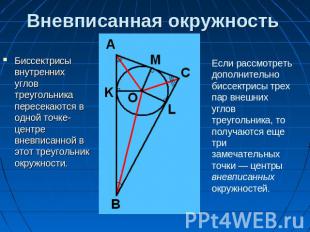
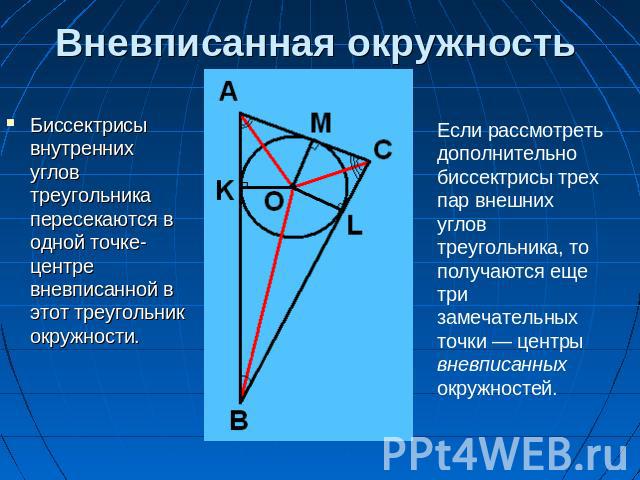
Вневписанная окружность Биссектрисы внутренних углов треугольника пересекаются в одной точке- центре вневписанной в этот треугольник окружности. Если рассмотреть дополнительно биссектрисы трех пар внешних углов треугольника, то получаются еще три замечательных точки — центры вневписанных окружностей.

Вневписанная окружность Биссектрисы внешних или внутренних углов треугольника образуют центры окружностей касающихся прямых АВ, ВС, СА.

Вневписанная окружность В итоге получаем четыре окружности с центрами О, Оа, Ob, Oc, касающиеся трех данных несовпадающих прямых. При этом одна из них будет вписанной в треугольник окружностью, а три других — вневписанными окружностями.

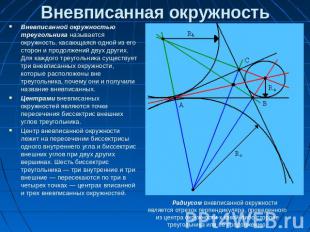
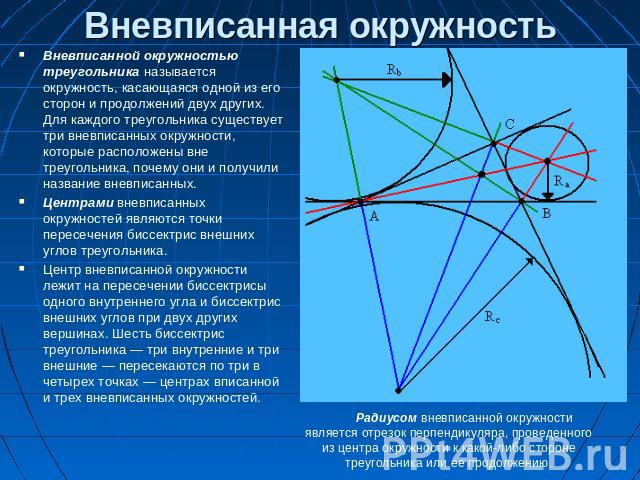
Вневписанная окружность Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других. Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, почему они и получили название вневписанных.Центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.Центр вневписанной окружности лежит на пересечении биссектрисы одного внутреннего угла и биссектрис внешних углов при двух других вершинах. Шесть биссектрис треугольника — три внутренние и три внешние — пересекаются по три в четырех точках — центрах вписанной и трех вневписанных окружностей. Радиусом вневписанной окружности является отрезок перпендикуляра, проведенного из центра окружности к какой-либо стороне треугольника или ее продолжению.

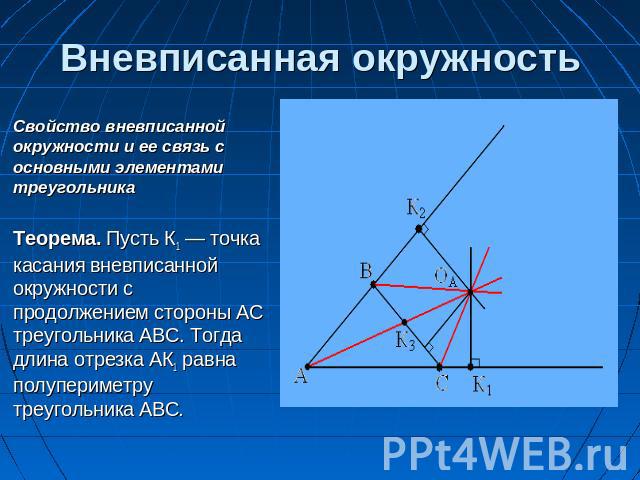
Вневписанная окружность Свойство вневписанной окружности и ее связь с основными элементами треугольникаТеорема. Пусть К1 — точка касания вневписанной окружности с продолжением стороны АС треугольника ABC. Тогда длина отрезка АК1 равна полупериметру треугольника ABC.

Вневписанная окружность Доказательство: 1). Пусть точки К2 и К3 — точки касания вневписанной окружности с прямыми АВ и ВС соответственно. 2). СК1 = СК3 ( по свойству ВК2 = ВК3 касательных к АК1 = АК2 окружности).3) Р = АС + СВ + АВ = = АС + СК3 + ВК3 + АВ = = АС + СК1 + ВК2 + АВ = = АК1 + АК2 = 2АК1Значит, АК1 = Р : 2Ч. т. д.

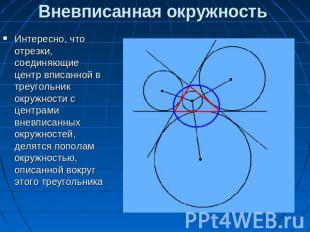
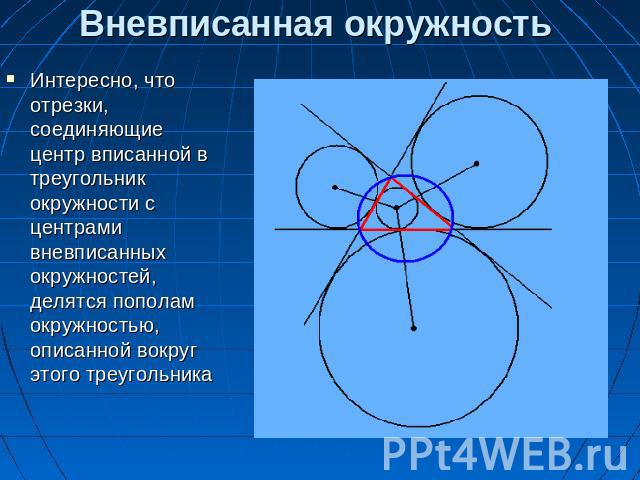
Вневписанная окружность Интересно, что отрезки, соединяющие центр вписанной в треугольник окружности с центрами вневписанных окружностей, делятся пополам окружностью, описанной вокруг этого треугольника

Всё!!!