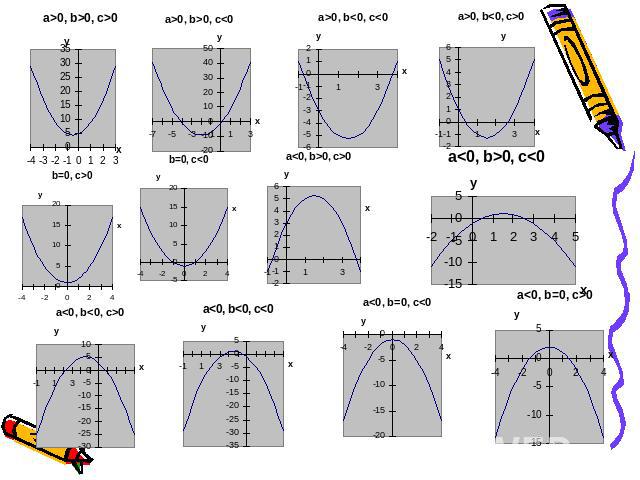
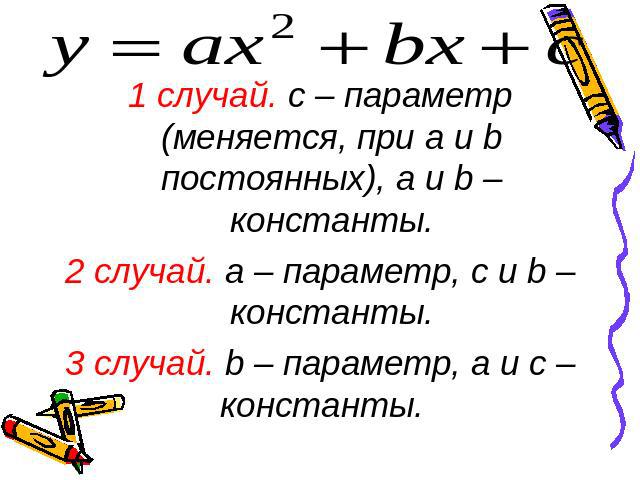Презентация на тему: Влияние коэффициентов на расположение параболы

Влияние коэффициентов на расположение параболы Выполнила: Дегтярева АнастасияУченица 10 классаМОУ «Тарская СОШ №4»Руководитель: ИвановаСветлана ЕвгеньевнаУчитель математикиМОУ «Тарская СОШ №4»

Цель: Исследовать зависимость свойств параболы от ее коэффициентов.

Задачи:Выяснить закономерность расположения вершин параболы.Рассмотреть некоторые параболы заданные квадратичной функцией.Выявить общие черты семейства парабол.

Объект: Парабола, как график квадратичной функции. Объект: Парабола, как график квадратичной функции. Предмет: зависимость расположения параболы от ее коэффициентов.
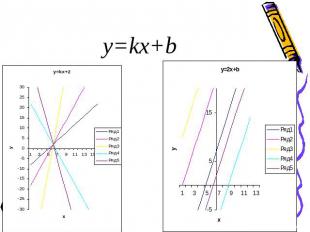
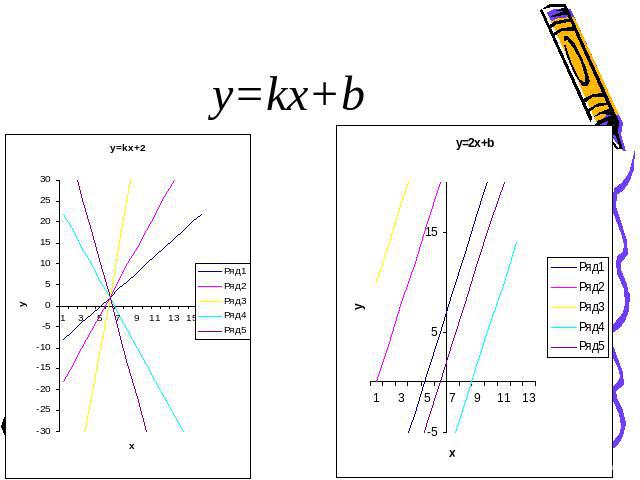
y=kx+b
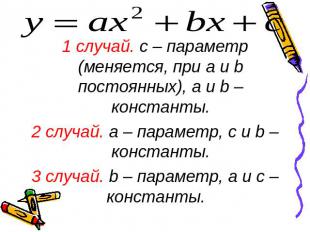
1 случай. с – параметр (меняется, при a и b постоянных), а и b – константы.2 случай. а – параметр, с и b – константы.3 случай. b – параметр, а и с – константы.
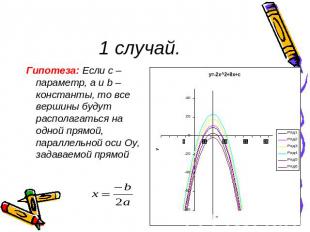
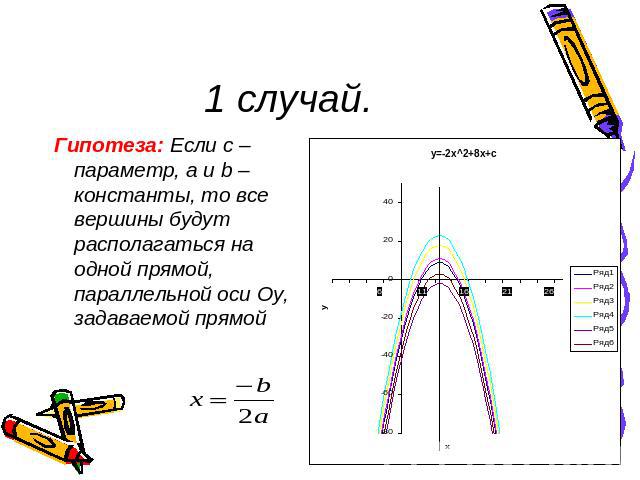
1 случай. Гипотеза: Если с – параметр, а и b – константы, то все вершины будут располагаться на одной прямой, параллельной оси Oy, задаваемой прямой
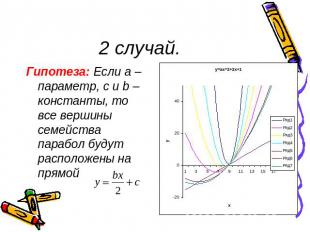
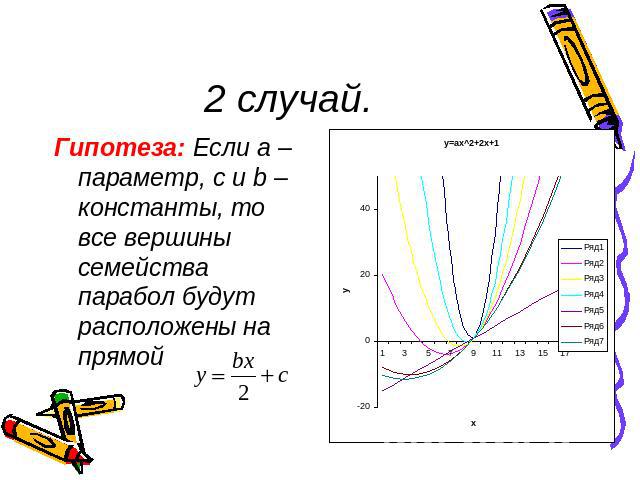
2 случай.Гипотеза: Если а – параметр, с и b – константы, то все вершины семейства парабол будут расположены на прямой
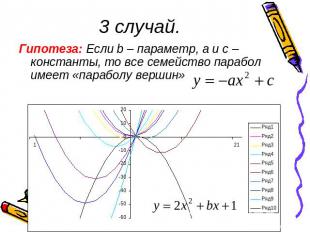
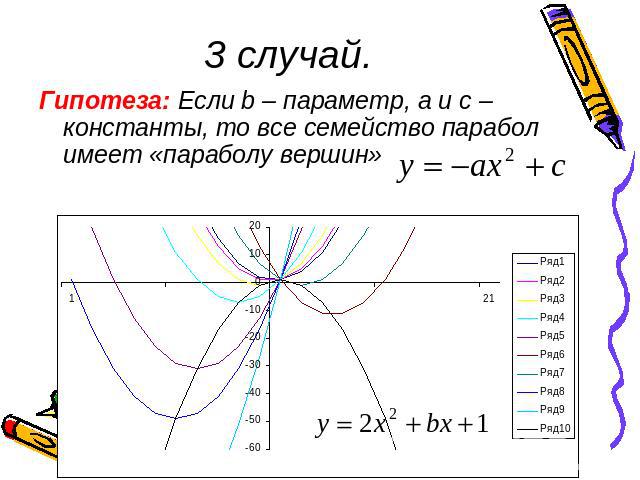
3 случай.Гипотеза: Если b – параметр, а и с – константы, то все семейство парабол имеет «параболу вершин»

Выводы: При изменении коэффициента с все вершины семейства парабол будут располагаться на одной прямой, параллельной оси Оу.При изменении коэффициента а все вершины семейства парабол будут располагаться на одной прямой.При изменения коэффициента b все вершины семейства парабол имеют общую «параболу вершин» и пересекаются в одной точке, в вершине «параболы вершин».