Презентация на тему: Вписанная окружность

Вписанная окружность Тема урока:

Цели урока: 1.Познакомится с определением вписанной окружности. 2.Изучить доказательство теоремы о вписанной окружности.3.Решение задач по данной теме.
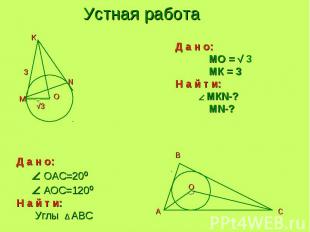
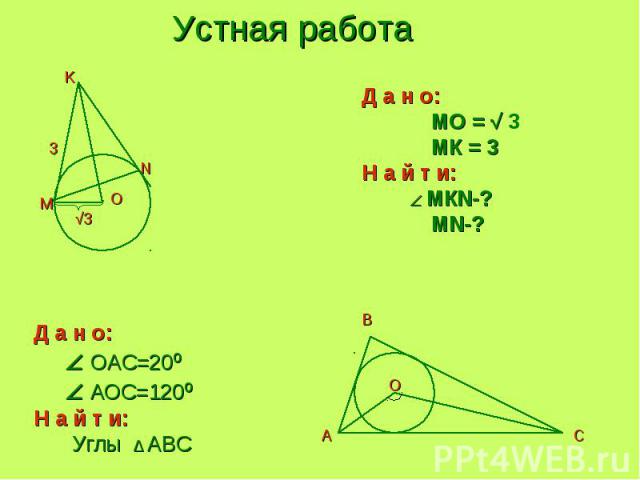
Устная работа Д а н о: MO = √ 3 МК = 3Н а й т и: МКN-? MN-? Д а н о: OAC=20º АOC=120ºН а й т и: Углы ∆ АBC

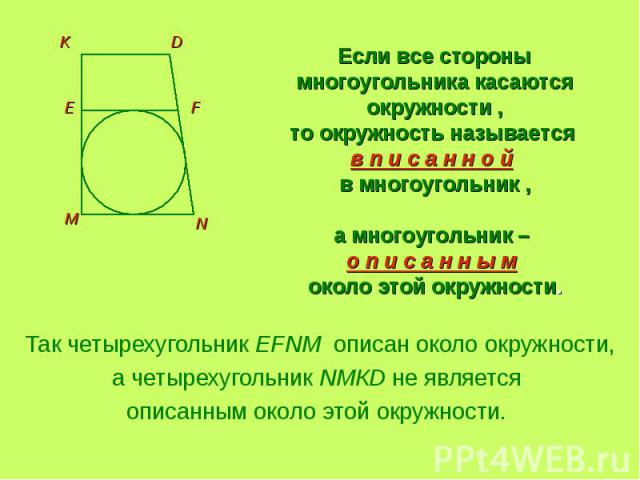
Если все стороны многоугольника касаются окружности ,то окружность называется в п и с а н н о й в многоугольник ,а многоугольник – о п и с а н н ы м около этой окружности. Так четырехугольник EFNM описан около окружности,а четырехугольник NMКD не является описанным около этой окружности.

Т е о р е м а В любой треугольник можно вписать окружность.
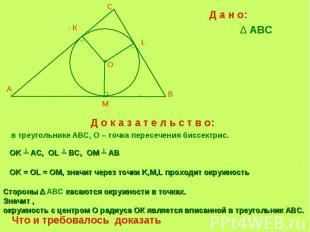
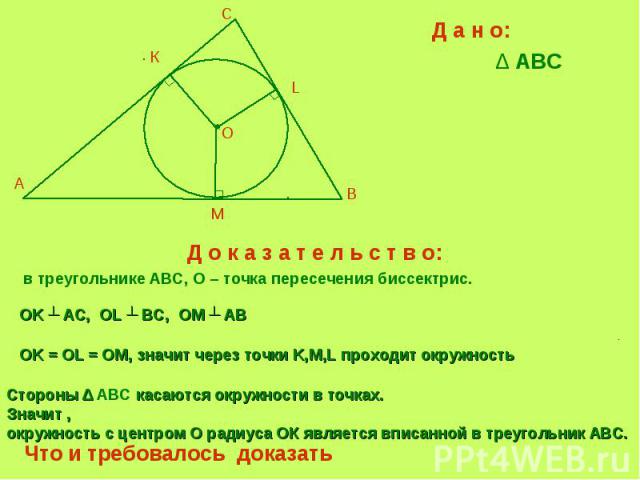
Д а н о:∆ ABC Д о к а з а т е л ь с т в о: в треугольнике ABC, О – точка пересечения биссектрис. OK ┴ AС, OL ┴ BC, OM ┴ AB OK = OL = OM, значит через точки K,M,L проходит окружность Стороны ∆ ABC касаются окружности в точках.Значит , окружность с центром О радиуса ОК является вписанной в треугольник АВС.
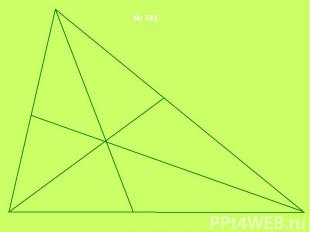

Домашняя работа : Пункт 74 (теорема) № 690 , №691 1. Что называется вписанной окружностью?2. Что является центром вписанной окружности?3. В любой ли треугольник можно вписать окружность?