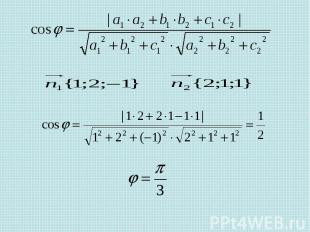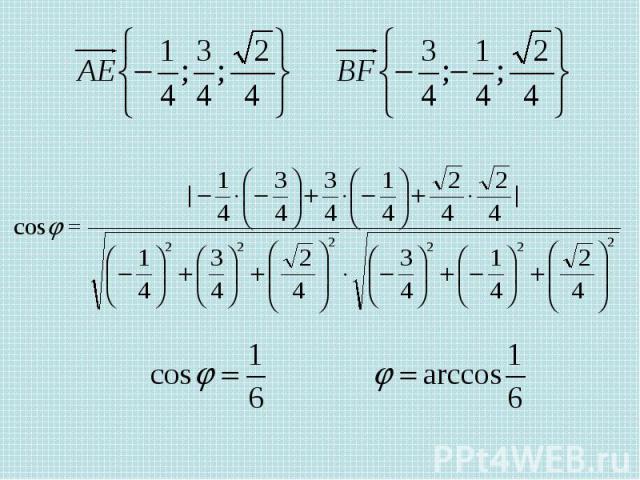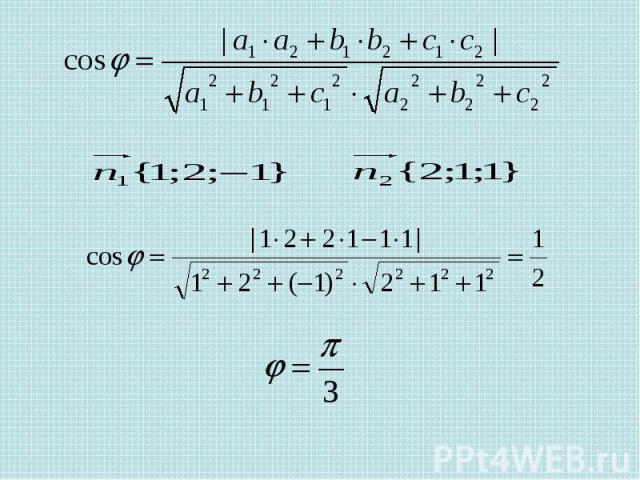Презентация на тему: Метод координат в задачах С2 Стереометрия

Метод координат в задачах С2 Стереометрия

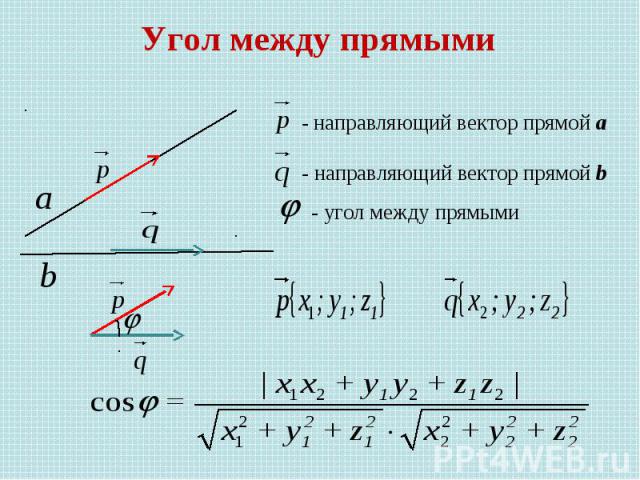
Угол между прямыми - направляющий вектор прямой а - направляющий вектор прямой b - угол между прямыми

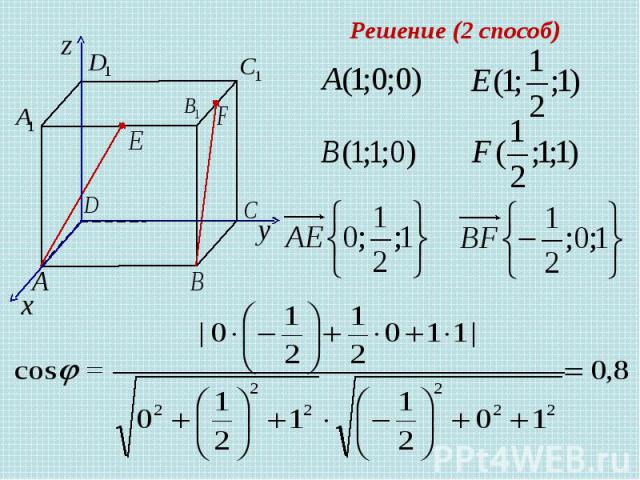
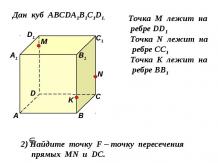
Задача 1 В единичном кубе найдите угол между прямыми AE и BF, где Е – середина ребра , а F – середина ребра К - середина Решение (1 способ) По теореме косинусов для
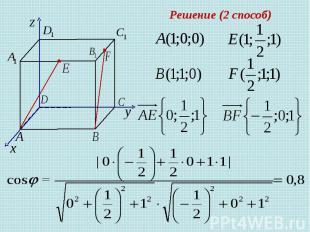
Решение (2 способ)

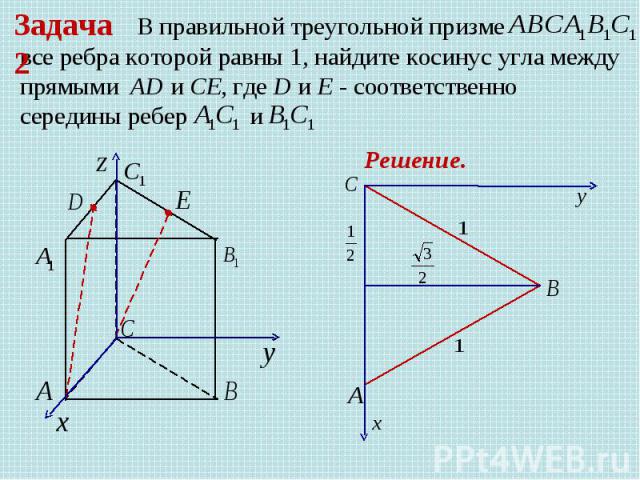
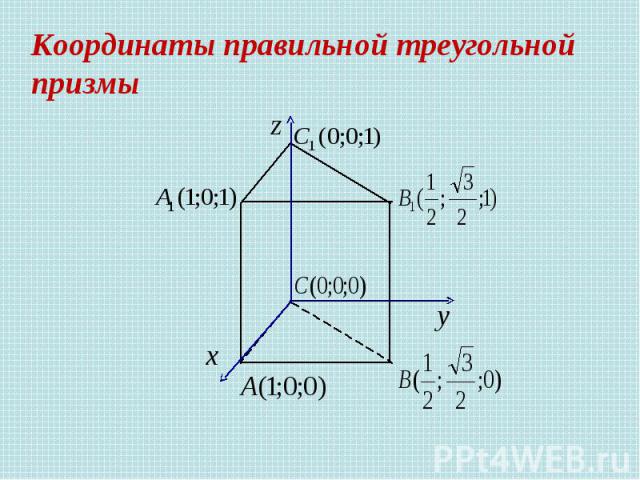
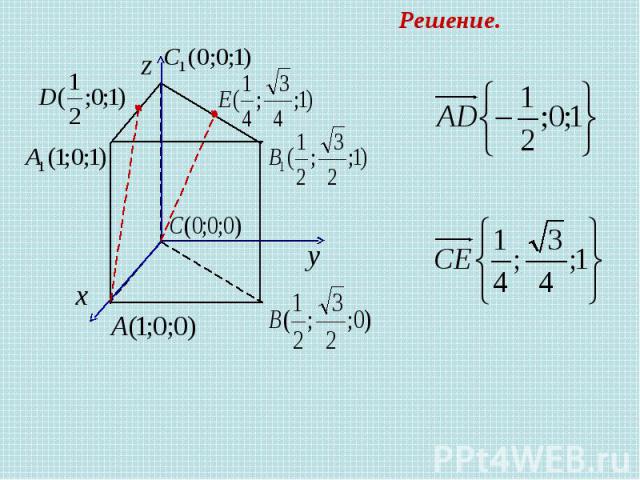
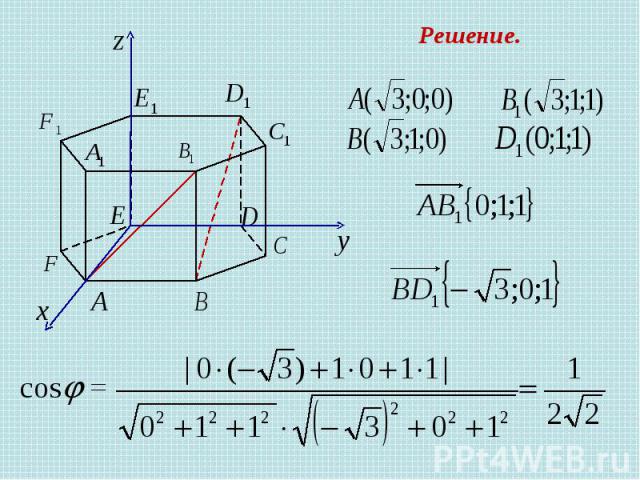
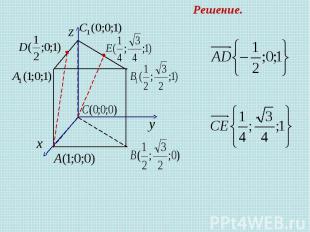
В правильной треугольной призме все ребра которой равны 1, найдите косинус угла между прямыми AD и CE, где D и E - соответственно середины ребер Задача 2 Решение.

Координаты правильной треугольной призмы
Решение

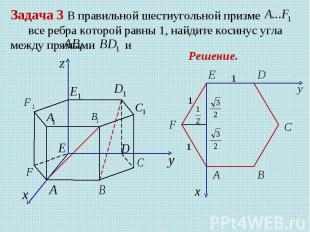
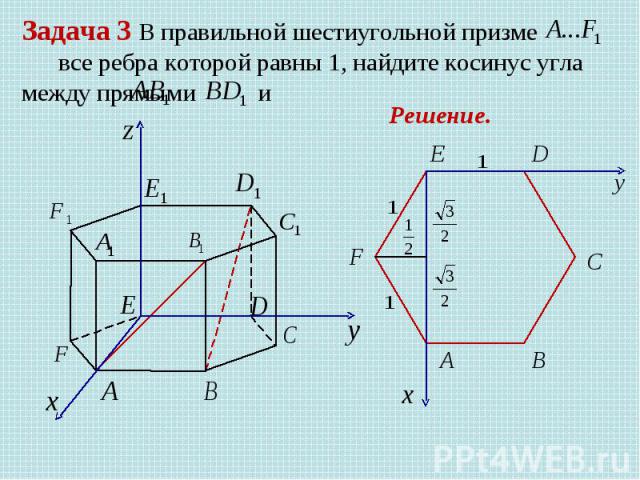
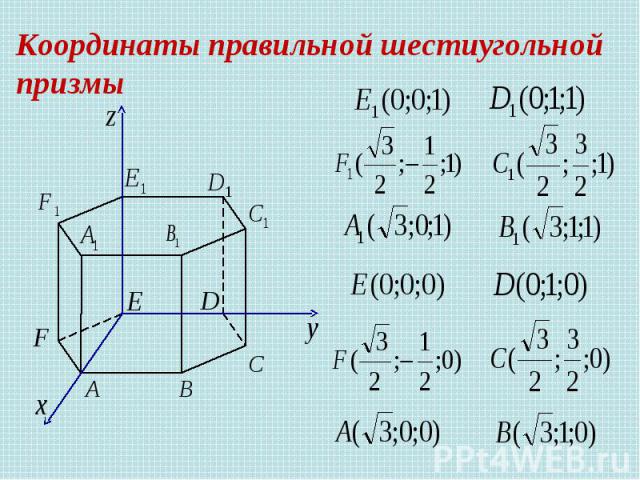
Задача 3 В правильной шестиугольной призме все ребра которой равны 1, найдите косинус угла между прямыми Решение.
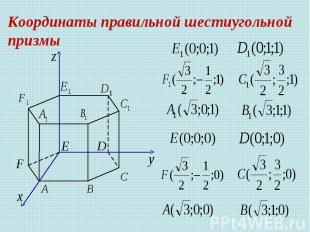
Координаты правильной шестиугольной призмы
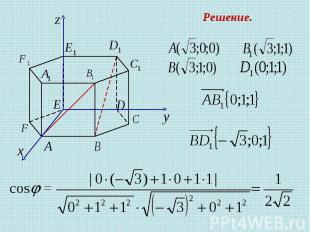
Решение.

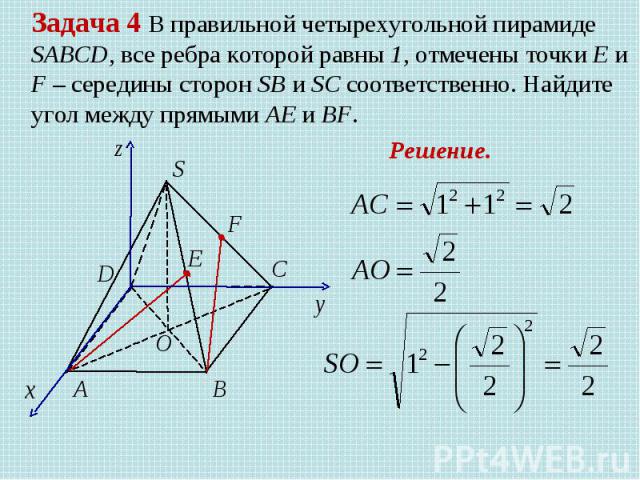
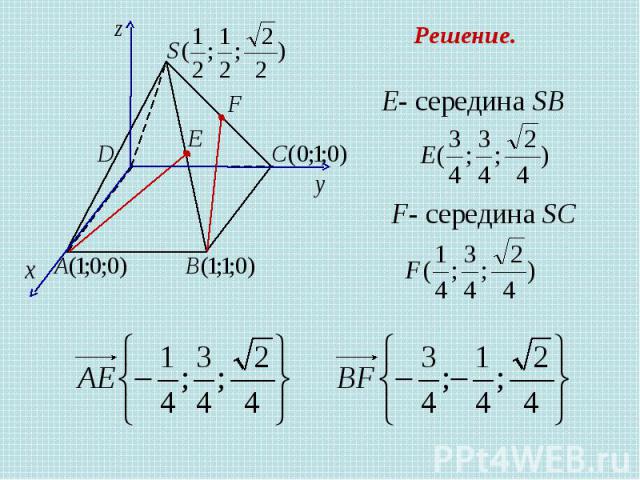
Задача 4 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки Е и F – середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF. Решение.

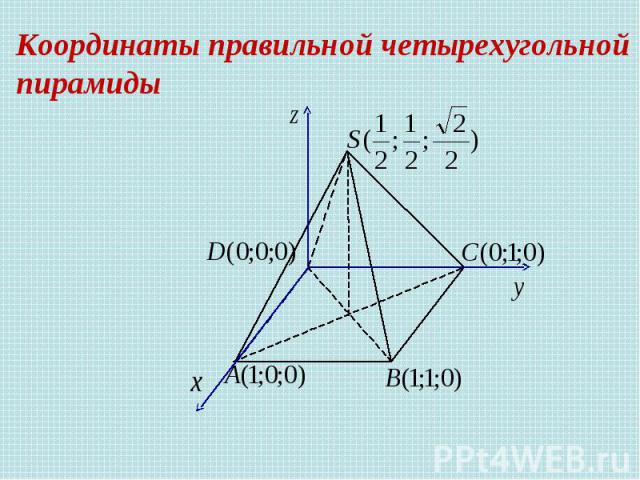
Координаты правильной четырехугольной пирамиды
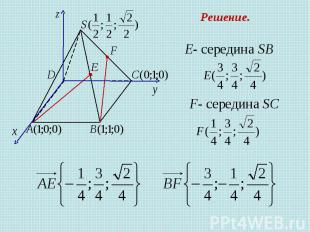
Е- середина SB F- середина SC Решение.


Угол между прямой и плоскостью - направляющий вектор прямой - нормальный вектор плоскости
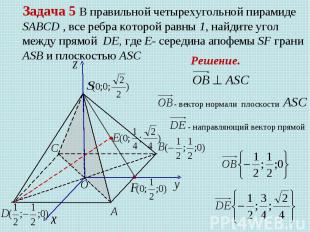
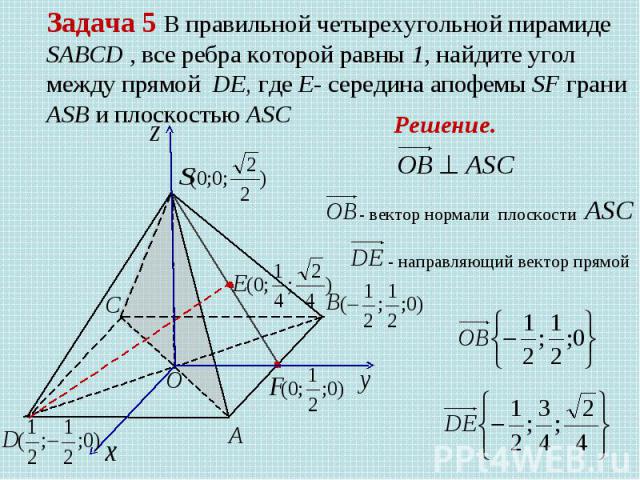
Задача 5 В правильной четырехугольной пирамиде SABCD , все ребра которой равны 1, найдите угол между прямой DE, где Е- середина апофемы SF грани ASB и плоскостью ASC Решение. - вектор нормали плоскости - направляющий вектор прямой

- вектор нормали плоскости - направляющий вектор прямой DE

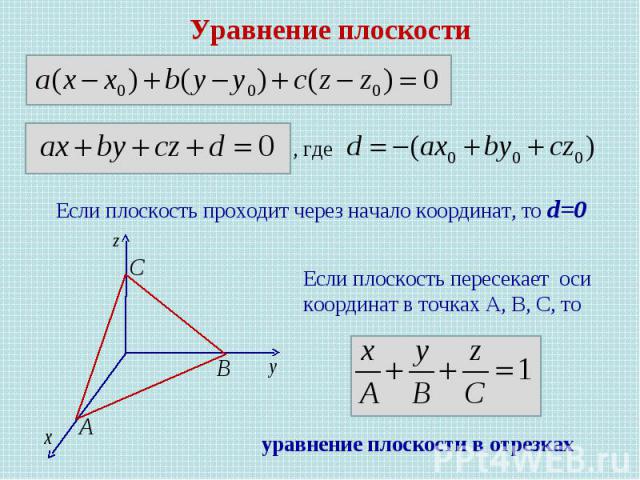
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору -нормальный вектор плоскости , где

Уравнение плоскости Если плоскость проходит через начало координат, то d=0 Если плоскость пересекает оси координат в точках А, В, С, то , где уравнение плоскости в отрезках

Задача 6 Составить уравнение плоскости, проходящей через точки А(-2;3;5), В(4;-3;0), С(0;6;-5) и найти координаты вектора нормали. Решение.

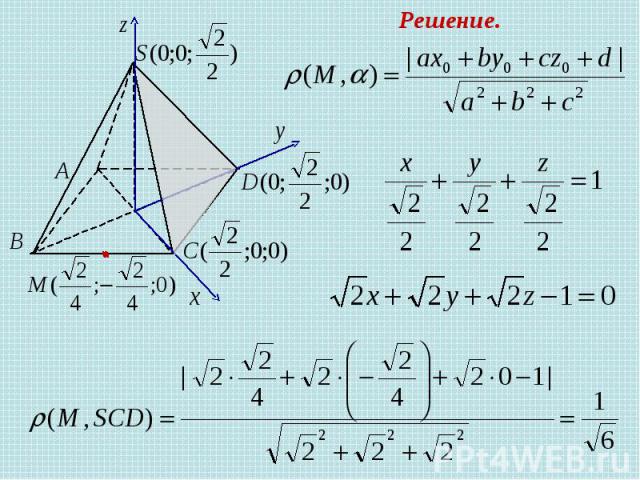
Расстояние от точки до плоскости

Расстояние между параллельными плоскостями
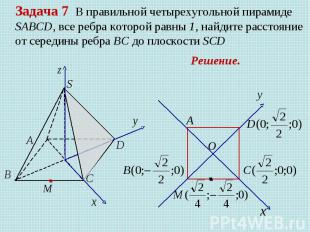
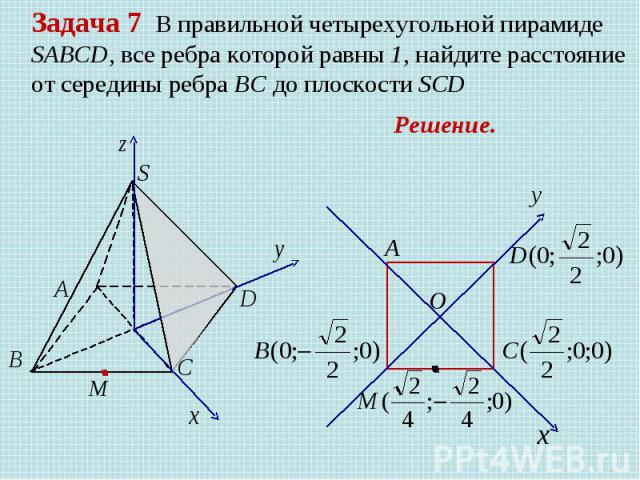
Задача 7 В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от середины ребра ВС до плоскости SCD Решение.
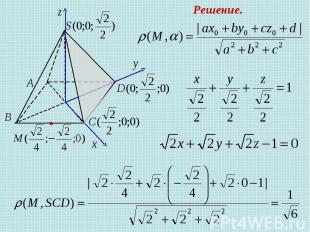
Решение.

Угол между плоскостями Вектор нормали плоскости Вектор нормали плоскости

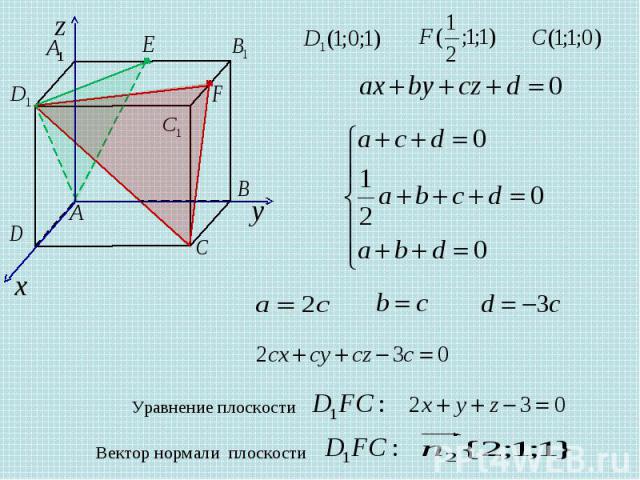
Задача 8 В единичном кубе найдите угол между плоскостями и , где Е – середина ребра , а F – середина ребра Решение. Уравнение плоскости Вектор нормали плоскости
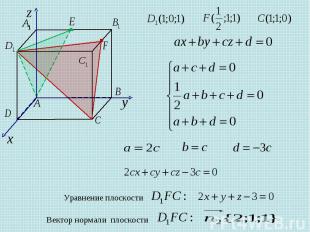
Уравнение плоскости Вектор нормали плоскости