Презентация на тему: Решение задач на комбинации многогранников и тел вращения

МОУ «Инсарская средняя общеобразовательная школа №1» Решение задач на комбинации многогранников и тел вращения Урок геометрии, 11 класс Чудаева Елена Владимировна, Республика Мордовия, г. Инсар
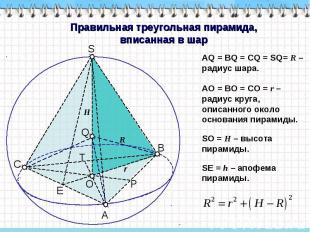
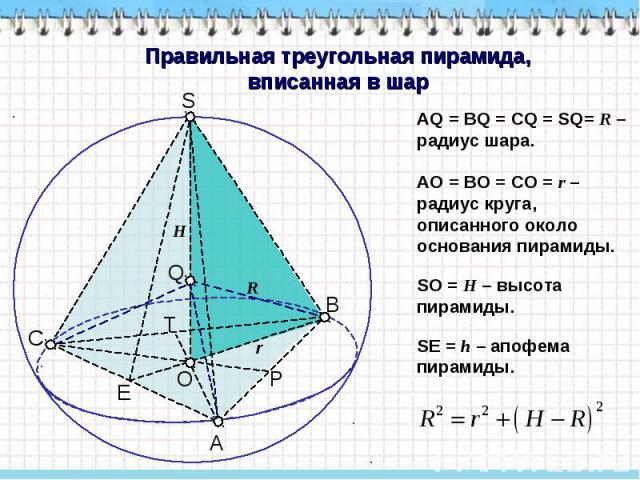
Правильная треугольная пирамида, вписанная в шар АQ = ВQ = CQ = SQ= R – радиус шара. AO = BO = CO = r – радиус круга, описанного около основания пирамиды. SO = H – высота пирамиды. SЕ = h – апофема пирамиды.
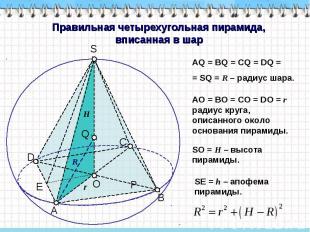
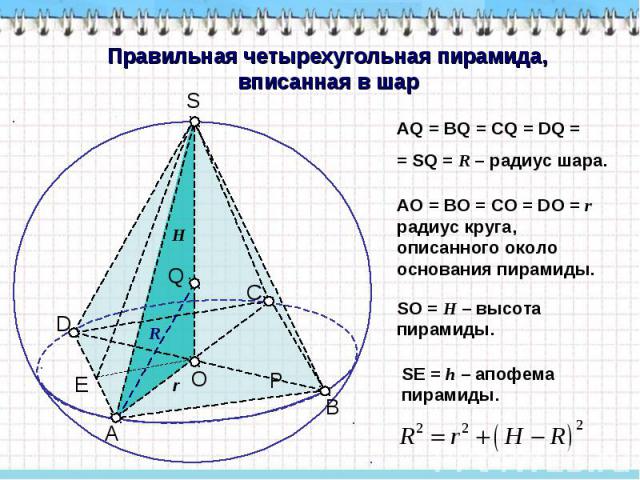
Правильная четырехугольная пирамида, вписанная в шар AQ = BQ = CQ = DQ = = SQ = R – радиус шара. AO = BO = CO = DO = r радиус круга, описанного около основания пирамиды. SO = H – высота пирамиды. SЕ = h – апофема пирамиды.
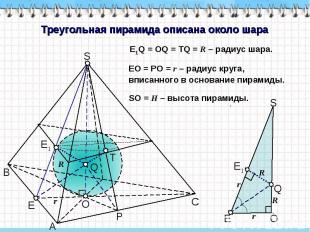
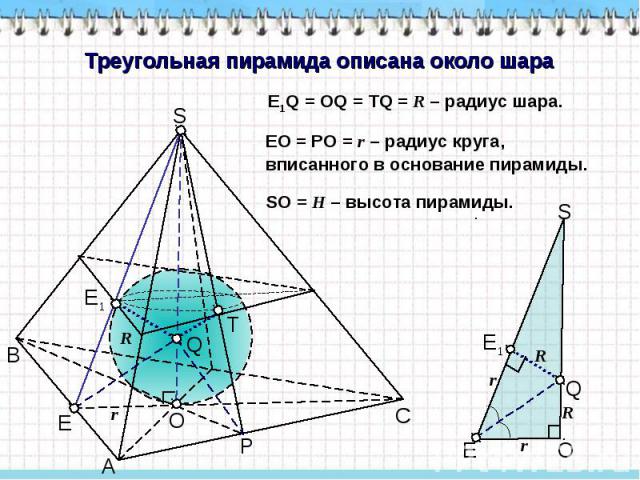
Треугольная пирамида описана около шара E1Q = OQ = TQ = R – радиус шара. EO = PO = r – радиус круга, вписанного в основание пирамиды. SO = H – высота пирамиды.
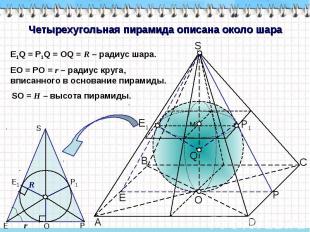
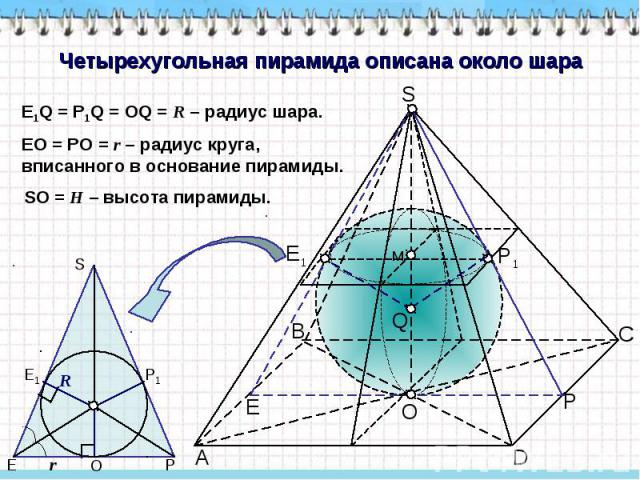
Четырехугольная пирамида описана около шара E1Q = P1Q = OQ = R – радиус шара. EO = PO = r – радиус круга, вписанного в основание пирамиды. SO = H – высота пирамиды.

Задачи Шар вписан в пирамиду. Пирамида вписана в шар. Сфера вписана в конус. Куб вписан в конус. Шар вписан в конус.

В правильную четырехугольную пирамиду вписан шар, объем которого 32/3. Найдите объем пирамиды, если её высота равна 6. Решение. SP1Q – прямоугольный, SP1QSOP (Р1=О=90, S – общий), откуда 5) Тогда сторона основания пирамиды вдвое больше, и равна
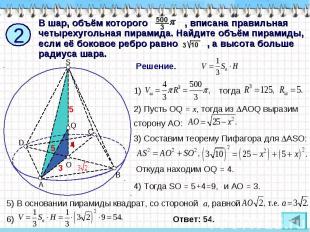
В шар, объём которого , вписана правильная четырехугольная пирамида. Найдите объём пирамиды, если её боковое ребро равно , а высота больше радиуса шара. Решение. 2) Пусть OQ = x, тогда из AOQ выразим сторону АО: 3) Составим теорему Пифагора для ASO: Откуда находим OQ = 4. 4) Тогда SO = 5+4=9, 5) В основании пирамиды квадрат, со стороной a, равной

Площадь поверхности сферы, вписанной в конус, равна 100. Длина окружности, по которой сфера касается поверхности конуса, равна 6. Найдите радиус основания конуса. C = 2r = 6, тогда r = O2P = 3. 2) Sсферы = 4R2 =100, тогда R = O1P = 5. 3) Из O1O2P по теореме Пифагора находим: 4) В O1PS отрезок РО2 высота, проведенная из вершины прямого угла, значит 5) Найдем высоту конуса SO= SO2 +O2O1+O1O = 2,25 + 4 + 5 = 11,25. 6) SО2РSOВ (О2=О=90, S – общий),

В конус с образующей 66 и высотой 12 вписан куб. Найдите объём куба. 1) Из прямоугольного SOP находим: 2) a – сторона куба, тогда 3) Выразим через a: 4) SО1Р1SOР (О1=О=90, S – общий), откуда a = 6. 5) V куба = a3 = 63 = 216.
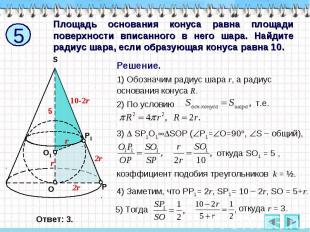
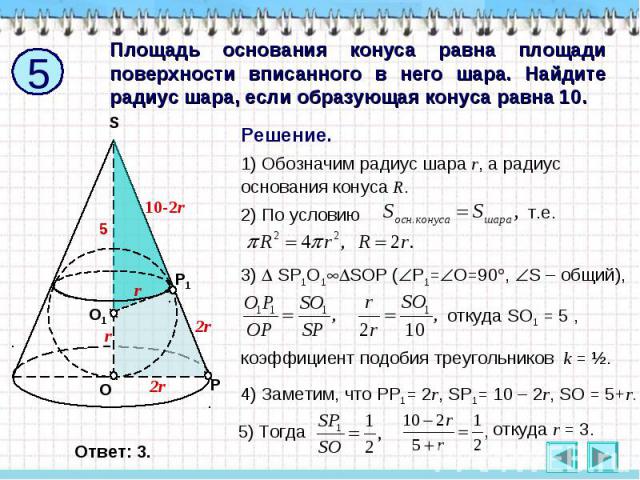
Площадь основания конуса равна площади поверхности вписанного в него шара. Найдите радиус шара, если образующая конуса равна 10. Решение. 1) Обозначим радиус шара r, а радиус основания конуса R. 2) По условию 3) SP1O1SOP (Р1=О=90, S – общий), откуда SO1 = 5 , коэффициент подобия треугольников k = ½. 4) Заметим, что РР1= 2r, SP1= 10 – 2r, SO = 5+r.

Реши самостоятельно Высота конуса равна 6, а объём равен 144. Найдите площадь полной поверхности куба, вписанного в конус. Ответ: Шар объём которого равен 32/3, вписан в конус. Найдите высоту конуса, если радиус его основания равен 23. Ответ: Желаю удачи!

Домашнее задание Реши задачу и оформи решение либо на альбомном листе, либо в виде электронного документа (PowerPoint, Paint, Word и т.д.) Рефлексия Что нового вы узнали на уроке? Чему вы научились? Какое у вас настроение в конце урока? Можете ли вы объяснить решение данных задач однокласснику, пропустившему урок сегодня?

1. Готман Э.Г. Стереометрические задачи и методы их решения. М.: МЦНМО, 2006.— 160 с. 2. Гусев В. А., Литвиненко В. Н., Мордкович А. Г. Практикум по элементарной математике. Геометрия. М.: Просвещение, 1992.3. Комплект таблиц по стереометрии: http://www.varson.ru/geometr_9.html 4. Единый государственный экзамен 2001: Тестовые задания: Математика/С.В. Климин, Т.В. Стрункина, Е.И. Пантелеева и др.; М-во образования РФ. – М.: Просвещение, 20015. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.ru 6. Рисунки на слайдах №6, №12, №13 взяты с сайта: http://office.microsoft.com/ru-ru/images/results.aspx?qu=%D1%81%D0%BC%D0%B0%D0%B9%D0%BB%D1%8B