Презентация на тему: Прямоугольные треугольники

Прямоугольные треугольники

Цели и задачи.1. Усвоение материала через практикум и теорию; 2. Формирование логического мышления; 3. Научиться видеть различие и сходство в доказательствах признаков;4. Пытаться развивать способности обучающихся к самообразованию;5. Формирование умений саморегулирования своей учебно- познавательной деятельности.

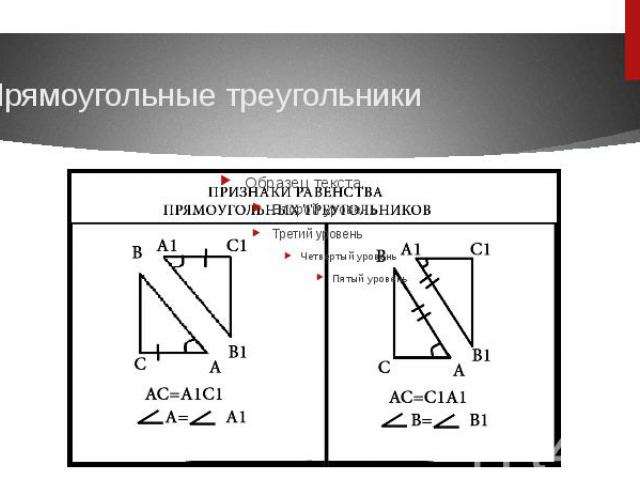
Прямоугольные треугольники Треугольник называется прямоугольным, если у него есть прямой угол. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны – катетами. AC и AB – катеты, BC – гипотенуза.Теорема. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.  

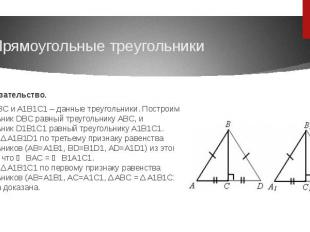
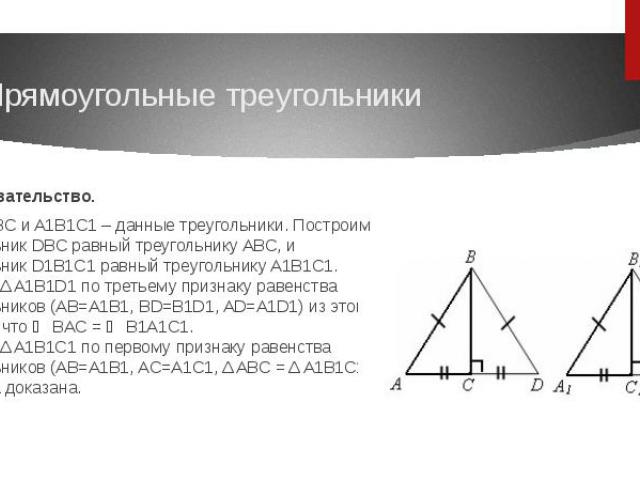
Доказательство. Пусть ABC и A1B1C1 – данные треугольники. Построим треугольник DBC равный треугольнику ABC, и треугольник D1B1C1 равный треугольнику A1B1C1. Δ ABD = Δ A1B1D1 по третьему признаку равенства треугольников (AB=A1B1, BD=B1D1, AD=A1D1) из этого следует, что ∠ BAC = ∠ B1A1C1. Δ ABC = Δ A1B1C1 по первому признаку равенства треугольников (AB=A1B1, AC=A1C1, Δ ABC = Δ A1B1C1). Теорема доказана.

2 признак равенства если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны. 

ДАНО: ΔABC, Δ A1B1C1 Угл C = Углу C1 = 90 °AB = A1B1 Доказать: ΔABC= Δ A1B1C1

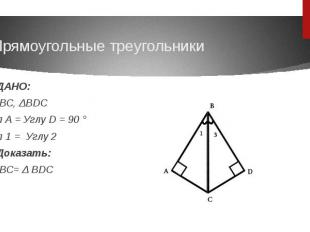
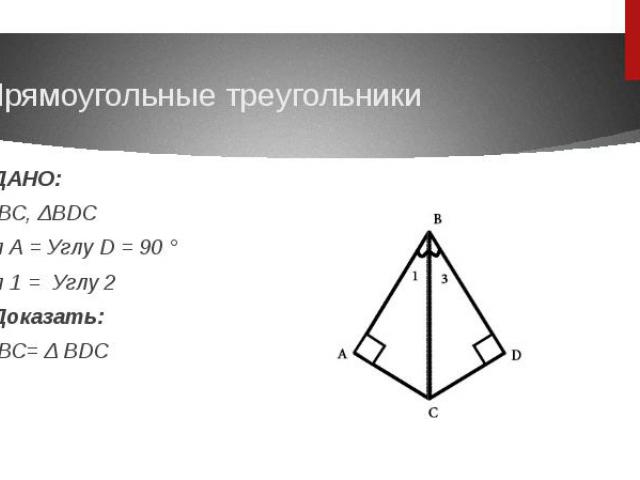
Прямоугольные треугольникиДАНО:ΔABC, ΔBDCУгл A = Углу D = 90 °Угл 1 = Углу 2Доказать: ΔABC= Δ BDC

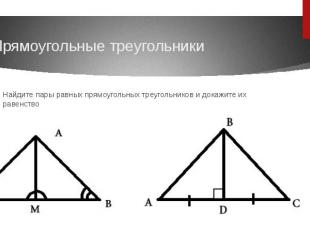
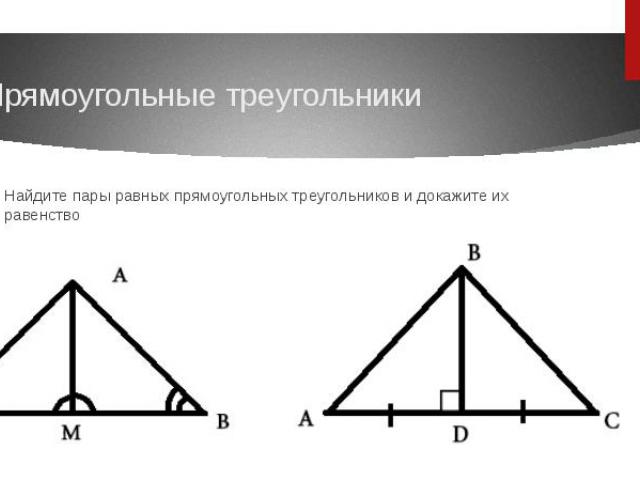
Прямоугольные треугольникиНайдите пары равных прямоугольных треугольников и докажите их равенство

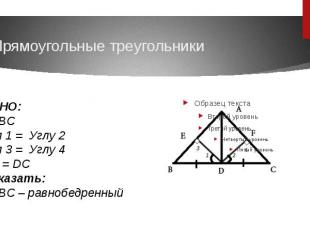
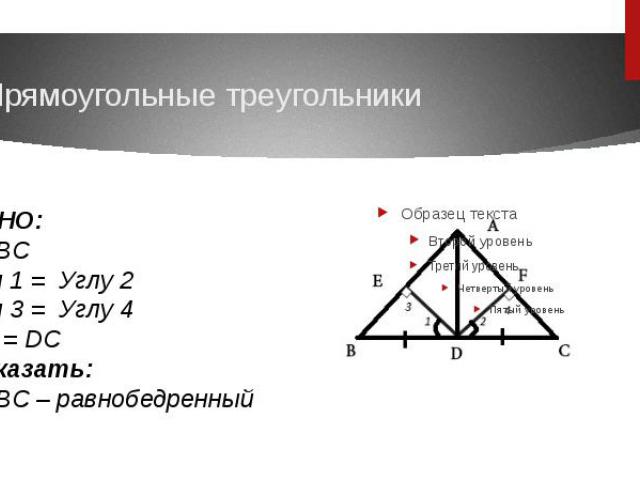
Прямоугольные треугольники

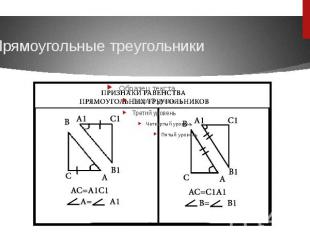
Прямоугольные треугольники

Прямоугольные треугольники Д/З: п: 34,35, №268,№269.