Презентация на тему: Построение сечений пирамиды (тетраэдра)

Построение сеченийпирамиды (тетраэдраУрок-презентацияучителя математики МАОУ СОШ п. ДемянскНовгородской областиВерзиловой Нелли Ильиничны

«Воображение важнее знания. Знание ограничено, воображением можно охватить всё» А. Эйнштейн

1. Целеполагание2. Теоретическая основа3. Устная работа4. Тест. Работа в паре.5. Практикум. Коллективная работа.6. Самостоятельная работа с самопроверкой7. Инструктаж домашнего задания8. Работа в группах: «Составь задачу»9. Рефлексия. Самооценка своей работы.

1.Цель урока Цель- конечный желаемый результатНапиши свою цель урока

1. Цель урокаНаучиться строить сечения тетраэдра

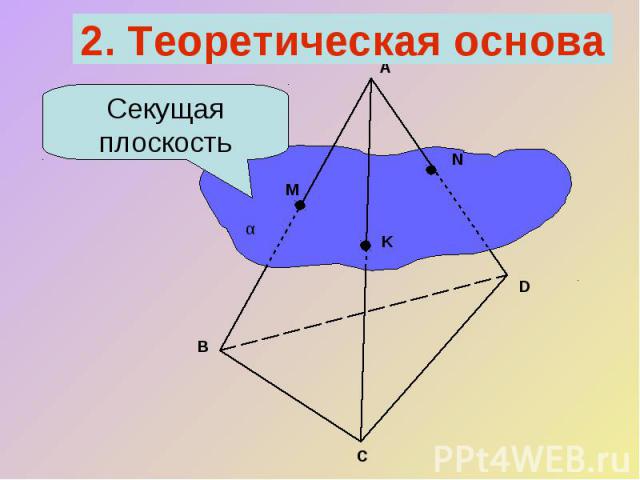
Секущей плоскостью многогранника назовем любую плоскость, по обе стороны от которой имеются точки данного многогранника.Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.2.Теоретическая основа Определение сечения.
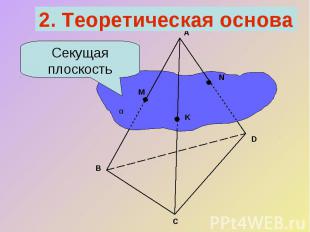
2. Теоретическая основаСекущая плоскость
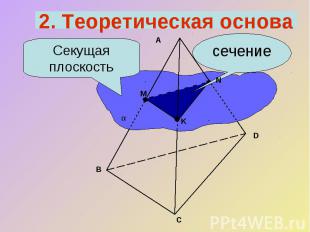
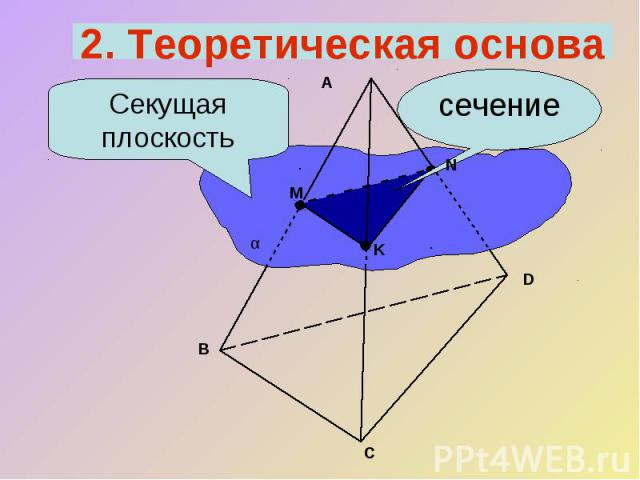
Секущая плоскостьсечение

2.Теоретическая основа Геометрические утвержденияЕсли две точки одной прямой лежат в плоскости, то ився прямая лежит в этой плоскости.

2. Теоретическая основа Геометрические утвержденияЕсли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
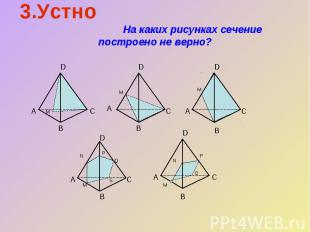
3.Устно На каких рисунках сечение построено не верно?

3. УстноОбъясните, какая теория использованапри построении следующих сечений
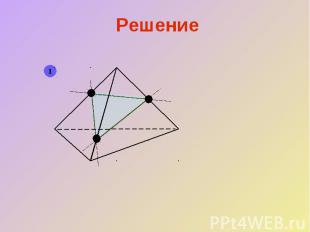
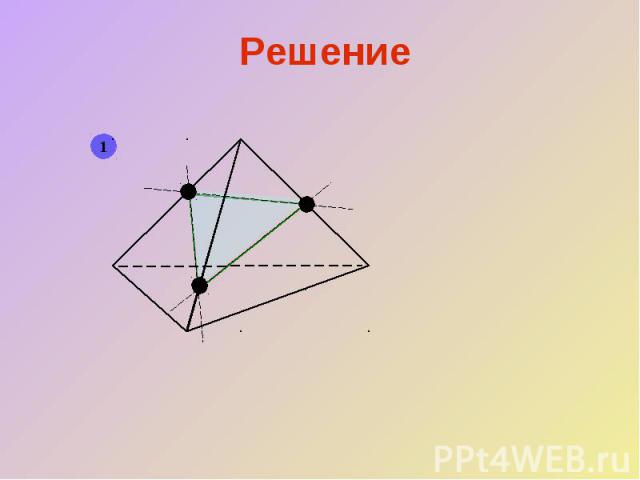
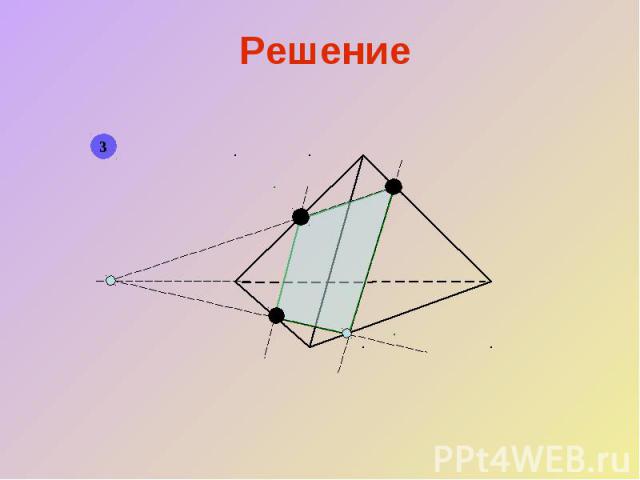
Решение
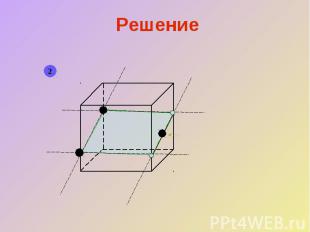
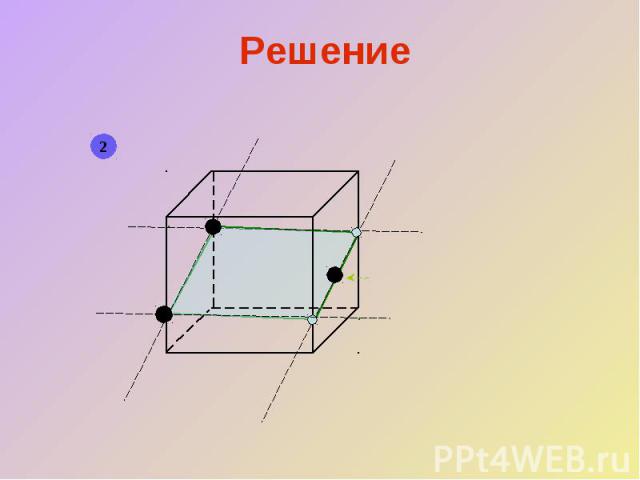
Решение
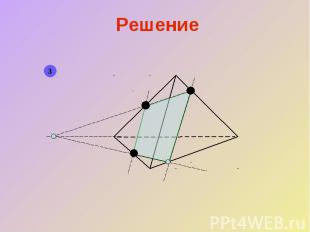
Решение
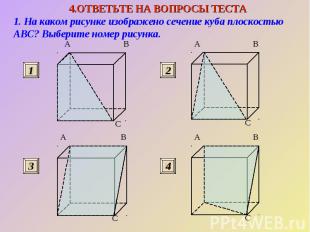
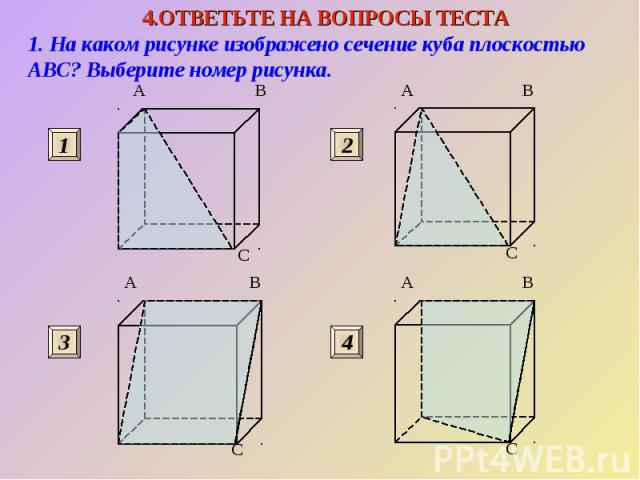
1. На каком рисунке изображено сечение куба плоскостью ABC? Выберите номер рисунка.
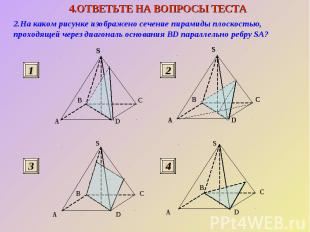
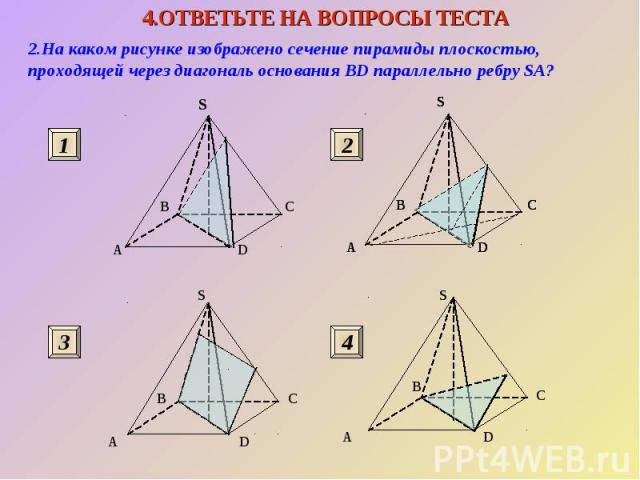
2.На каком рисунке изображено сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру SA?
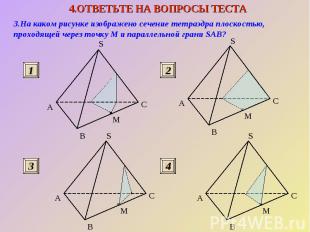
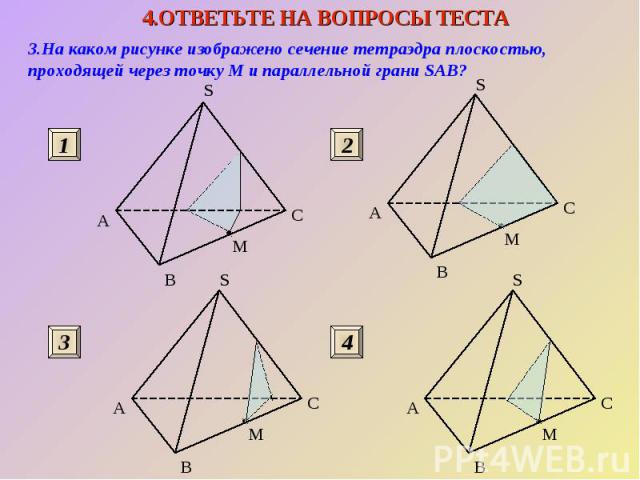
3.На каком рисунке изображено сечение тетраэдра плоскостью, проходящей через точку М и параллельной грани SAВ?

Код теста324
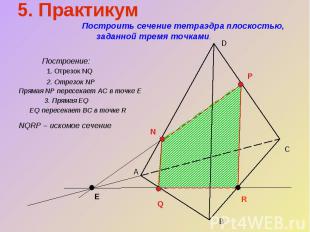
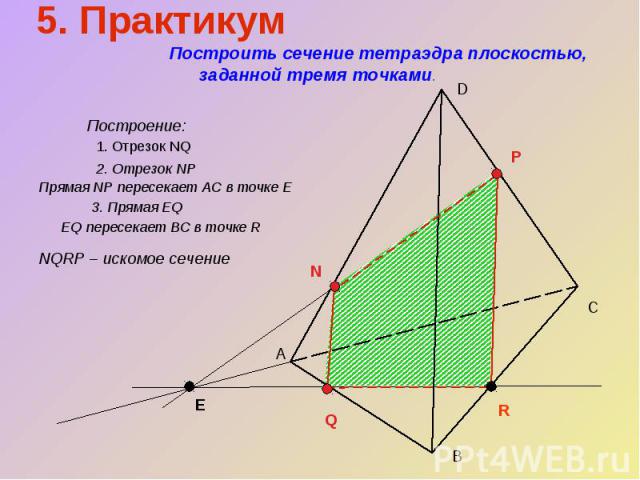
5. Практикум Построить сечение тетраэдра плоскостью, заданной тремя точками.Построение:1. Отрезок NQ2. Отрезок NP Прямая NP пересекает АС в точке Е3. Прямая EQ EQ пересекает BC в точке RNQRP – искомое сечение
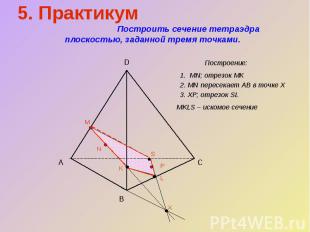
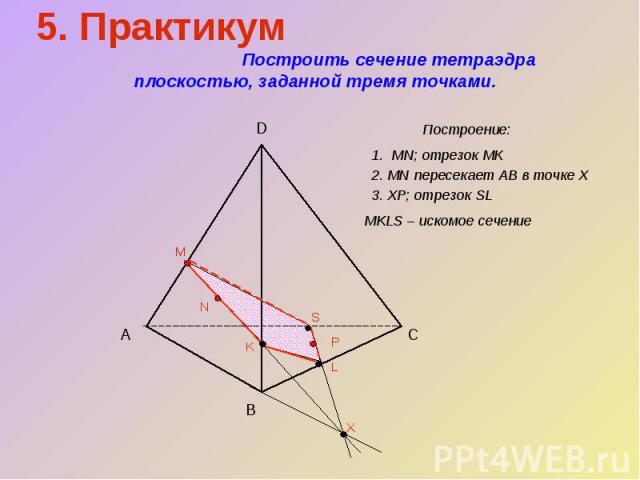
5. Практикум Построить сечение тетраэдра плоскостью, заданной тремя точками.Построение:1. MN; отрезок МК2. MN пересекает АВ в точке Х3. ХР; отрезок SLMKLS – искомое сечение
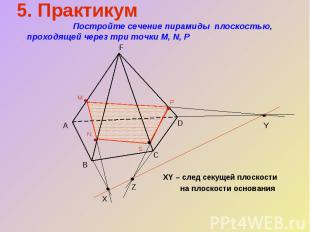
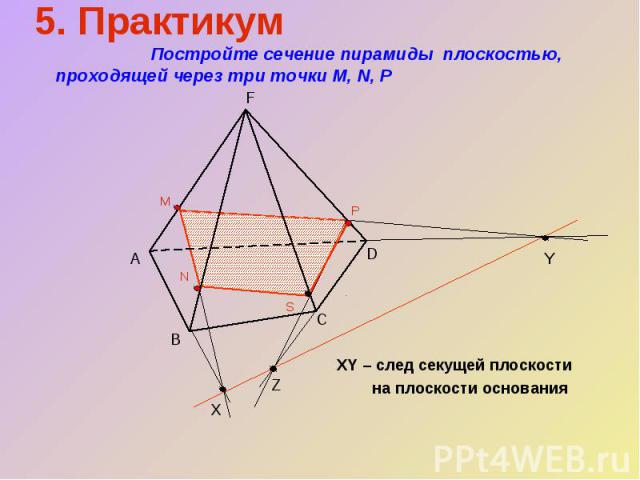
XY – след секущей плоскости на плоскости основания 5. Практикум Постройте сечение пирамиды плоскостью, проходящей через три точки М, N, Р
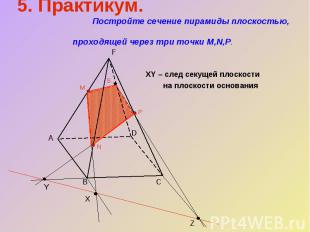
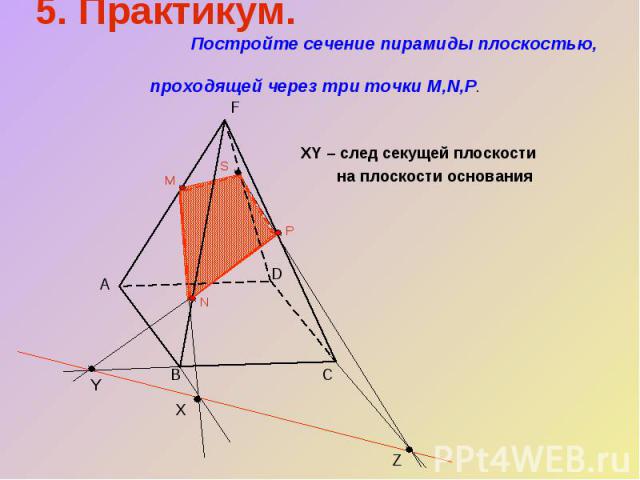
5. Практикум. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P.XY – след секущей плоскости на плоскости основания
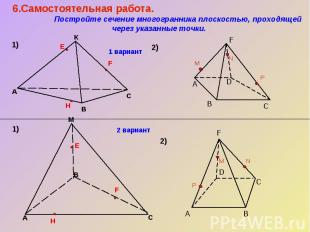
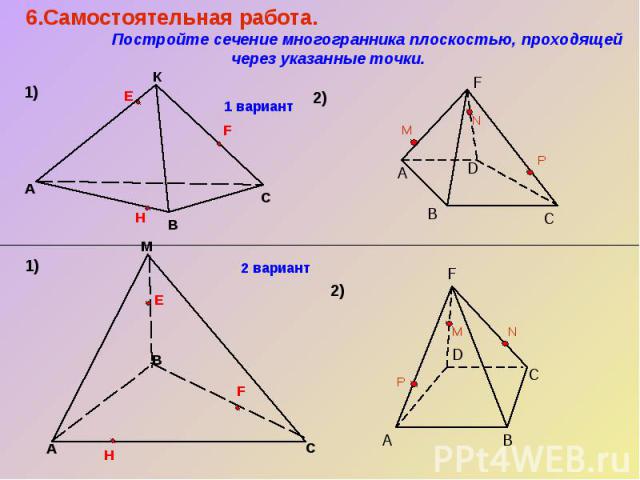
6.Самостоятельная работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки.
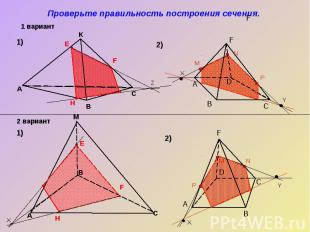
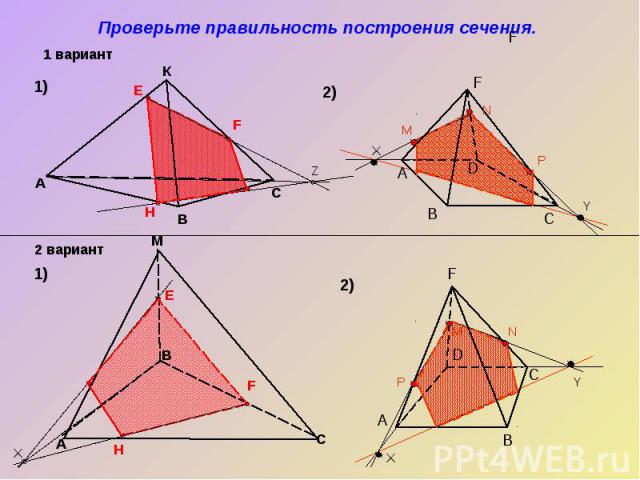
Проверьте правильность построения сечения.

Составить 3-4 задачи на построение сечений многогранников.Выполнить решения в форме презентации или в WORDE. Срок до 10 дней.Критерии оценки: СложностьПравильность решенияДизайн

8. Работа в группахЗадайте плоскость сечения куба 3-мя точками так, чтобы она не пересекала только 1группа: верхнюю грань2группа: правую грань 3 группа: левую грань4 группа: нижнюю грань Постройте заданное вами сечение

Критерии самооценки:Тест 0,1,2,3 балла «5» - 15 баллов +Устная работа 1-2 балла «4» - 10-14 балловПрактикум 1-3баллаСам. работа 3; 5 балловСост. задачи 3-5 баллов В чём я вижу результат своей работы? Что мне помогло достичь результата?9. Подведение итогов работы на уроке

Китайская пословица Не бойся, что не знаешь - бойся, что не учишься.

Использованные материалы1) Сайт www. uchportal.ru О.П. Беляева «Построение сечений многогранника»2) Газета «Математика» №6, 2010 И. Тельманова, стр. 11-14 «Построение сечений многогранника»