Презентация на тему: Объём призмы

Курсовая работа учителя математики школы №13 с углубленным изучением английского языка Виноградовой Ольги Васильевны.

ОБЪЁМ ПРИЗМЫ. ПЛАН ТЕМЫ:I. Понятие объема. II. Основные свойства объёмов. III. Объём произвольной призмы.

Понятие объема Объем каждого тела выражается положительным числом, которое показывает, сколько единиц измерения объемов и частей единицы содержится в данном теле.

За единицу объема принят объем куба, ребро которого равно единице длины.

Чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения.

Общие свойства объемов тел: I. Равные тела имеют равные объемы, при перемещении тела его объем не изменяется. II. Если тело разбить на части, являющиеся простыми телами, то объем тела равен сумме объемов этих частей.

Рассмотрим первое свойство. Равные тела имеют равные объемы, при перемещении тела его объем не изменяется;

Рассмотрим второе свойство. Если тело разбить на части, являющиеся простыми телами, то объем тела равен сумме объемов всех частей.

Формула объёма прямоугольного параллелепипеда.

Объем прямой треугольной призмы, в основании которой лежит прямоугольный треугольник, равен произведению площади основания на высоту.
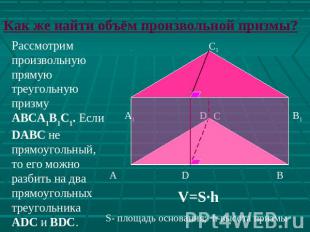
Как же найти объём произвольной призмы? Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если DABC не прямоугольный, то его можно разбить на два прямоугольных треугольника ADC и BDC.

Пусть дана n – угольная прямая призма (n>3). Разобьем ее на конечное число прямых треугольных призм.По свойству объемов, сложив объемы этих треугольных призм, получим объем данной.

Наклонная призма равновелика такой прямой призме, у которой основанием служит перпендикулярное сечение наклонной призмы, а высотой – боковое ребро данной наклонной призмы.