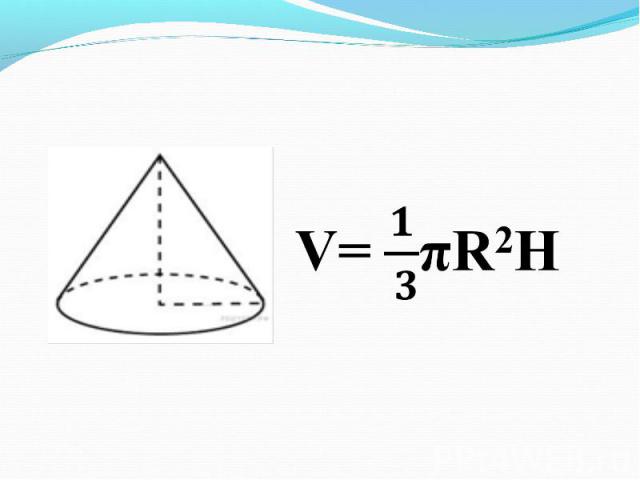
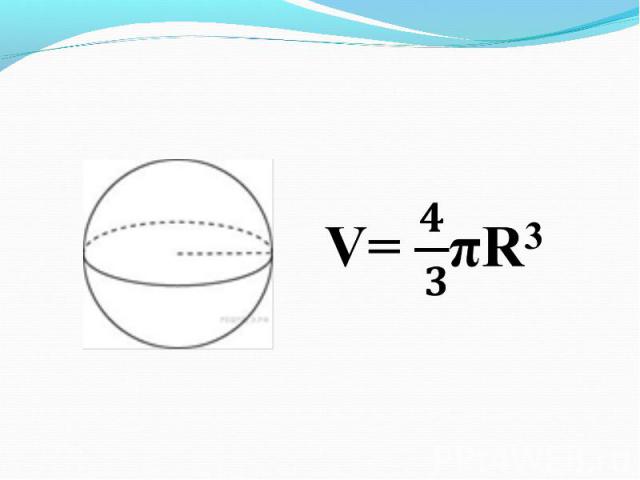
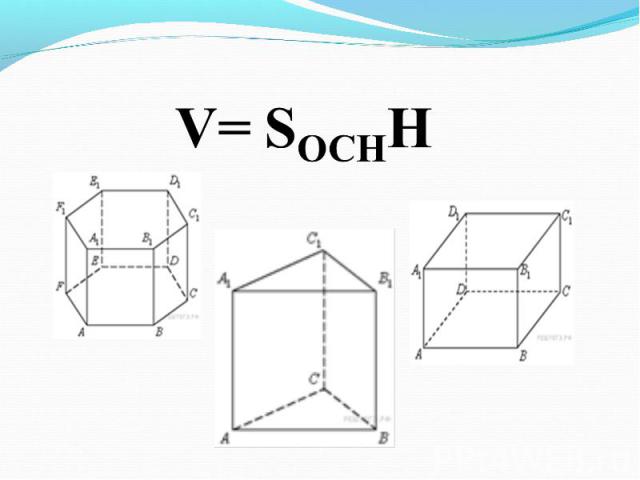
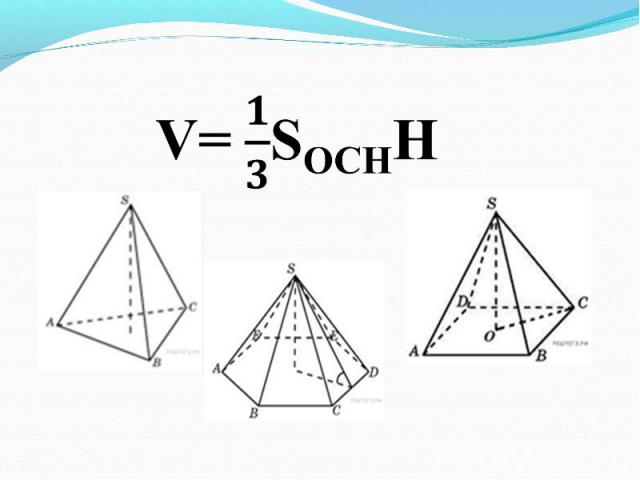
Презентация на тему: Объемы тел"

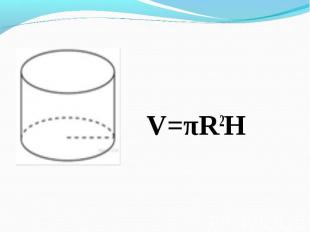
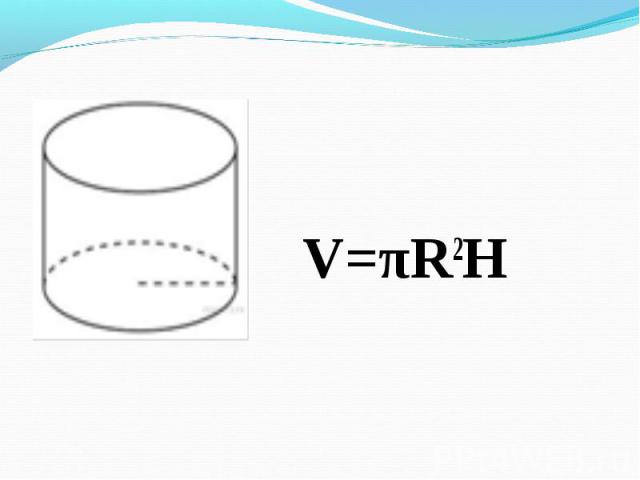
V=πR2H
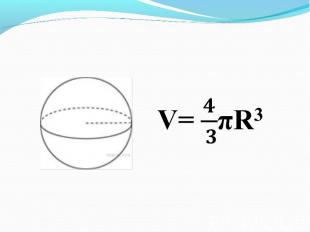
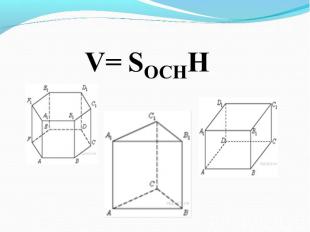
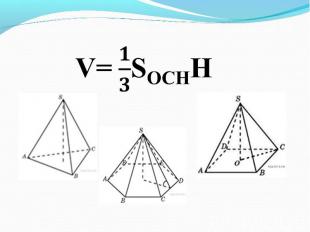

Цилиндр и конус имеют общее основание и общую высоту. Вычислите объём цилиндра, если объём конуса равен 25. Цилиндр и конус имеют общее основание и общую высоту. Вычислите объём цилиндра, если объём конуса равен 25. Ответ: 75

Цилиндр и конус имеют общие основание и высоту. Найдите объём конуса, если объём цилиндра равен 150. Цилиндр и конус имеют общие основание и высоту. Найдите объём конуса, если объём цилиндра равен 150. Ответ:50

Объем ко­ну­са равен 16. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са. Объем ко­ну­са равен 16. Через се­ре­ди­ну вы­со­ты па­рал­лель­но ос­но­ва­нию ко­ну­са про­ве­де­но се­че­ние, ко­то­рое яв­ля­ет­ся ос­но­ва­ни­ем мень­ше­го ко­ну­са с той же вер­ши­ной. Най­ди­те объем мень­ше­го ко­ну­са. Ре­ше­ние. Боль­ший конус по­до­бен мень­ше­му с ко­эф­фи­ци­ен­том 2. Объ­е­мы по­доб­ных тел от­но­сят­ся как куб ко­эф­фи­ци­ен­та по­до­бия. По­это­му объем мень­ше­го ко­ну­са в во­семь раз мень­ше объ­е­ма боль­ше­го ко­ну­са. Ответ: 8

Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 3 раза? Во сколь­ко раз умень­шит­ся объем ко­ну­са, если его вы­со­ту умень­шить в 3 раза? Ре­ше­ние. Объем ко­ну­са равен где S – пло­щадь ос­но­ва­ния, а h – вы­со­та ко­ну­са. При умень­ше­нии вы­со­ты в 3 раза объем ко­ну­са также умень­шит­ся в 3 раза. Ответ: 3.

Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 1,5 раза? Во сколь­ко раз уве­ли­чит­ся объем ко­ну­са, если его ра­ди­ус ос­но­ва­ния уве­ли­чить в 1,5 раза? Ре­ше­ние. Объем ко­ну­са равен где – пло­щадь ос­но­ва­ния, – вы­со­та ко­ну­са, а – ра­ди­ус ос­но­ва­ния. При уве­ли­че­нии ра­ди­у­са ос­но­ва­ния в 1,5 раза объем ко­ну­са уве­ли­чит­ся в 2,25 раза. Ответ: 2,25.

В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет вы­со­ты. Объём жид­ко­сти равен 70 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд? В со­су­де, име­ю­щем форму ко­ну­са, уро­вень жид­ко­сти до­сти­га­ет вы­со­ты. Объём жид­ко­сти равен 70 мл. Сколь­ко мил­ли­лит­ров жид­ко­сти нужно до­лить, чтобы пол­но­стью на­пол­нить сосуд? Ре­ше­ние. Мень­ший конус по­до­бен боль­ше­му с ко­эф­фи­ци­ен­том 0,5. Объ­е­мы по­доб­ных тел от­но­сят­ся как куб ко­эф­фи­ци­ен­та по­до­бия. По­это­му объем боль­ше­го ко­ну­са в 8 раз боль­ше объ­е­ма мень­ше­го ко­ну­са, он равен 560 мл. Сле­до­ва­тель­но, не­об­хо­ди­мо до­лить 560 − 70 = 490 мл жид­ко­сти. Ответ: 490.

Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния и вы­со­та ко­то­ро­го равны 1. Най­ди­те объем па­рал­ле­ле­пи­пе­да. Пря­мо­уголь­ный па­рал­ле­ле­пи­пед опи­сан около ци­лин­дра, ра­ди­ус ос­но­ва­ния и вы­со­та ко­то­ро­го равны 1. Най­ди­те объем па­рал­ле­ле­пи­пе­да. Ре­ше­ние. Вы­со­та па­рал­ле­ле­пи­пе­да равна вы­со­те впи­сан­но­го в него ци­лин­дра. Ос­но­ва­ни­ем па­рал­ле­ле­пи­пе­да яв­ля­ет­ся квад­рат, сто­ро­на ко­то­ро­го в два раза боль­ше ра­ди­у­са впи­сан­ной в него окруж­но­сти. По­это­му пло­щадь ос­но­ва­ния равна 4, а объем па­рал­ле­ле­пи­пе­да равен Ответ: 4.

В куб впи­сан шар ра­ди­у­са 1. Най­ди­те объем куба. В куб впи­сан шар ра­ди­у­са 1. Най­ди­те объем куба. Ре­ше­ние. Ребро куба равно диа­мет­ру впи­сан­но­го в него шара, а объем куба равен кубу его ребра. От­сю­да имеем: Ответ: 8.

Во сколь­ко раз объем ко­ну­са, опи­сан­но­го около пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды, боль­ше объ­е­ма ко­ну­са, впи­сан­но­го в эту пи­ра­ми­ду? Во сколь­ко раз объем ко­ну­са, опи­сан­но­го около пра­виль­ной че­ты­рех­уголь­ной пи­ра­ми­ды, боль­ше объ­е­ма ко­ну­са, впи­сан­но­го в эту пи­ра­ми­ду? Ре­ше­ние. Объ­е­мы дан­ных ко­ну­сов со­от­но­сят­ся как пло­ща­ди их ос­но­ва­ний, и, сле­до­ва­тель­но, как квад­ра­ты их диа­мет­ров. Диа­метр впи­сан­но­го ко­ну­са равен сто­ро­не квад­ра­та, диа­метр опи­сан­но­го – диа­го­на­ли квад­ра­та, длина ко­то­рой равна длины сто­ро­ны. По­это­му объем опи­сан­но­го ко­ну­са в 2 раза боль­ше объ­е­ма впи­сан­но­го. Ответ: 2.

Объём тет­ра­эд­ра равен 19. Най­ди­те объём мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся се­ре­ди­ны рёбер дан­но­го тетра­эд­ра. Объём тет­ра­эд­ра равен 19. Най­ди­те объём мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся се­ре­ди­ны рёбер дан­но­го тетра­эд­ра. Ре­ше­ние. Объем дан­но­го мно­го­гран­ни­ка равен раз­но­сти объ­е­мов ис­ход­но­го тет­ра­эд­ра и че­ты­рех тет­ра­эд­ров, одни из вер­шин ко­то­рых сов­па­да­ют с вер­ши­на­ми ис­ход­но­го: Ответ: 9,5.

Ци­линдр опи­сан около шара. Объем ци­лин­дра равен 33. Най­ди­те объем шара. Ци­линдр опи­сан около шара. Объем ци­лин­дра равен 33. Най­ди­те объем шара. Ре­ше­ние. Вы­ра­зим из фор­му­лы для объёма ци­лин­дра и под­ста­вим в фор­му­лу для объёма шара Ответ: 22.

Ци­линдр опи­сан около шара. Объем шара равен 24. Най­ди­те объем ци­лин­дра. Ци­линдр опи­сан около шара. Объем шара равен 24. Най­ди­те объем ци­лин­дра. Ре­ше­ние. Объем ци­лин­дра равен про­из­ве­де­нию пло­ща­ди ос­но­ва­ния на вы­со­ту. Пло­щадь ос­но­ва­ния ци­лин­дра равна пло­ща­ди боль­шо­го круга впи­сан­но­го шара, а вы­со­та ци­лин­дра равна диа­мет­ру впи­сан­но­го шара. По­это­му Ответ: 36.

Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B, C, D1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1, у ко­то­ро­го AB=4, AD=3 , AA1=4. Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B, C, D1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1, у ко­то­ро­го AB=4, AD=3 , AA1=4. Решение. Пло­щадь ос­но­ва­ния пи­ра­ми­ды в два раза мень­ше пло­ща­ди ос­но­ва­ния па­рал­ле­ле­пи­пе­да, а вы­со­та у них общая. По­это­му Ответ: 8.

Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A1,B,C, C1, B1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1, у ко­то­ро­го AB=4, AD=3, AA1=4. Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A1,B,C, C1, B1 пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA1B1C1D1, у ко­то­ро­го AB=4, AD=3, AA1=4. Решение. Ос­но­ва­ни­ем пи­ра­ми­ды, объем ко­то­рой нужно найти, яв­ля­ет­ся бо­ко­вая грань па­рал­ле­ле­пи­пе­да, а ее вы­со­той яв­ля­ет­ся ребро A1B1. По­это­му Ответ: 16.

В сосуд, име­ю­щий форму пра­виль­ной тре­уголь­ной приз­мы, на­ли­ли 2300 см3воды и по­гру­зи­ли в воду де­таль. При этом уро­вень воды под­нял­ся с от­мет­ки 25 см до от­мет­ки 27 см. Най­ди­те объем де­та­ли. В сосуд, име­ю­щий форму пра­виль­ной тре­уголь­ной приз­мы, на­ли­ли 2300 см3воды и по­гру­зи­ли в воду де­таль. При этом уро­вень воды под­нял­ся с от­мет­ки 25 см до от­мет­ки 27 см. Най­ди­те объем де­та­ли. Ре­ше­ние. Объём де­та­ли равен объ­ёму вы­тес­нен­ной ею жид­ко­сти. Объём вы­тес­нен­ной жид­ко­сти равен 2/25 ис­ход­но­го объёма: Ответ: 184.

В сосуд, име­ю­щий форму пра­виль­ной тре­уголь­ной приз­мы, на­ли­ли воду. Уро­вень воды до­сти­га­ет 80 см. На какой вы­со­те будет на­хо­дить­ся уро­вень воды, если ее пе­ре­лить в дру­гой такой же сосуд, у ко­то­ро­го сто­ро­на ос­но­ва­ния в 4 раза боль­ше, чем у пер­во­го? Ответ вы­ра­зи­те в см. В сосуд, име­ю­щий форму пра­виль­ной тре­уголь­ной приз­мы, на­ли­ли воду. Уро­вень воды до­сти­га­ет 80 см. На какой вы­со­те будет на­хо­дить­ся уро­вень воды, если ее пе­ре­лить в дру­гой такой же сосуд, у ко­то­ро­го сто­ро­на ос­но­ва­ния в 4 раза боль­ше, чем у пер­во­го? Ответ вы­ра­зи­те в см. Ре­ше­ние. Объем приз­мы равен про­из­ве­де­нию пло­ща­ди ее ос­но­ва­ния на вы­со­ту и вы­ра­жа­ет­ся через сто­ро­ну ос­но­ва­ния а и вы­со­ту Н фор­му­лой По­это­му , а зна­чит, при уве­ли­че­нии сто­ро­ны а в 4 раза зна­ме­на­тель уве­ли­чит­ся в 16 раз, то есть вы­со­та умень­шит­ся в 16 раз и будет равна 5 см. Ответ: 5.

Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B,C, D,E, F,A1 пра­виль­ной ше­сти­уголь­ной приз­мы ABCDEFA1B1C1D1E1F1, пло­щадь ос­но­ва­ния ко­то­рой равна 4, а бо­ко­вое ребро равно 3. Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B,C, D,E, F,A1 пра­виль­ной ше­сти­уголь­ной приз­мы ABCDEFA1B1C1D1E1F1, пло­щадь ос­но­ва­ния ко­то­рой равна 4, а бо­ко­вое ребро равно 3. Ре­ше­ние. Ос­но­ва­ние пи­ра­ми­ды такое же, как ос­но­ва­ние пра­виль­ной ше­сти­уголь­ной приз­мы, и вы­со­та у них общая. По­это­му Ответ: 4.

Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B, C, B1 пра­виль­ной ше­сти­уголь­ной приз­мы ABCDEFA1B1C1D1E1F1, пло­щадь ос­но­ва­ния ко­то­рой равна 6, а бо­ко­вое ребро равно 3. Най­ди­те объем мно­го­гран­ни­ка, вер­ши­на­ми ко­то­ро­го яв­ля­ют­ся точки A, B, C, B1 пра­виль­ной ше­сти­уголь­ной приз­мы ABCDEFA1B1C1D1E1F1, пло­щадь ос­но­ва­ния ко­то­рой равна 6, а бо­ко­вое ребро равно 3. Ре­ше­ние. Пло­щадь ос­но­ва­ния тре­уголь­ной пи­ра­ми­ды равна одной ше­стой пло­ща­ди ос­но­ва­ния пра­виль­ной ше­сти­уголь­ной приз­мы, а вы­со­та у них общая. По­это­му Ответ: 1.

Во сколь­ко раз уве­ли­чит­ся объем пра­виль­но­го тет­ра­эд­ра, если все его ребра уве­ли­чить в два раза? Во сколь­ко раз уве­ли­чит­ся объем пра­виль­но­го тет­ра­эд­ра, если все его ребра уве­ли­чить в два раза? Ре­ше­ние. Объёмы по­доб­ных тел от­но­сят­ся как куб ко­эф­фи­ци­ен­та по­до­бия. По­это­му если все ребра уве­ли­чить в 2 раза, объём уве­ли­чит­ся в 8 раз. Это же сле­ду­ет из фор­му­лы для объёма пра­виль­но­го тет­ра­эд­ра , где a — длина его ребра. Ответ: 8.

Во сколь­ко раз уве­ли­чит­ся объем пи­ра­ми­ды, если ее вы­со­ту уве­ли­чить в че­ты­ре раза? Во сколь­ко раз уве­ли­чит­ся объем пи­ра­ми­ды, если ее вы­со­ту уве­ли­чить в че­ты­ре раза? Ре­ше­ние. Объем пи­ра­ми­ды равен где S – пло­щадь ос­но­ва­ния, а h – вы­со­та пи­ра­ми­ды. При уве­ли­че­нии вы­со­ты в 4 раза объем пи­ра­ми­ды также уве­ли­чит­ся в 4 раза. Ответ: 4.

Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/π. Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/π. Ре­ше­ние. Объем дан­ной части ци­лин­дра равен Ответ: 144.

Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/π . Най­ди­те объем V части ци­лин­дра, изоб­ра­жен­ной на ри­сун­ке. В от­ве­те ука­жи­те V/π . Ре­ше­ние. Объем дан­ной части ци­лин­дра равен Ответ: 937,5.

16-1.В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC бо­ко­вое ребро равно 5, а сто­ро­на ос­но­ва­ния равна 6. Най­ди­те рас­сто­я­ние от вер­ши­ны A до плос­ко­сти SBC. 16-1.В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC бо­ко­вое ребро равно 5, а сто­ро­на ос­но­ва­ния равна 6. Най­ди­те рас­сто­я­ние от вер­ши­ны A до плос­ко­сти SBC. Ре­ше­ние. Пусть SO – вы­со­та пи­ра­ми­ды. Тогда Пусть V – объём пи­ра­ми­ды, тогда С дру­гой сто­ро­ны, где h – ис­ко­мое рас­сто­я­ние. В тре­уголь­ни­ке SBC вы­со­та SM равна Пло­щадь тре­уголь­ни­ка SBC равна По­лу­ча­ем, что Ответ:


Список используемой литературы и ресурсов : Список используемой литературы и ресурсов : 1. ЕГЭ-2015.Математика.50 вариантов типовых тестовых заданий / под ред. И.В.Ященко. – М.: Издательство «Экзамен», 2015 3.mathege.ru 4.reshuege.ru