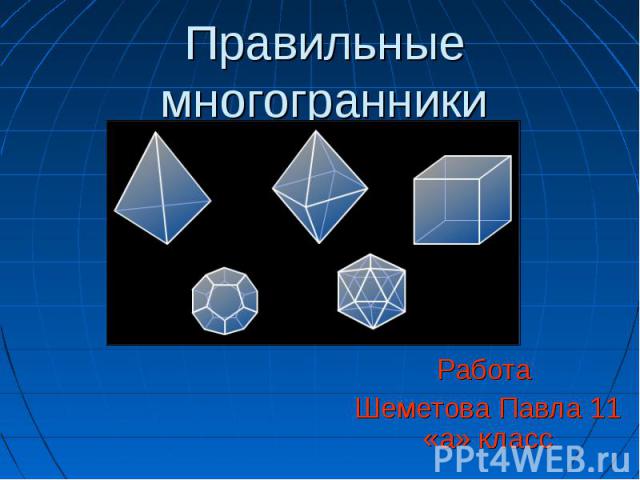
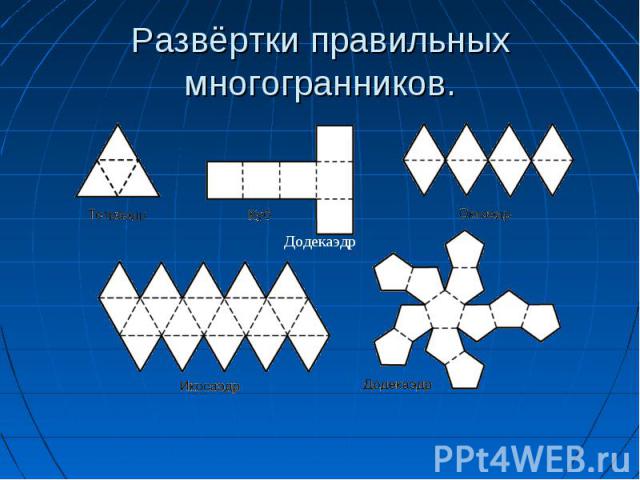
Презентация на тему: Правильные многогранники.

Цель пректа Цель пректа Термин Многогранники История Платон Платоновы тела Евклид Архимед Архимедовы тела Иоганн Кеплер Космологическая гипотеза Кеплера

Рассказать о правильных многогранниках, о их происхождении, их нахождении в природе, архитектуре и живописи. Рассказать о правильных многогранниках, о их происхождении, их нахождении в природе, архитектуре и живописи.

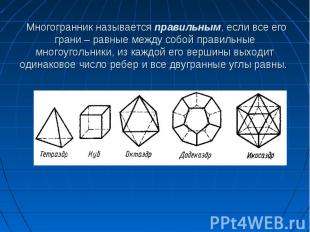
Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами. Их изучали ученые, ювелиры, священники, архитекторы. Этим многогранникам даже приписывали магические свойства. Древнегреческий ученый и философ Платон (IV–V в до н. э.) считал, что эти тела олицетворяют сущность природы. В своем диалоге «Тимей» Платон говорит, что атом огня имеет вид тетраэдра, земли – гексаэдра (куба), воздуха – октаэдра, воды – икосаэдра. В этом соответствии не нашлось места только додекаэдру и Платон предположил существование еще одной, пятой сущности – эфира, атомы которого как раз и имеют форму додекаэдра. Ученики Платона продолжили его дело в изучении перечисленных тел. Поэтому эти многогранники называют платоновыми телами.

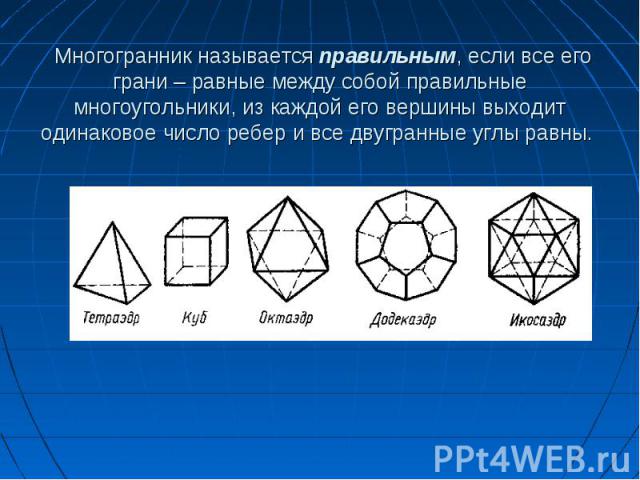
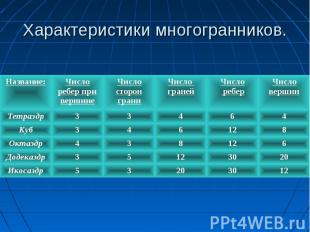
«эдра» - грань «эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «дедека» - 12

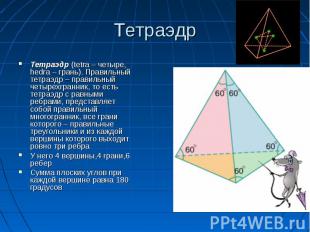
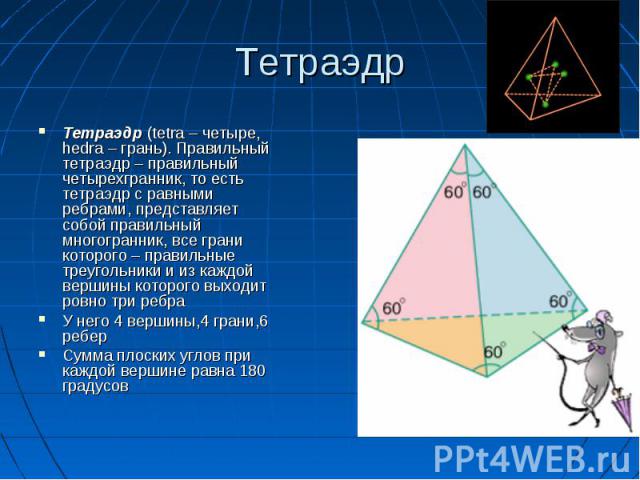
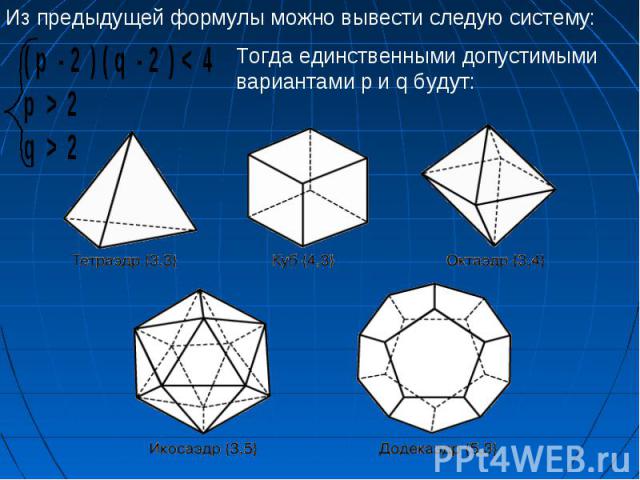
Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра Тетраэдр (tetra – четыре, hedra – грань). Правильный тетраэдр – правильный четырехгранник, то есть тетраэдр с равными ребрами, представляет собой правильный многогранник, все грани которого – правильные треугольники и из каждой вершины которого выходит ровно три ребра У него 4 вершины,4 грани,6 ребер Сумма плоских углов при каждой вершине равна 180 градусов

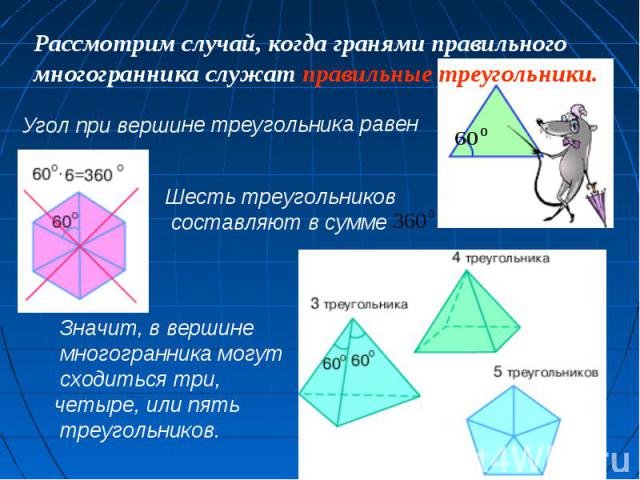
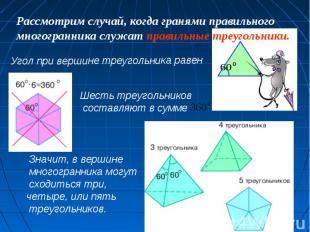
(состоит из 20 треугольников) В каждой вершине икосаэдра сходятся пять граней. Существует правильный многогранник, у которого все грани – правильные треугольники, и из каждой вершины выходит 5 ребер. Этот многогранник имеет 20 граней, 30 ребер, 12 вершин и называется икосаэдром (icosi – двадцать). Сумма плоских углов при каждой вершине равна 300 градусов

Существует правильный многогранник, у которого все грани правильные пятиугольники и из каждой вершины выходит 3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать). Существует правильный многогранник, у которого все грани правильные пятиугольники и из каждой вершины выходит 3 ребра. Этот многогранник имеет 12 граней, 30 ребер и 20 вершин и называется додекаэдром (dodeka – двенадцать). Сумма плоских углов при каждой вершине равна 324 градуса

Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. Гексаэдр (куб, hexa – шесть). Гексаэдр – правильный многогранник, все грани которого – квадраты, и из каждой вершины выходит три ребра. У него 6 граней,8 вершин,12 ребер Сумма плоских углов при каждой вершине равна 270 градусов

Октаэдр. Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани Октаэдр. Это правильный многогранник, все грани которого – правильные треугольники и к каждой вершине прилегают четыре грани У него 8 граней,12 ребер,6вершин

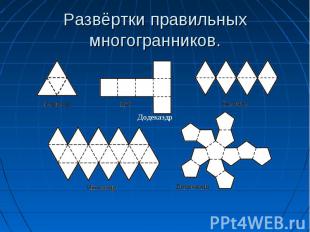
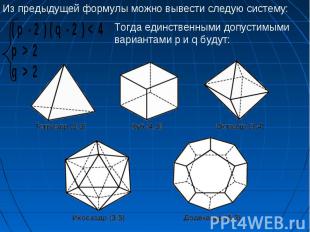
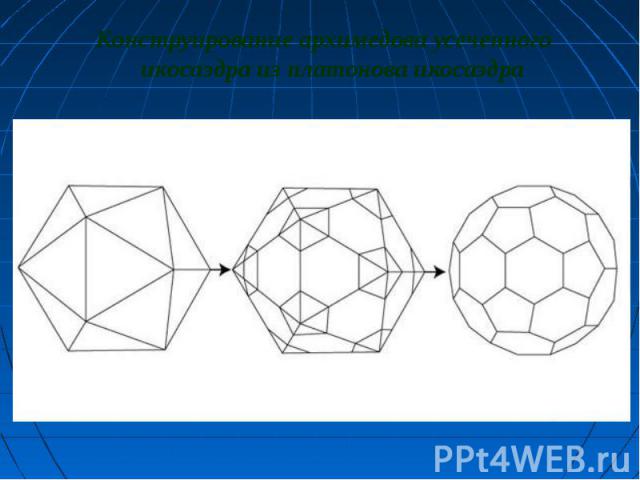
Курносый куб. Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Курносый куб. Этот многогранник можно вписать в куб таким образом, что плоскости шести квадратных его граней совпадут с плоскостями граней куба, причем эти квадратные грани курносого куба окажутся как бы слегка повернутыми по отношению к соответственным граням куба. Ромбоикосододекаэдр. Эта модель принадлежит к числу наиболее привлекательных среди всех других моделей архимедовых тел. Гранями являются треугольники, квадраты и пятиугольники. Ромбоусеченный кубооктаэдр. Этот многогранник, известный также под названием усеченного кубооктаэдра, гранями имеет квадраты, шестиугольники и восьмиугольники. Курносый додекаэдр – это последний из семейства выпуклых однородных многогранников. Гранями являются треугольники и пятиугольники.

Он образован помощью семи кубов, образующих пространственный "крест« и додекаэдра. Он образован помощью семи кубов, образующих пространственный "крест« и додекаэдра.

В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl . Такие кристаллы называются ионными. В кристаллических телах частицы располагаются в строгом порядке, образуя пространственные периодически повторяющиеся структуры во всем объеме тела. Для наглядного представления таких структур используются пространственные кристаллические решетки, в узлах которых располагаются центры атомов или молекул данного вещества. Чаще всего кристаллическая решетка строится из ионов (положительно и отрицательно заряженных) атомов, которые входят в состав молекулы данного вещества. Например, решетка поваренной соли содержит ионы Na+ и Cl–, не объединенные попарно в молекулы NaCl . Такие кристаллы называются ионными.

Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо). Кристаллические решетки металлов часто имеют форму шестигранной призмы (цинк, магний), гранецентрированного куба (медь, золото) или объемно центрированного куба (железо). Кристаллические тела могут быть монокристаллами и поликристаллами. Поликристаллические тела состоят из многих сросшихся между собой хаотически ориентированных маленьких кристалликов, которые называются кристаллитами. Большие монокристаллы редко встречаются в природе и технике. Чаще всего кристаллические твердые тела, в том числе и те, которые получаются искусственно, являются поликристаллами.

Кальций. При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма . Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Кальций. При ударах кристаллы кальцита раскалываются правильные фигурки, каждая грань которых имеет форму параллелограмма . Кальций образует разнообразные кристаллы от пластичной до вытянуто- призматичной формы. Апатит. Они образуют кристаллы в форме прямоугольной призмы. Бериллий. Обычно встречается в виде столбчатых шестигранных кристаллов.

В эпоху Возрождения большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, ХУДОЖНИКИ. Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга, монаха Луки Пачоли «О божественной пропорции» В эпоху Возрождения большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, ХУДОЖНИКИ. Леонардо да Винчи увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга, монаха Луки Пачоли «О божественной пропорции»

На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. На картине художника Сальвадора Дали «Тайная Вечеря» Христос со своими учениками изображён на фоне огромного прозрачного додекаэдра. Форму додекаэдра, по мнению древних, имела  ВСЕЛЕННАЯ , т.е. они считали, что мы живём внутри свода, имеющего форму поверхности  правильного додекаэдра.

Альбрехт Дюрер. Альбрехт Дюрер. В его известной гравюре «Меланхолия» на переднем плане изображен додекаэдр. А в 1525 году Дюрер написал трактат, в котором рассмотрел пять правильных многогранников, поверхности которых служат хорошими моделями перспективы.

Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 6∙6 до 10∙10 м. Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 6∙6 до 10∙10 м.

Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 6∙6 до 10∙10 м. Среди египетских пирамид особое место занимает пирамида фараона Хеопса. Длина стороны её основания L =233,16 м; высота Н =146,6; 148,2 м. Первоначально высота оценивалась не точно. Это связано с осадкой швов, деформацией блоков, предполагаемой частичной разборкой вершины от S 6∙6 до 10∙10 м. Угол наклона граней =51◦51 . Впервые он был измерен английским полковником Г. Вайзовым в 1837 г tg 51◦ 51 =1,27306= vd= 1,27202.

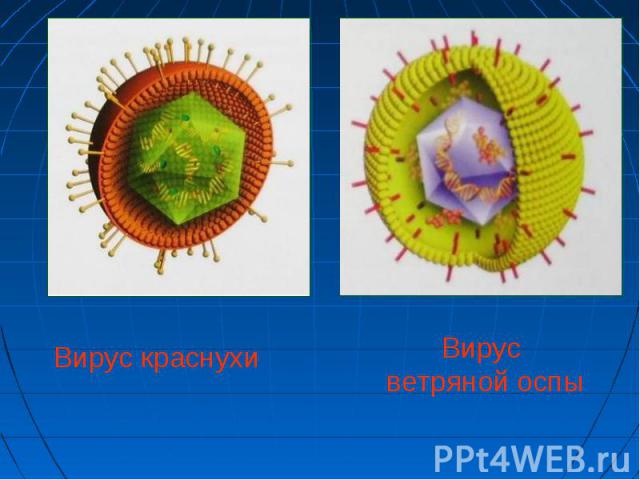
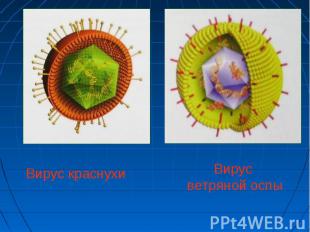
Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр.

Вы узнали о многогранниках все что мы смогли вам показать=) Вы узнали о многогранниках все что мы смогли вам показать=)