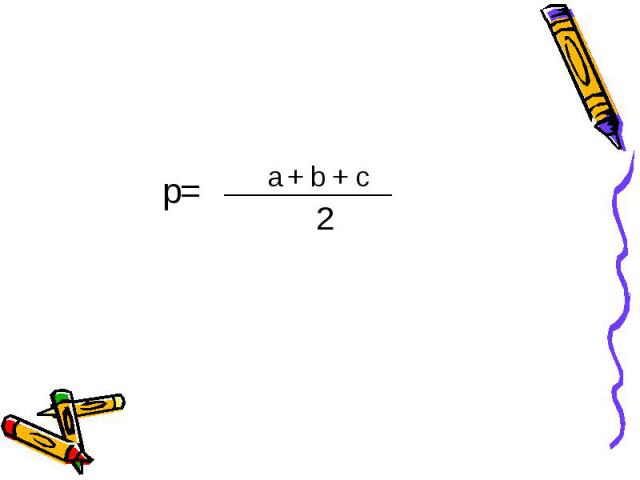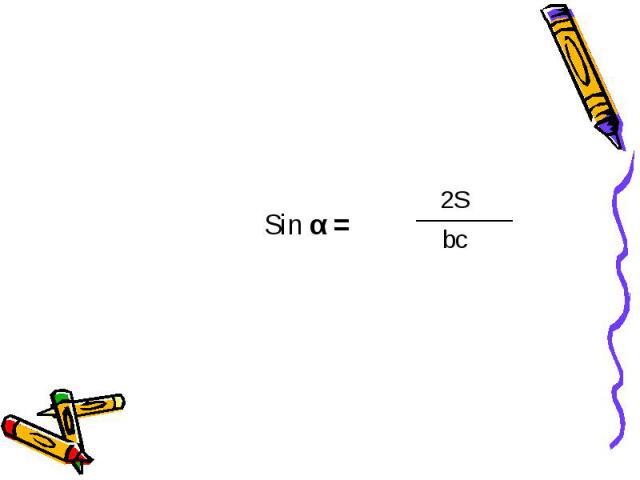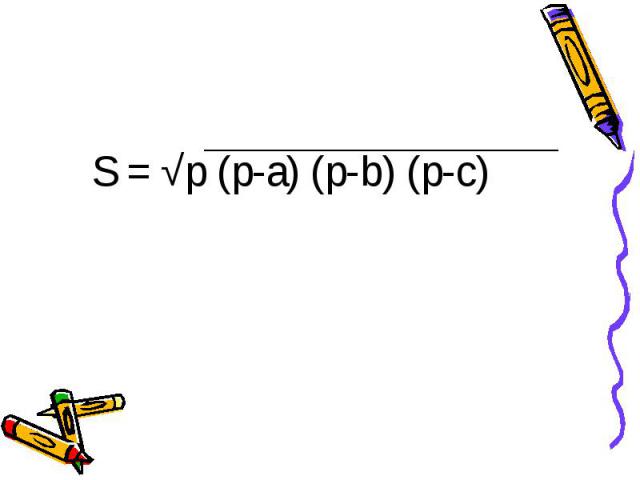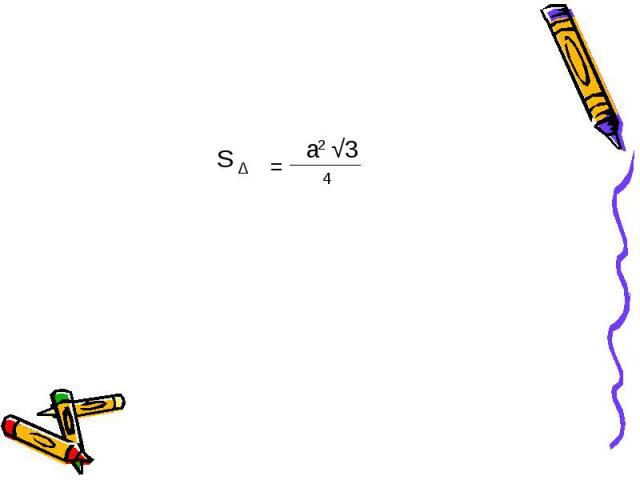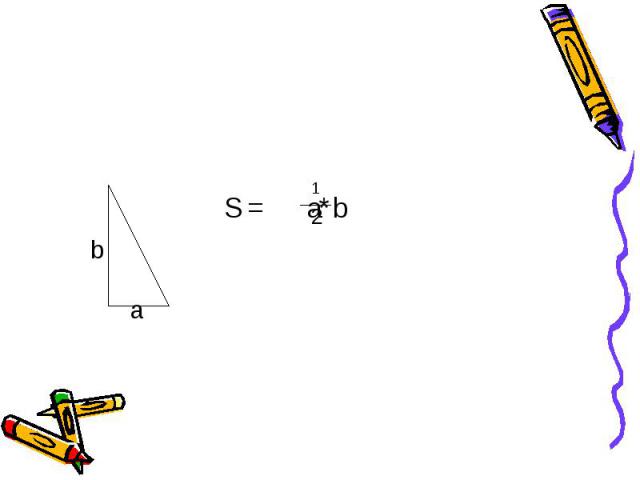Презентация на тему: Формулы для вычисления площади треугольника

Открытый урок по геометрии в 9 классе. Тема: «Формулы для вычисления площади треугольника» Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.

Цель урока: Познакомится с формулами для вычисления площадей треугольника: а) по стороне и высоте, проведенной к этой стороне; б) по двум сторонам и углу между ними; в) формулой Герона г ) Через радиус вписанной окружности и описанной окружности

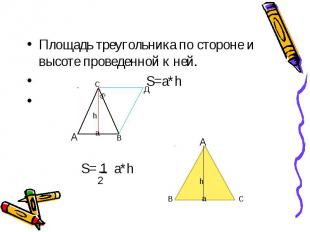
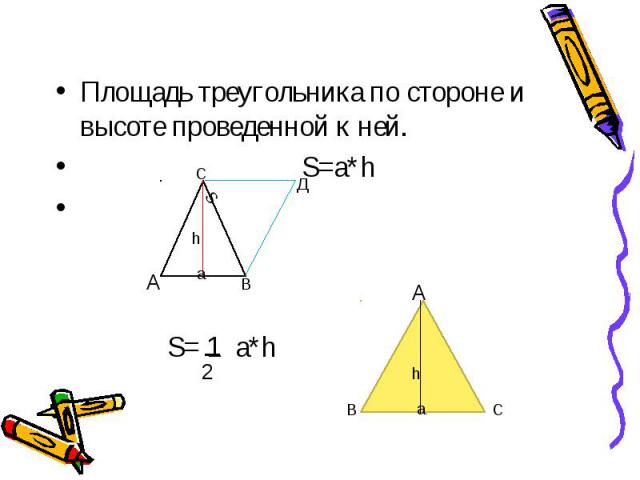
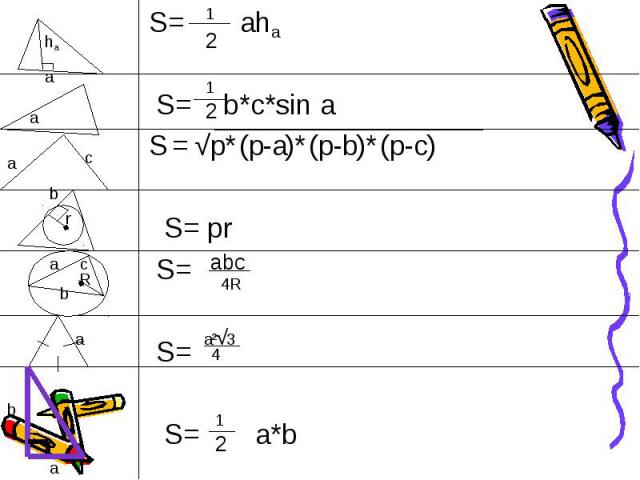
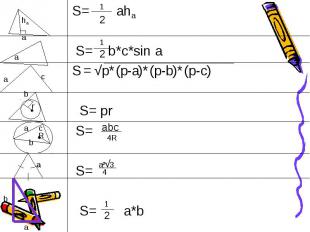
Площадь треугольника по стороне и высоте проведенной к ней. S=a*h

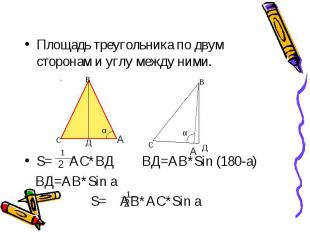
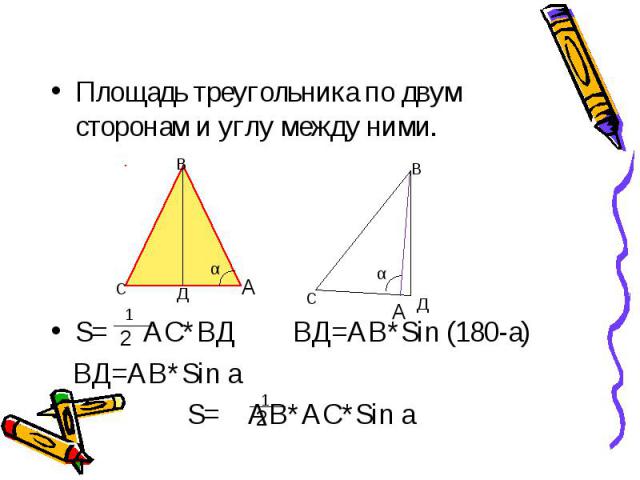
Площадь треугольника по двум сторонам и углу между ними. S= АС*ВД ВД=АВ*Sin (180-a) ВД=АВ*Sin a S= АВ*АС*Sin a

Древнегреческий математик Герон Александрийский (I в. н.э.) Получил формулу для вычисления площади треугольника по его трём сторонам: S = √p (p-a) (p-b) (p-c)

Краткий вывод формулы Герона

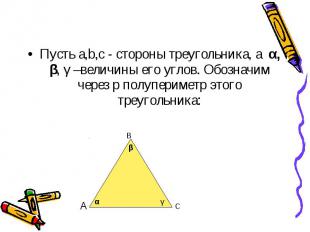
Пусть a,b,c - стороны треугольника, а α, β, γ –величины его углов. Обозначим через p полупериметр этого треугольника:

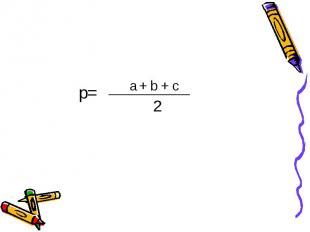
По теореме косинусов : cos α=

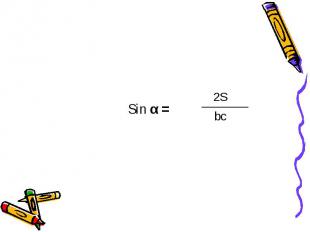
Sin α =

Подставляя найденные выражения Sin α и Cos α в формулу Sin² α + Cos² α = 1, получим:

Отсюда, применяя формулу разности квадратов, имеем: p ( p – a )( p – b )( p - c)

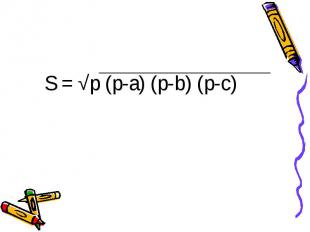
S = √p (p-a) (p-b) (p-c)

Дано: АВС –треугольник АВ=ВС=АС=а Вывести:формулу площади треугольника S = a*h h= √ - =a √3 S= * a* a √3

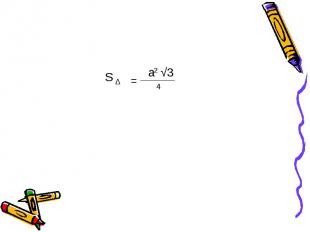
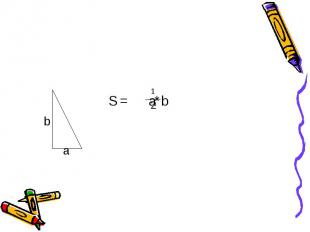
S = a*b

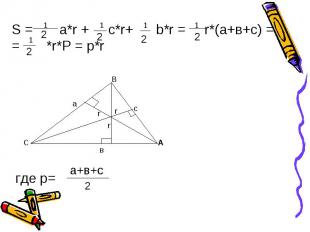
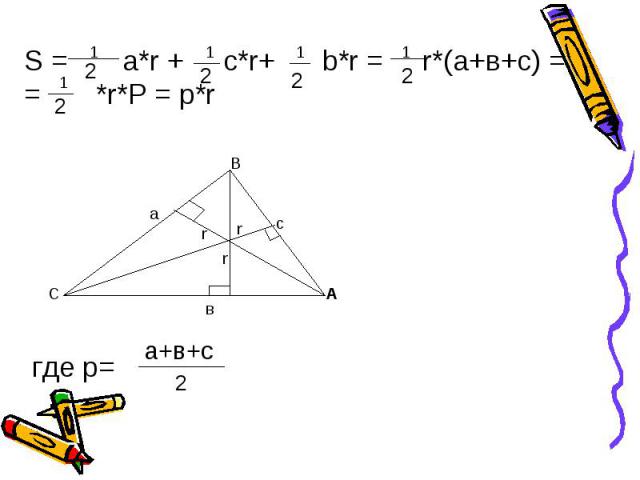
S = a*r + c*r+ b*r = r*(а+в+с) = = *r*Р = р*r где p=

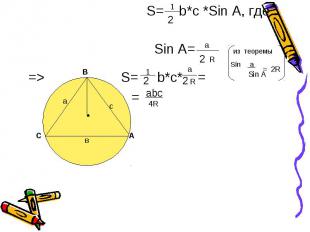
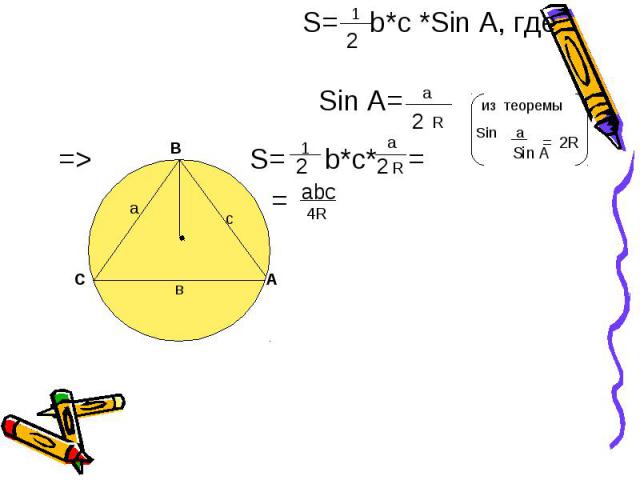
S= b*с *Sin А, где Sin A= из теоремы Sin a => S= b*с* = =

Закрепление

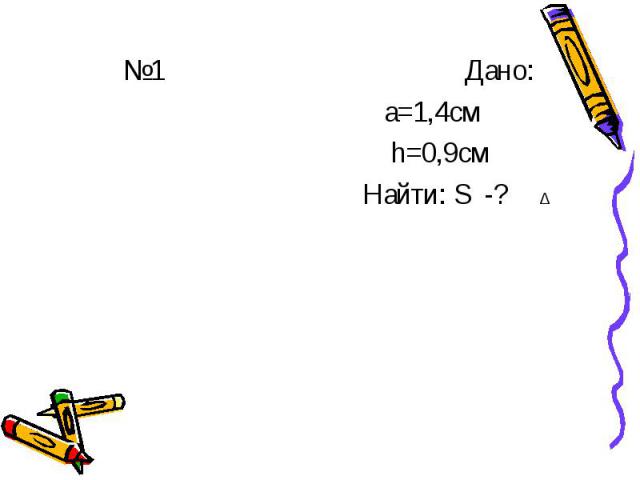
№1 Дано: а=1,4см h=0,9см Найти: S -?

№2 Дано: а=5см b=6см α = зо

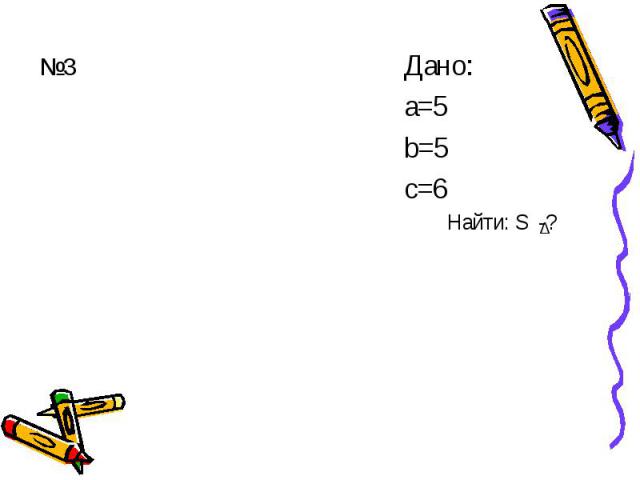
№3 Дано: а=5 b=5 с=6

Д/ З: п.124,125 №30(1), №27