Презентация на тему: Формулы приведения

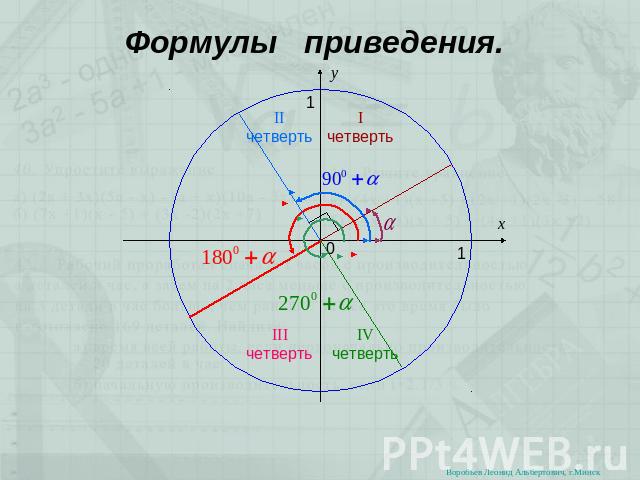
Формулы приведения.
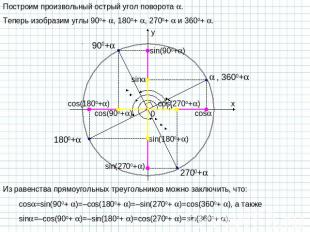
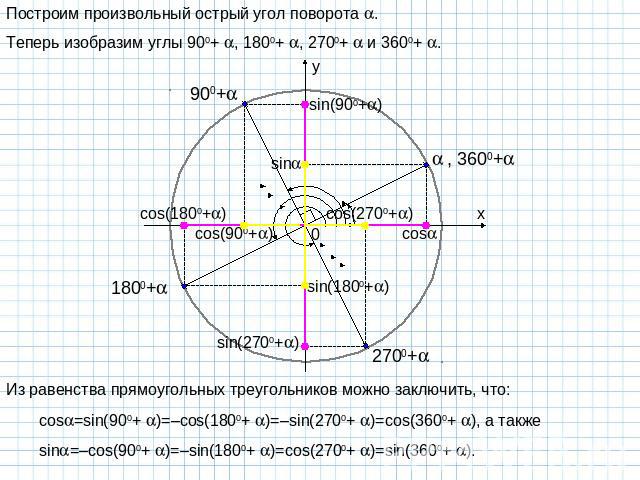
Построим произвольный острый угол поворота . Теперь изобразим углы 900+ , 1800+ , 2700+ и 3600+ . Из равенства прямоугольных треугольников можно заключить, что: cos=sin(900+ )=–cos(1800+ )=–sin(2700+ )=cos(3600+ ), а также sin=–cos(900+ )=–sin(1800+ )=cos(2700+ )=sin(3600+ ).

Значения тригонометрических функций любых углов поворота можно привести к значению тригонометрических функций острого угла. Для этого и применяются формулы приведения. Попробуем разобраться в следующей таблице (перенесите её в тетрадь!): С первым столбцом все ясно – в нем известные Вам тригонометрические функции. Во втором столбце показано, что любой аргумент(угол) этих функций можно представить в таком виде. Поясним это на конкретных примерах:

Умножьте полученные сумму или разность на и получите искомые выражения. Как видите мы использовали известное Вам с начальной школы действие – деление с остатком. Причем, остаток не превышает делителя 90 (в случае градусной меры) или (в случае радианной меры). Потренируйтесь делать это! В любом случае мы добились следующего: наш аргумент тригонометрической функции представлен в виде целого числа прямых углов плюс или минус какой-то острый угол. Обратим теперь внимание на 3-й и 4-й столбцы таблицы. Сразу заметим, что в случае четного числа прямых углов тригонометрическая функция остается такой же, а в случае нечетного числа – изменяется на кофункцию (sin на cos, tg на ctg и наоборот), причем аргументом этой функции является остаток.
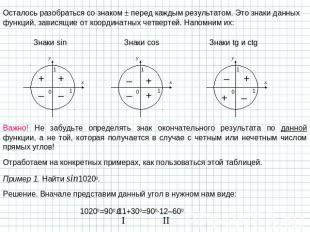
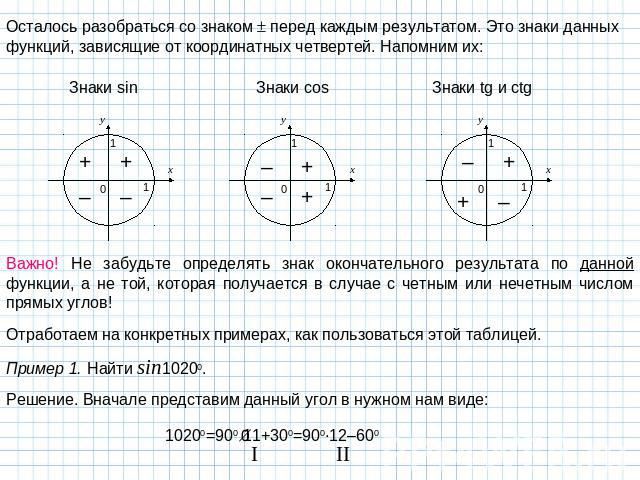
Осталось разобраться со знаком перед каждым результатом. Это знаки данных функций, зависящие от координатных четвертей. Напомним их: Важно! Не забудьте определять знак окончательного результата по данной функции, а не той, которая получается в случае с четным или нечетным числом прямых углов! Отработаем на конкретных примерах, как пользоваться этой таблицей. Пример 1. Найти sin10200. Решение. Вначале представим данный угол в нужном нам виде:
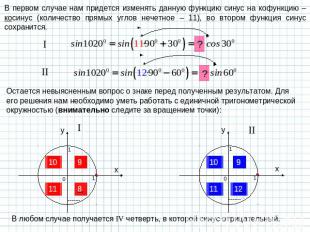
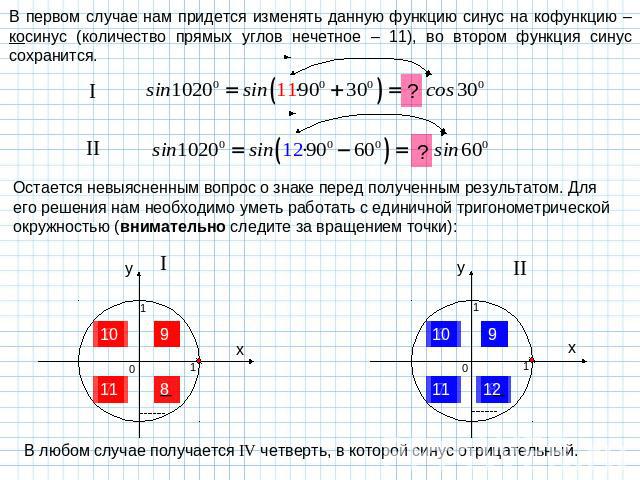
В первом случае нам придется изменять данную функцию синус на кофункцию – косинус (количество прямых углов нечетное – 11), во втором функция синус сохранится. Остается невыясненным вопрос о знаке перед полученным результатом. Для его решения нам необходимо уметь работать с единичной тригонометрической окружностью (внимательно следите за вращением точки): В любом случае получается IV четверть, в которой синус отрицательный.

Пример 2. Все этапы решения проделайте самостоятельно (под контролем учителя). В случаях, когда аргумент тригонометрической функции является отрицательным, используют свойства четности и нечетности тригонометрических функций:

Пример 3. Привести к значению тригонометрической функции положительного острого угла значение tg(–20000). Т.к. формулы приведения приводят к значению тригонометрических функций острого угла, то достаточно держать в памяти: